矩陣方程AXB+CXT D=E 自反最佳逼近解的迭代算法
楊家穩(wěn)
(滁州職業(yè)技術(shù)學(xué)院 基礎(chǔ)部,安徽 滁州 239000)
0 引言
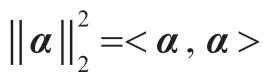
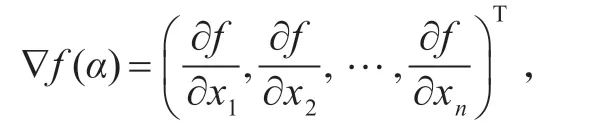

本文考慮如下問(wèn)題:
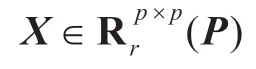
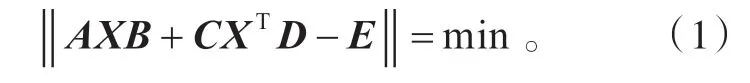
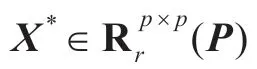
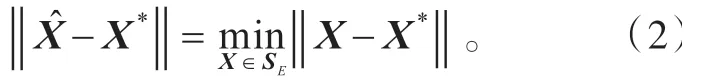
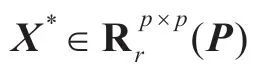
關(guān)于反射矩陣的自反矩陣或反自反矩陣在系統(tǒng)與控制理論、工程、科學(xué)計(jì)算等領(lǐng)域都有廣泛的應(yīng)用[1-2]。近年來(lái),Sylvester 矩陣方程是計(jì)算數(shù)學(xué)研究的熱點(diǎn)之一,并且取得很多成果。若矩陣方程是相容的,文獻(xiàn)[3]利用廣義Moore-Penrose給出了AX+XTC=B 解的表達(dá)式,文獻(xiàn)[4-5]用共軛梯度迭代算法給出矩陣方程AXB+CXTD=E 極小范數(shù)最小二乘解,文獻(xiàn)[6]給出了XA+AXT=0 的一般解,文獻(xiàn)[7]給出AXB+CXTD=E 的可解性,文獻(xiàn)[8]給出求解方程A1X1B1=C 、A2X2B2=D 的自反(或反自反)的最佳逼近解。若矩陣方程是不相容的,對(duì)于任意給定矩陣,文獻(xiàn)[9]提出一種算法求ATXB+BTXTA=D 的最佳逼近解,文獻(xiàn)[10]提出一種算法求AXB+CXD=E 自反(或反自反)的最佳逼近解。
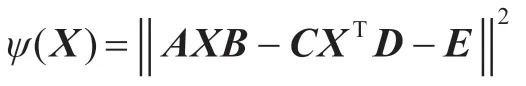
1 迭代算法
本節(jié)首先給出解決問(wèn)題Ⅰ和Ⅱ的迭代算法,然后證明該算法收斂,最后研究如何計(jì)算到非空凸集K 上的投影。具體算法步驟如下:
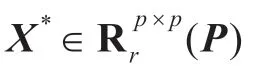
步驟2 計(jì)算
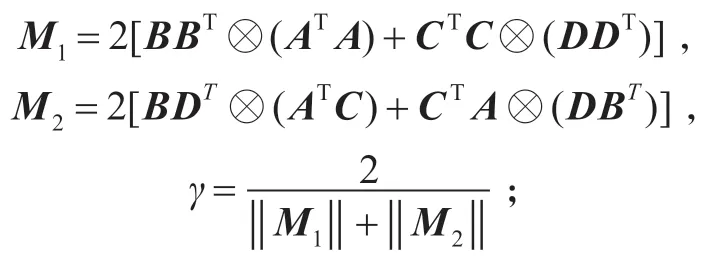
步驟3
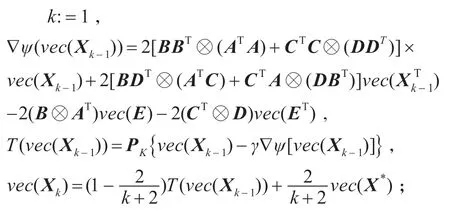
步驟4 若‖Xk-Xk-1‖<ε ,則停止;否則,k:=k+1,轉(zhuǎn)向步驟3。
為了證明算法的收斂性,首先給出下面的定義和定理。
定義1 若?x1,x2∈S ?H ,?κ >0 ,使得‖T(x)-T(y) ‖≤κ‖x-y ‖成立,則映射T:H →H稱為κ-Lipschitzian(或κ-Lipschitzian 連續(xù))。特別地,若對(duì)于一切x,y ∈H ,有‖T(x)-T(y) ‖≤‖x-y ‖成立,則映射T:H →H 稱為非擴(kuò)展映射。
定義2 對(duì)于給定的集合S ?H ,若?x,y ∈S,?η >0 ,使F(x)-F(y),x-y ≥η‖x-y‖2成立,則稱映射F:H →H 在集合S 上η 強(qiáng)單調(diào)。
定理1[11](HSDM)設(shè)T:H →H 是非擴(kuò)展映射,且Fix(T)≠?。又設(shè)函數(shù)θ:H →R ∪∞存在Gateaux 導(dǎo)數(shù)θ′:H →H ,且θ′ 在T(H) 上滿足κ-Lipschitzian ,且η 強(qiáng)單調(diào)。對(duì)于任意的u0∈H和正實(shí)數(shù)序列(λn)n≥1滿足:
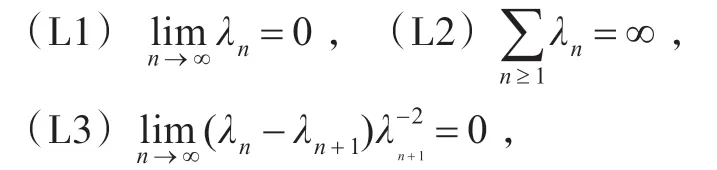
或者
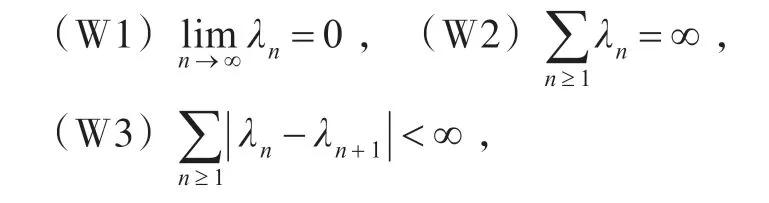
則由
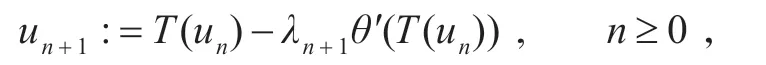
生成的序列(un)n≥0強(qiáng)收斂于唯一的u*,其中u*滿足θ(u*)=inf{θ(Fix(T))} 。
定理2[12]設(shè)K ?H 是閉凸子集,又設(shè):
(i)ψ:H →R ∪{ }∞ 是Gateaux 可微的凸函數(shù)且 它 的 導(dǎo) 數(shù) ψ′:H →H 在 H 上 滿 足γ-Lipschitzian,
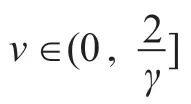
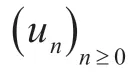
引理1 設(shè)ψ(νec(X))=‖AXB+CXTD-E‖2,則有
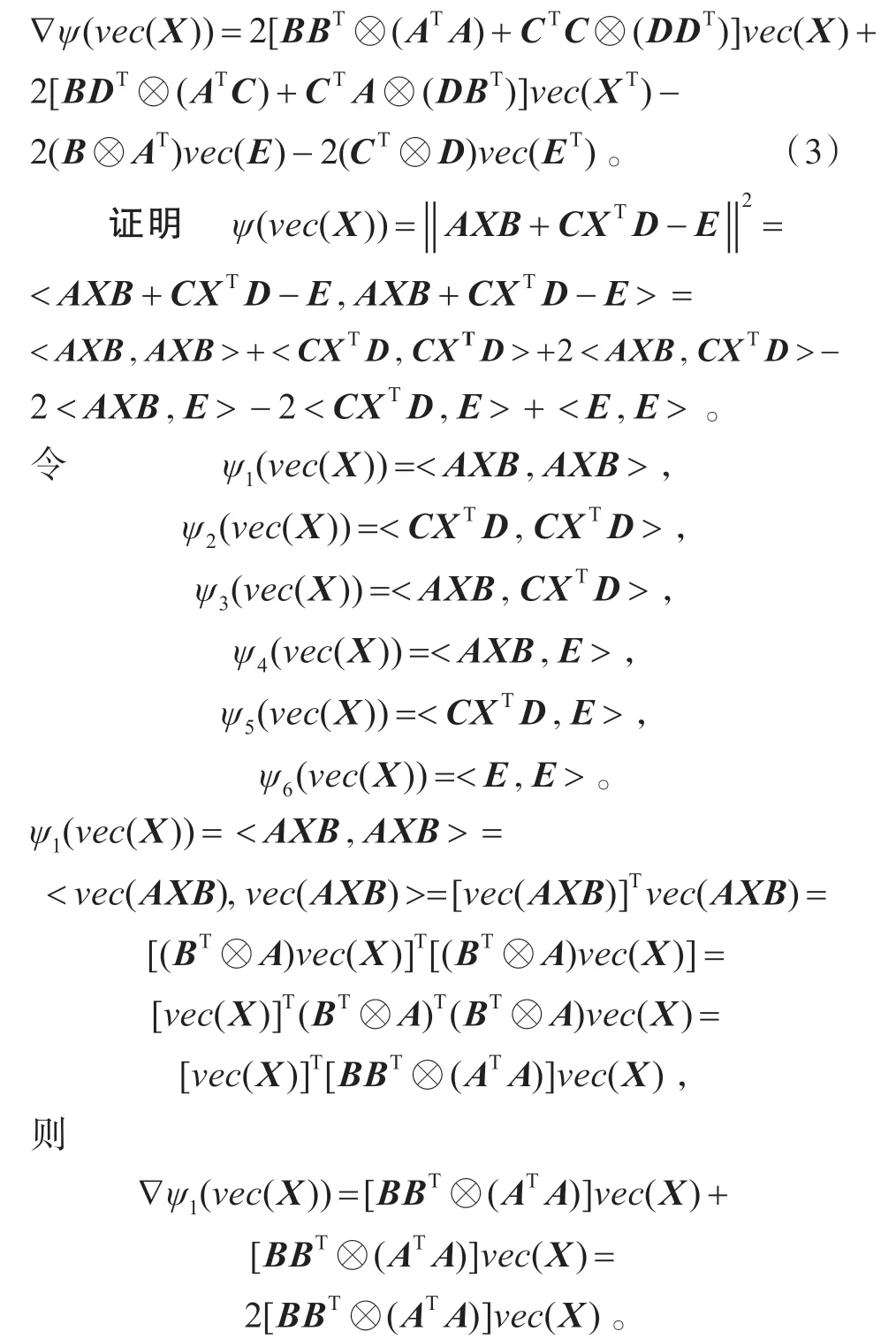
同理,可得
▽?duì)?(νec(XT))=2[DDT?(CTC)]νec(XT),
所以▽?duì)?(νec(X))=2[CTC ?(DDT)]νec(X)。
依次計(jì)算可得
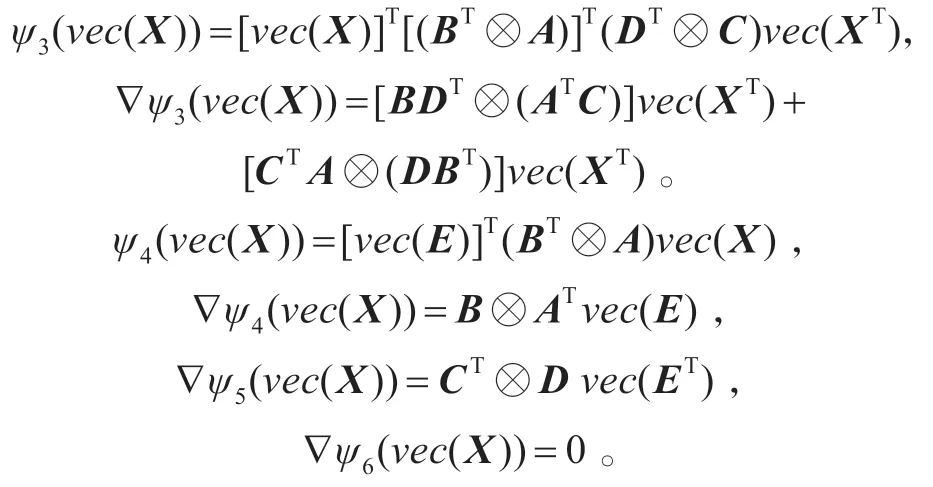
則(3)式得證。
引理2 設(shè)θ(νec(X))=‖‖X-X*2,則
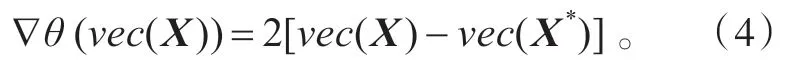
證明 θ(νec(X))=‖‖X-X*2=<X-X*,X-X*>= <νec(X-X*),νec(X-X*)>=[νec(X-X*)]T[νec(X-X*)]。
則(4)式得證。
可以證得:
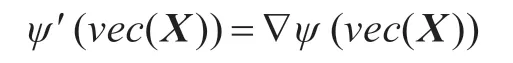
和
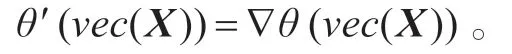
因此,分別用▽?duì)?νec(X)) 和▽?duì)?νec(X)) 來(lái)代替ψ′(νec(X))和θ′(νec(X))。
引理3 設(shè)ψ(νec(X))=‖AXB+CXTD-E‖2,θ(νec(X))=‖‖X-X*2,則有如下結(jié)論:
(a)ψ(νec(X))是凸函數(shù);
(b)θ(νec(X))是凸函數(shù);
(c)▽?duì)?νec(X))是γ-Lipschitizian;
(d)▽?duì)?νec(X))是κ-Lipschitzian;
(e)▽?duì)?νec(X))是η 強(qiáng)單調(diào)的。
證明 由凸函數(shù)的定義,可以證明(a)、(b)成立。
(c)令
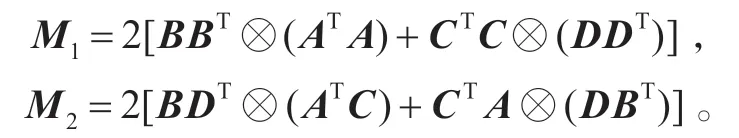
根據(jù)(3)式有

因此,▽?duì)?νec(X)) 是γ-Lipschitizian ,其中γ=‖ ‖M1+‖ ‖M2。
(d)由(4)式有
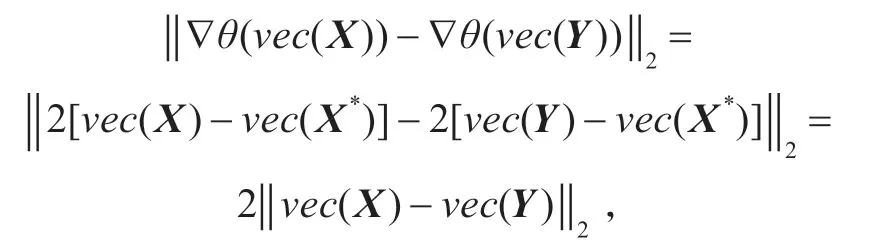
因此,▽?duì)?νec(X)) 是κ-Lipschitzian ,其中κ=2。
(e)由(4)式可以得到
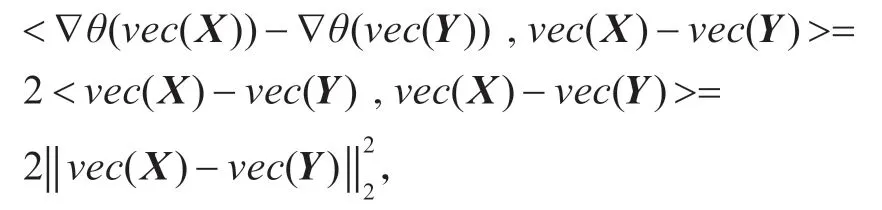
根據(jù)定義2,可以推出▽?duì)?νec(X)) 是η 強(qiáng)單調(diào)的,其中η=2。
證明由引理1 ~3 可知,ψ(νec(X)) 和θ(νec(X))滿足定理2 的條件,由定理2 可以推出算法是收斂的。
在算法中需要計(jì)算到凸集K 上的投影。為此給出如下定理:
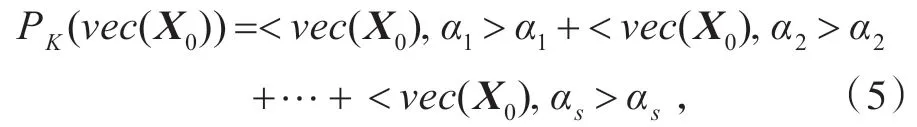
其中,α1,α2,…,αs是矩陣(I-PT?P) 零空間的標(biāo)準(zhǔn)正交基。
證明 由自反矩陣的定義有

(7)式改寫(xiě)成
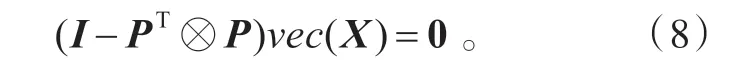
凸集K 中的元素就是線性方程(8)的解。因此只要給定(8)式解集合的標(biāo)準(zhǔn)正交基,就可以利用(5)式計(jì)算出νec(X0)在K 上的投影。
2 數(shù)值舉例
下面用兩個(gè)數(shù)值例子來(lái)驗(yàn)證上述算法的可行性,所有實(shí)驗(yàn)都在MATLAB2007R 中進(jìn)行。
例1 考慮矩陣方程AXB+CXTD=E,其中
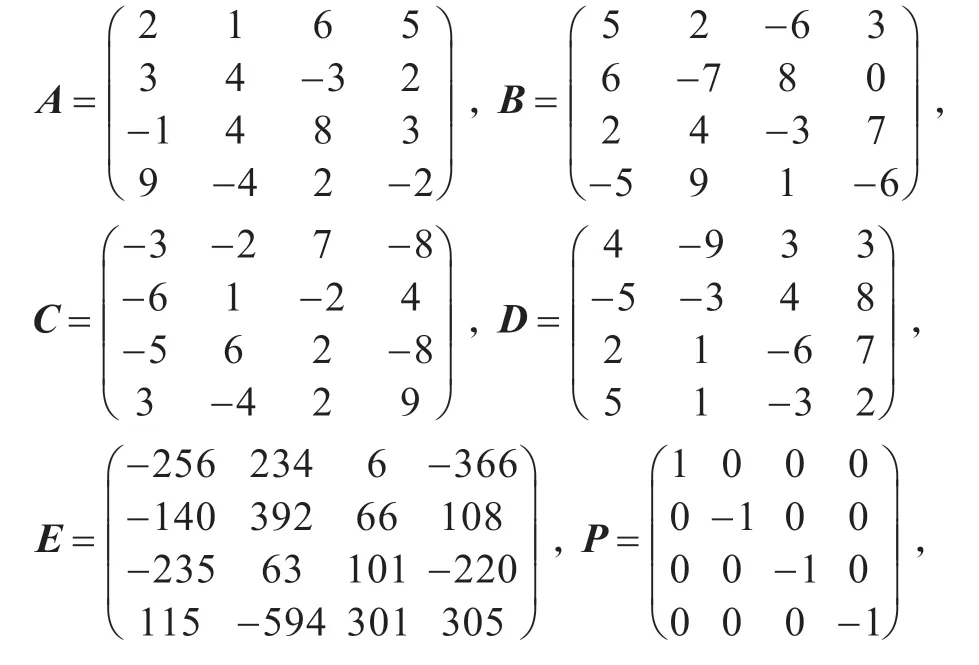

是矩陣方程相容的解。
利用算法,令ε=1.0e-11,可得
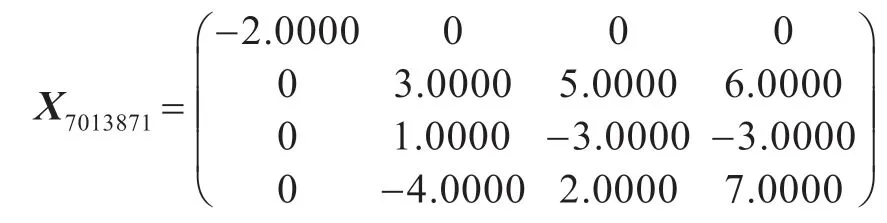
相應(yīng)的余項(xiàng)為
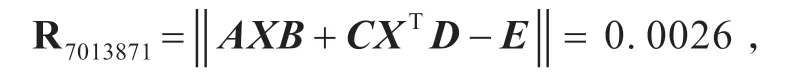
例2 仍然考慮矩陣方程AXB+CXTD=E ,其中A,B,C ,D,P 和X0同例1,
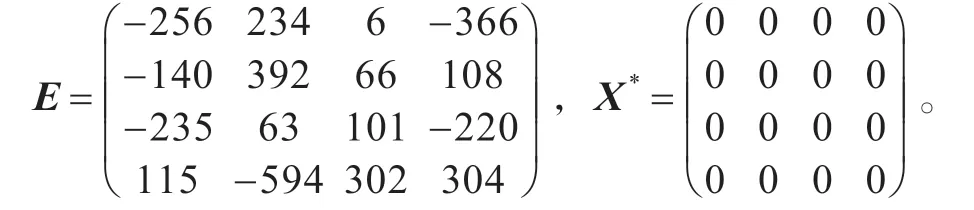
可以證明上述矩陣方程是不相容的。令ε=1.0e-10,由算法得
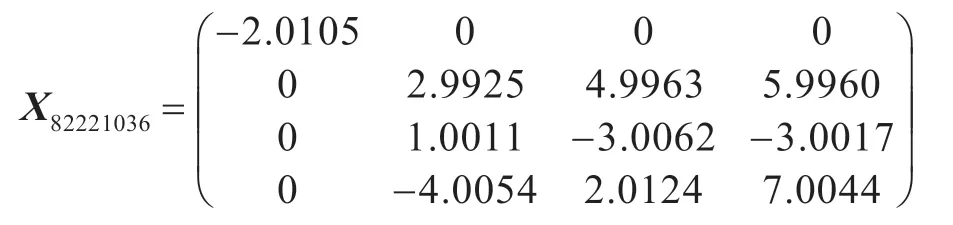
相應(yīng)的余項(xiàng)
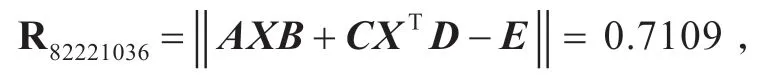
3 結(jié)語(yǔ)
本文利用HSDM,給出求解矩陣方程AXB+CXTD=E 自反(或反自反)最佳逼近解的迭代算法。無(wú)論方程AXB+CXTD=E 是否相容,所給的算法都可以計(jì)算其自反(或反自反)的最佳逼近解。實(shí)例說(shuō)明了算法的可行性,但該算法的缺點(diǎn)是收斂速度較慢。文中自反(或反自反)矩陣的集合是凸集。若其他矩陣方程的未知約束矩陣是凸集,則可以應(yīng)用HSDM 解決其最佳逼近問(wèn)題。
[1] Chen H C.Generalized reflexive matrices:special properties and applications[J]. SIAM J Matrix Anal Appl,1998,19(1):140-153.
[2] Chen H C. The SAS domain decomposition method for structural analysis[R]. Urbana:University of Illinois,1988.
[3] Piao F X,Zhang Q L,Wang Z F. The solution to matrix equation AX+XTC=B[J]. Journal of the Franklin Institute,2007,344:1056-1062.
[4] Xie L,Liu Y J,Yang H Z. Gradient based and least squares based iterative algorithms for matrix equation AXB+CXTD=E[J]. Applied Mathematics and Computation,2010,217:2191-2199.
[5] Wang M H,Cheng X H,Wei M S. Iterative algorithms for solving the matrix equation AXB+CXTD=E[J].Applied Mathematics and Computation,2007,187(2):622-629.
[6] Teran F,Dopico F. The solution of the equation XA+AXT=0 and its applications to the theory of orbits[J].Linear Algebra Appl,2011,434:44-67.
[7] 趙琳琳. 矩陣方程AXB+CXTD=E 的可解性[J]. 山東大學(xué)學(xué)報(bào):理學(xué)版,2012,47(10):45-48.
[8] Dehghan M,Hajarian M. Finite iterative algorithms for the reflexive and anti-reflexive solutions of the matrix equations A1X1B1=C,A2X2B2=D[J]. Mathematical and Computer Modeling,2009,49:1937-1959.
[9] 盛興平,蘇友峰,陳果良. 矩陣方程ATXB+BTXTA=D 的極小范數(shù)最小二乘解的迭代算法[J]. 高等學(xué)校計(jì)算數(shù)學(xué)學(xué)報(bào),2008,30(4):352-362.
[10]孫合明,李慶芳,楊家穩(wěn). 自反矩陣下矩陣方程AXB+CXD=E 的最佳逼近解[J]. 重慶理工大學(xué)學(xué)報(bào):自然科學(xué),2012,26(4):109-114.
[11]Yamada I. The hybrid steepest descent method for the variational inequality problem over the intersection of fixed point sets of nonexpansive mappings[M]//Butnariu D,Censor Y,Reich S. Inherently parallel algorithm for feasibility and optimization and their applications.Amsterdam:Elsevier,2001:473-504.
[12]Yamada I,Ogura N,Shirakawa N. A numerically robust hybrid steepest descent method for the convexly constrained generalized inverse problems[J]. Contemporary Mathematics,2002,313:269-305.

