壟斷者跨時利潤和最優化模型與科斯猜想

余 敏 上海市普陀區業余大學

近幾十年，博弈論不斷加速向現代經濟學滲透。羅納德·科斯（ronald coase）提出一種觀點，認為在某些條件下，經濟的外部性或曰非效率可以通過當事人的談判而得到糾正。“科斯猜想”（Coase Conjecture）是科斯在1972年發表的《Durability and Monopoly》論文中所做的一個猜測。科斯教授提出，由于將來銷售的耐用品將會影響到現在所售出的產品的未來價值，在壟斷耐用品生產者沒有對未來的產量水平做出承諾時，如果消費者具有價格下跌的理性預期，那么壟斷價格就會迅速降到邊際成本水平。這個觀點源于一系列案例，科斯本人一直拒絕把他初始論文中的論點加以廣泛地推廣，因此對于他論文中的每一個解釋，出現另外多種似乎說得通的看法。以下通過討論壟斷者跨時利潤和最優化模型進行提示性證明。

一、壟斷者的跨時利潤

假設1 單位生產成本為0，（此假設只是為了討論的方便）。

假設2 壟斷者和消費者無限地活著。

假設3 消費者的估價ν 均勻地分布在[0，1/（1-δ）]上。（相當于每階段估價均勻地分布在[0，1]上）

假設4 估價為ν 的消費者效用δt（ν-Pt），Pt表示t

假設5 “穩態假設”：當某一時間面對價格P時，任何估價超過ω（P）=λ P的消費者將購買，估價較低的消費者不會購買，其中λ>1。反之，如果在某一時間估價超過ν 的消費者買了，而其他的消費者沒有購買，壟斷者要價P（ν）=μν，其中μ<1

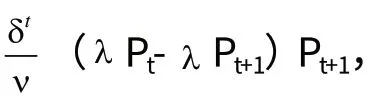
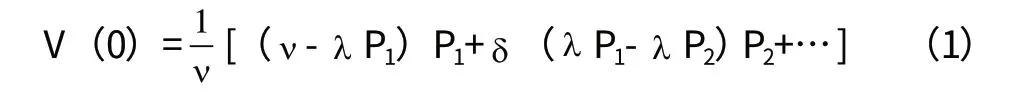
其中ν>λ P1>λ P2>…

引理1 證明壟斷者對Pt的最優化導致一種線性規劃，其中λ 作為μ 的函數由下式給 1-2 λμ+δ λ2μ2=0

[證明] 對（1）式中的P1求導令其為0，得

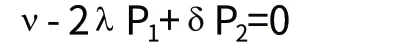
由于 P1=μν，P2=μ（λ P1）= λ μ2ν，即得

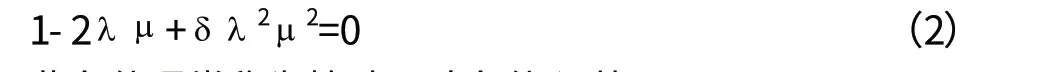
此條件通常稱為檢驗二階條件 證畢

引理2 消費者ω（P）的無差異方程

[證明] 估價為λ P的買方現在就買和等待下一個階段買之間是無差異的，即

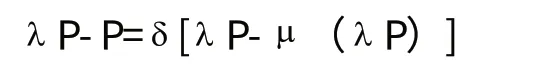
兩端去掉P即得（3） 證畢

引理3 當δ →1時，壟斷者的利潤趨于0

[證明] 由（2）與（3）解得

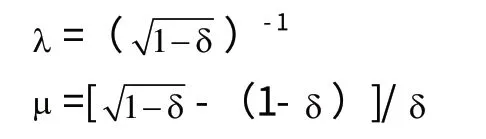
由此得1lim

δ→μ=0 證畢

此引理的實際意義為，當消費者的貼現函數接近于1時，則有充分大耐心來等待，以使得消費者支付獲得最大，這樣就迫使壟斷者以邊際成本來定價，從而利潤趨于0。

假設7 壟斷者承諾價格順序（P1，P2，P3，…）

引理4 證明在尋找最優價格政策時，壟斷者約束自己于價格序列（單調減少）P1≥ P2≥ P3≥…

[證明] 對某些正的K，價格Pt≥Pt-k將不被任何消費者接受，因為消費者會以低價Pt-k購買，并較早地享用該商品，因此，選擇Pt=min

k（Pt-k）導致同樣的結果。

二、最優化模型

由引理2.估價為ν 的消費者在接受Pt和等待Pt+1之間無差異

當且僅當 （ν-Pt）=δ（ν-Pt+1） 及（1）式，得

壟斷者的最優化問題為：

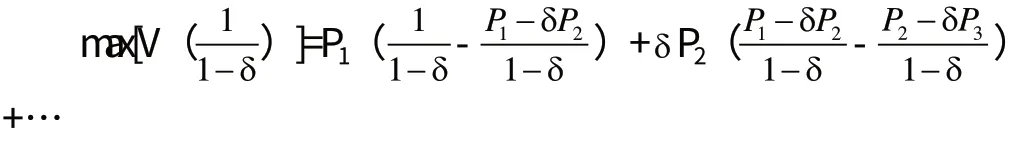
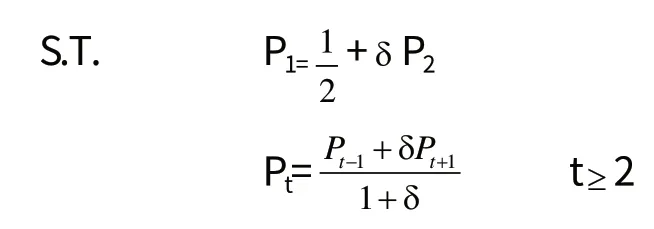
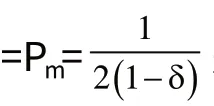
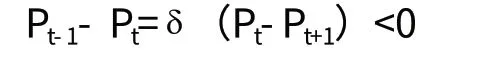
代入目標函數可得

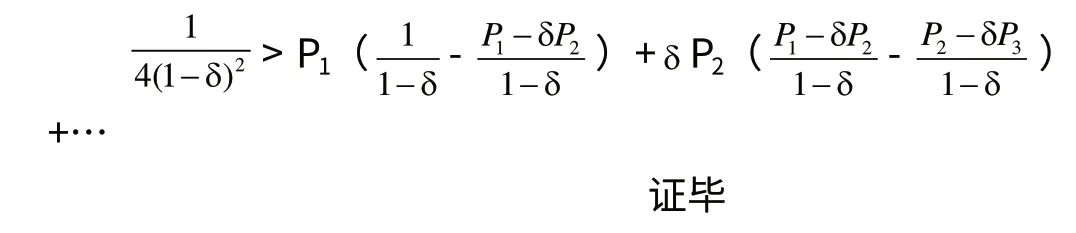
三、科斯猜想的提示性證明

科斯在耐用品和跨時價格歧視的極端情況下猜想：當價格調整的間隙收斂為零時，一個無限耐用品的生產者損失了他的全部壟斷力量。

證明：考察無限時序t=1，2，…。對于壟斷者的要價序列{P1，P2，……Pt-1}，賣方在t期開始時的后驗信念，是在[0，bt]區間估價為某一b的買方還沒有購買商品，而在（bt，+∞）區間估價為b的買方已經以某一bt購買時的信念，即壟斷者的后驗信念一定要與他的裁剪的先驗信念相一致。

假設買方遵從一種簡單的“穩態的”策略：即在t期要價Pt時估價超過 β（Pt）的買方購買，而估價低于β（Pt）的買方不購買，其中β（·）是遞增函數，且對所有的Pt>0，β（Pt）> Pt

為了簡化起見，令C=O壟斷者的邊際成本，F（b）代表在[0，+∞]的買方估價的積累分布（對b>0，有F（0）=0，F（b）>0，F（+∞）=1）最后取貼現因子δ=exp（-γ·△），其中△是階段之間的實際時長，γ>0，顯然我們對△趨于0時所發發生的事情感興趣。

由于買方策略的穩定性，壟斷者自一給定期t開始的利潤的當前貼現價值，取決于剩余買方的分布。令V（bt）代表貼現利潤，顯然V（·）是非遞增函數，令Ft≡F（bt）代表t期前還沒有購買的買方比例。

固定真實時間ε>0，令△收斂于0，對任意η>0，存在著一個充分小的△和t，使得（t+2）·△<ε，滿足

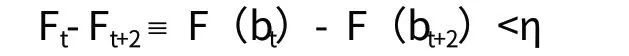
由于0-ε之間的階段數趨于無窮，我們總能發現兩個連續的階段使得在這些階段銷售的總數是由一定數值限定的。

如果從真實時間ε起的利潤V（bε/Δ）是不可忽略的，壟斷者就會有積極性通過快一點削價加速此過程，因此，來自歧視的收益是二階的，而通過在t期作出計劃在t+1期作出的提供，壟斷者會通過一個階段加速此過程，并且獲得一階收益（對△），如果V（bε/Δ）不是很小的話

下面寫出壟斷者寧可在t期要價Pt，在t+1期要價Pt+1而不是直接在t期要價Pt+1，情況下的條件：

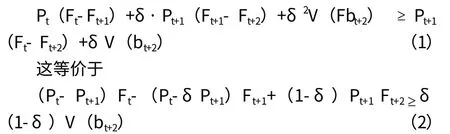
根據bt+1定義，估價bt+1的買方在接受Pt和接受Pt+1之間是不在意的，因此

即Pt-δPt+1=（1-δ）bt+1

代入（1），并用（1-δ）除，得

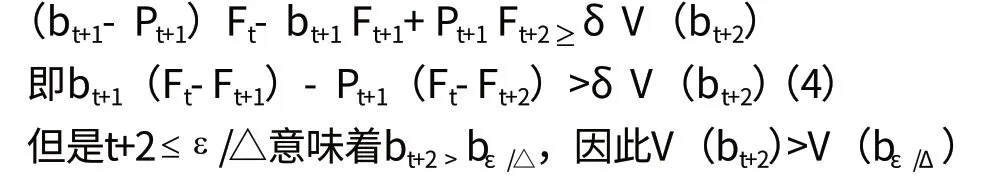
還有Ft+1> Ft+2，因此（4）式可寫成

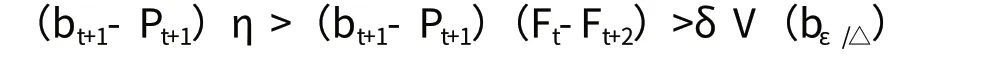
這意味著通過選擇充分小的η，能夠使賣方自真實時間起的貼現利潤值任意小，因此通過選擇足夠小的△，使自任何時間（包括趨近于0的時間）起的貼現利潤值任意小。

科斯定理是現代產權經濟學關于產權安排、交易費用與資源配置之間關系的思想的集中體現，也是現代產權經濟學的基本核心內容，全面、準確地把握科斯定理的含義，對于深化我國國有企業改革，建立現代企業制度具有一定的借鑒意義。

[1]張維迎.《博弈論與信息經濟學》.上海人民出版社

[2][美] Drew.Fudenberg，[法]Jean.Tirole.《博弈論》.中國人民出版社

[3][瑞典] W.W eibull.《演化博弈論》.上海三聯書店、上海人民出版社，2006.3