輥式板材矯正機壓下量計算

曹益忠

（太原重工股份有限公司，山西 太原 030024）

0 引言

輥式板材矯正機是目前應用最廣的矯正金屬板材的一種矯正機，其矯正板材的過程在理論上都是用金屬的彈塑性純彎曲理論來解釋的。輥式板材矯正機需要設定合理的壓下量，才能夠獲得良好的矯正效果，有效消除殘余應力。本文利用金屬的彈塑性純彎曲理論，通過分析金屬板材在矯正過程中的彎曲模型，確定輥式矯正機的壓下量，進而為矯正機的合理調整提供有效指導。

1 板材彎曲變形與矯正

在輥式矯正過程中，板材通過上、下交錯布置轉動著的矯正輥時受到多次反復彎曲，在各輥之間板材產生不同程度的彎曲及彈復，矯正的實質就是要使板材產生適當反彎曲率的彎曲，以便在外負荷消除后，板材經彈復而變直［1］。板材在各矯正輥之間依次發生彈塑性變形，其初始板型缺陷在此過程中逐漸減小，直到平直。矯正過程及作用在板材上的彎矩示意圖如圖1所示。

2 板材彈塑性彎曲分析

金屬板材矯正過程中，在矯正力的作用下原始彎曲半徑為r0的板材向相反方向彎曲到矯正半徑ρ，如果用曲率表示其變形率ε，則有以下表達式：

其中：Z 為纖維距中性層的距離。

輥式板材矯正機主要是使金屬板材產生彈塑性彎曲變形，使板材得到矯正［2］。理想彈塑性材料在彈塑性變形時的應力分布如圖2所示。

由圖2可知：在Z0與中性層之間，應力小于板材屈服極限σs，纖維處于彈性變形狀態，屬于彈性變形區；在Z0與板材表層之間，應力等于屈服極限σs，纖維處于塑性變形狀態，屬于塑性變形區。因此Z0稱為彈塑性變形區高度，Z0處的纖維產生最大的彈性變形即彈性極限變形。根據虎克定律，Z0處的應變量εz0為：

其中：εs為應力等于屈服極限時的應變；E 為板材的彈性模量。

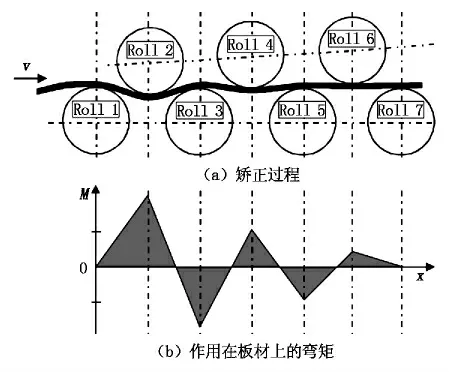
圖1 矯正過程及作用在板材上的彎矩示意圖

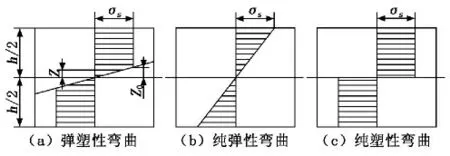
圖2 理想彈塑性材料應力分布圖

Z0處的應變εz0用式（1）的形式表示為：

由式（2）和式（3）可得出Z0與原始曲率和反彎曲率之間的關系式：

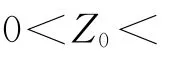
3 板材矯正機壓下量計算

在生產實踐中，常用塑性變形率λ 來衡量矯正效果，為了得到良好的矯正效果，不同厚度和材料的金屬板材在矯正過程中有不同的塑性變形率要求，一般塑性變形率λ 的范圍為：0＜λ＜90%［3］。塑性變形率λ與彈性變形區高度Z0的關系為：

將式（4）代入式（6）有：

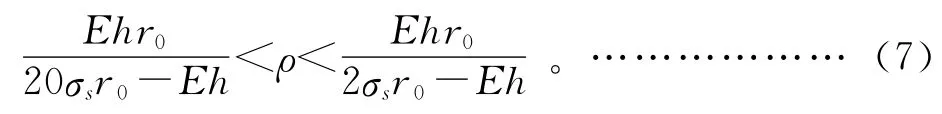
板材在矯正輥間的彎曲情形如圖3所示。

圖3 板材在矯正輥間的彎曲情形

圖3中，t為輥距，r為矯正輥半徑，h為板材厚度，ΔH 為壓下量（ΔH 的值可正可負），f 為板材在矯正過程的撓度。

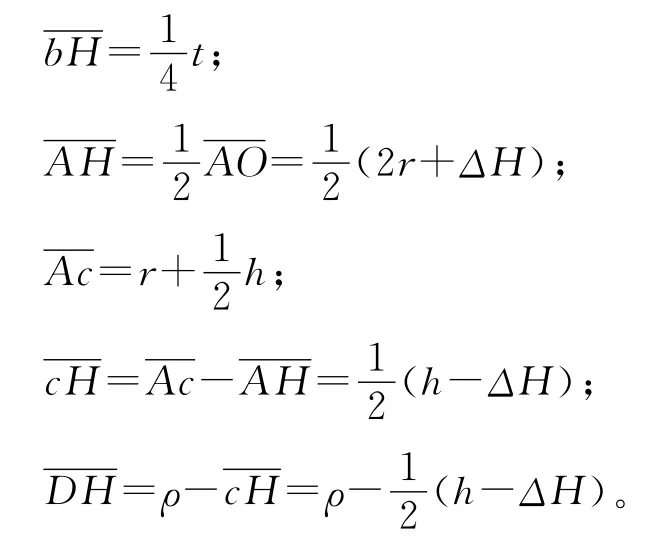
在三角形DbH 中，由勾股定理有：

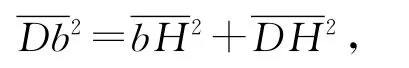
計算得：

將式（8）代入式（7），計算得：

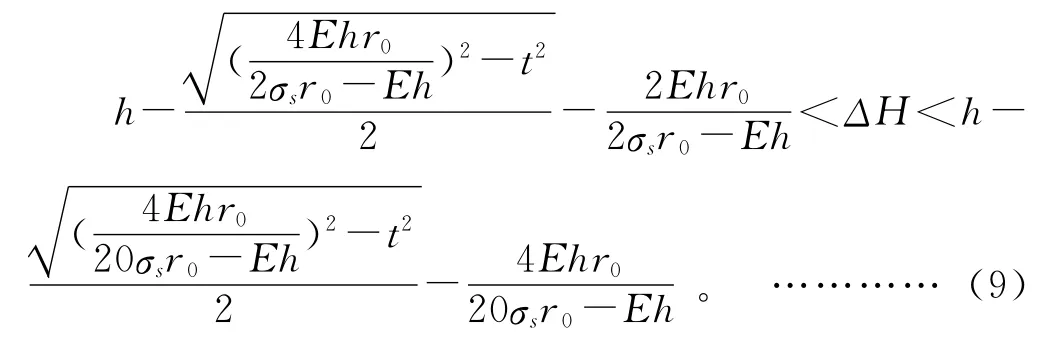
其中：r0為原始彎曲半徑，依據板厚及板形，取r0＝（10～30）h。

由式（9）可以得到一個矯正機壓下量的范圍，在實際矯正板材的過程中，只要壓下量設定在這個范圍內就能得到一定的矯正效果。

［1］ 崔甫.矯直原理與矯直機械［M］.北京：冶金工業出版社，2002.

［2］ 邊金生.軋鋼機械設備［M］.北京：冶金工業出版社，2003.

［3］ 王國棟.板形控制和板形理論［M］.北京：冶金工業出版社，1986.