身管直線度誤差對彈丸初速跳角散布的影響

米糧川，史玉彬，王鵬飛

（1.齊齊哈爾大學 機電工程學院，黑龍江 齊齊哈爾161006；2.63961部隊 復雜地面系統仿真重點實驗室，北京100012；3.中國兵器工業集團447廠 科研所，內蒙古 包頭104030）

由于火炮發射過程具有高溫高壓和瞬時性，火炮身管的制造誤差中炮膛的直線度誤差，或者稱身管的直線度誤差，以及由此產生的炮口角對火炮射擊精度的影響，長久以來是一個難以深入研究的難題。隨著科學技術的發展，特別是計算機技術的完善，絕大部分的設計工作和分析工作都可以在計算機上完成，計算機強大的信息容量和快速的數值解算能力，以及方便的人機交互性能為研究這一問題提供了新的條件和可能性。本文將研究的重點集中在采用計算機仿真技術探討身管直線度誤差對彈丸初速跳角散布的影響，制訂身管設計和制造的技術條件。研究策略：研究身管的形狀和炮口角導致的彈丸初速方向誤差，即跳角散布，只分析軸線在射面內的變化情況。身管為錐型體，仿真分析炮口指向同一方向，或立靶上的同一點，就如同實際工作中用瞄準具校炮一樣。內彈道計算采用經典模型，計算結果以炮膛壓力的形式引入仿真過程，仿真過程考慮了后坐運動和彈丸與身管的相對運動特性，包含了結構彈塑性的影響。材料有線彈性的，也有彈塑性的，使用DYNA3D分析各向異性材料的影響[1－3]。

1 炮膛軸線直線度的測量

火炮身管的制造過程包括毛胚的鍛造，內孔和外圓的粗加工，半精加工和精加工前的調質熱處理；身管校直機的校直工序、半精加工、時效處理；精加工和精加工之后的自緊等。這些工藝過程都不可避免地存在加工誤差，身管的金相組織結構中也會留下各種各樣的殘余應力，并且身管在火炮的裝配結構中處于嚴重的懸臂狀態，在炮身的自重作用下會產生彎曲變形，因此火炮身管的直線度和由此產生的炮口角是一個需要認真研究和精確測量的參數。身管直線度和炮口角的測量過去采用鉗工工作臺加千分表的測量方法，測量誤差比較大，并且與身管的實際使用工況不相符。本研究采用新研制的光電火炮內膛直線度測量系統，在火炮的實際工況中進行測量，測量結果比較可靠。某火炮炮膛軸線炮口角的測量結果如表1所示，表中，θ1為炮口角水平分量，θ2為炮口角的垂向分量，θ為實際的炮口角。炮膛軸線直線度的實測結果如表2和圖1所示，其中，x為炮膛軸線上測量點到炮口的距離，y為炮膛軸線上測量點的水平分量，z為炮膛軸線上測量點的垂直分量，w為炮膛軸線的直線度誤差；測量結果按火炮射擊方向規定，水平方向左正右負，垂直分量上正下負。

表1 某火炮炮口角的實測結果

表2 某火炮炮膛軸線直線度的實測結果

圖1 某火炮炮膛軸線直線度實測結果圖

2 仿真分析模型的基本假設

為了進行數值仿真研究，根據身管直線度的實際測量結果假設幾種身管直線度的結構形式和炮口角的偏差范圍，探究火炮身管直線度的結構形式和炮口角的偏差范圍對火炮發射時彈丸初速跳角影響的內在機理和規律，從而為炮身的設計、制造和調試制定有利于提高火炮射擊精度的技術方案。

根據實測的炮膛軸線結果，假設如下6種情況的炮膛軸線類型和炮口角偏差范圍：（a）炮口角－2.7～＋1.8mrad，含1個彎曲的身管；（b）炮口角－1.36～＋0.9 mrad，含1個彎曲的身管；（c）炮口角－1.5～＋1.5mrad，含2個彎曲的身管；（d）炮口角－1.5～＋1.5mrad，含3個彎曲的身管；（e）炮口角－1.5～＋1.5mrad，含5個彎曲的身管；（f）炮口角－1.5～＋1.5 mrad，含10個彎曲的身管。如圖2所示，圖2（a）～圖2（f）分別對應了（a）～（f）6種炮膛軸線類型。

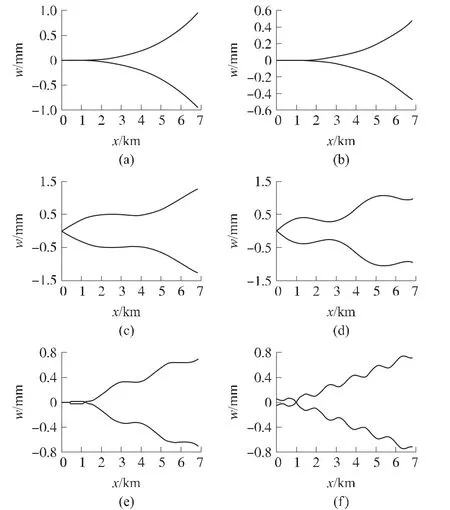
圖2 關于身管直線度誤差類型的假設

3 彈丸初速跳角散布仿真分析

對于每一個樣本身管，都要做一系列的仿真研究，每一個系列代表一個不同的初始條件，彈丸初速跳角散布是身管炮膛軸線形狀（藥溫一定范圍內隨機變化）的函數。γ1，γ2分別為彈丸初速跳角散布的橫向坐標和垂向坐標，實際發生的為γ。針對不同的炮口角θ和1彎曲、2彎曲、3彎曲、5彎曲及10彎曲身管進行計算機數值仿真分析，圖3（b）～圖3（f）是相應的仿真結果，這5種彈丸初速跳角散布的總結果見圖3（a）。由圖3可見，彈丸初速跳角分布在沿著垂向坐標的一個長條區域內，原因是在前面假設了炮膛軸線僅僅在射面內有誤差。圖3中水平坐標方向上的散布分量是火炮系統的非對稱性導致的偏差，隨著初始條件的變化而變化，從圖中可以得到一個基本結論，炮膛軸線往復彎曲的次數越多，即炮膛軸線越復雜，在炮膛內彈丸方向被強制改變次數越多，彈丸初速跳角的散布范圍就越大[4]。

圖3 不同初始條件下彈丸初速跳角散布

4 仿真結果的數據分析

比較不同炮口角情況下計算機數值仿真發射多組彈丸統計所得的彈丸初速跳角散布的系統定常偏差，分析中心線形狀的最優解。垂向彈丸初速跳角散布的系統定常偏差γA與炮口角幅值θ的對應關系，參見圖4。圖中曲線（a）～（f）為6種炮膛軸線情況，曲線（g）為身管無彎曲情況。研究過程中采用的發射藥溫度在一定的范圍內是隨機的。γA表示的是，在同一炮口角不同發射藥溫度下彈丸初速跳角散布的均值的大小。從中可知，當身管軸線彎曲的幅值減小的時候，γA也相應地減小。分析圖中的幾條曲線，得到結論：γA的分布范圍與身管軸線彎曲的幅值有較強的相關性，γA與身管軸線的彎曲個數有較強的相關性。此結論說明，彈丸初速跳角散布的定常偏差的分布與彈丸的橫向動能有關，平滑的、直線度誤差小的身管優于有多個彎曲的、直線度誤差大的身管[5]。

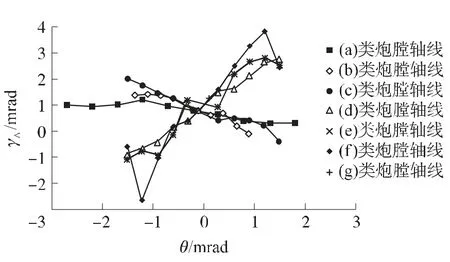
圖4 彈丸初速跳角散布的垂向系統定常偏差與炮口角幅值的關系

圖5和圖6是不同炮口角θ的單彎曲身管的仿真分析結果，圖5縱坐標是垂向彈丸初速跳角散布的系統定常偏差γA，圖6縱坐標是彈丸初速跳角散布γ。仿真包括向上彎曲和向下彎曲2種情況，只要炮膛軸線不是完全直線的，彈丸初速跳角散布的系統定常偏差就不會是0。身管分為2類：A類是身管彎曲的起點在x＝5 000 mm處（炮口角在－2.7～1.8mrad之間），B類是身管彎曲的起點在x＝3 000mm處（炮口角在－1.35～0.9 mrad之間）。圖5顯示，如果身管是一組身管，彈丸初速跳角散布的系統定常偏差的均值為0.75mrad，此結果與無彎曲身管的結果不一致，其原因是單彎曲身管的分布總是向下傾斜的。如果完全對稱，其結果將與無彎曲身管的結果一致。結果顯示，炮口角越小，身管向下彎曲的程度越嚴重，即使在炮口處炮膛軸線的曲率很小，彈丸初速跳角散布的系統定常偏差也越大[6]。這是彈丸的平動動能導致的一個結果。因此，彎曲起點于x＝3 000 mm的B類身管比彎曲起點于x＝5 000mm的A類身管，彈丸初速跳角散布的系統定常偏差的分布范圍更大。考慮到身管彎曲的個數和炮口角幅值的影響，如果身管彎曲的個數最少并且炮口角最小，則彈丸與身管之間有最小的橫向動能傳遞，具有如此形狀炮膛軸線的火炮，彈丸初速跳角散布的系統定常偏差具有最小的靈敏度。

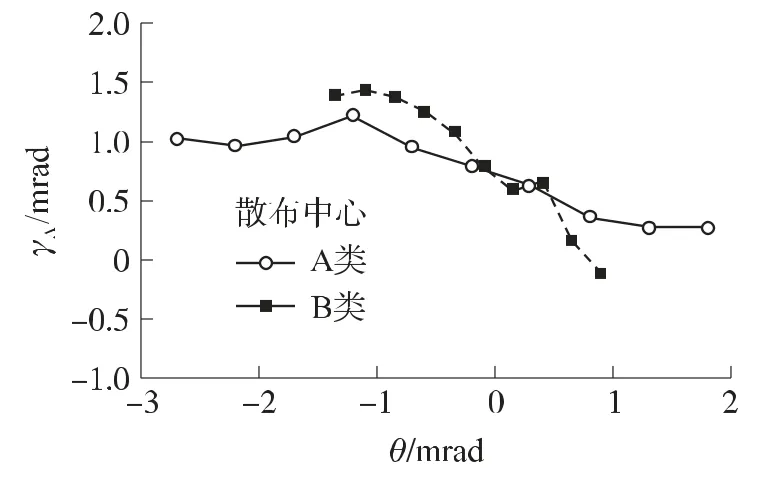
圖5 單彎曲身管彈丸初速跳角散布的垂向系統定常偏差與炮口角幅值的關系

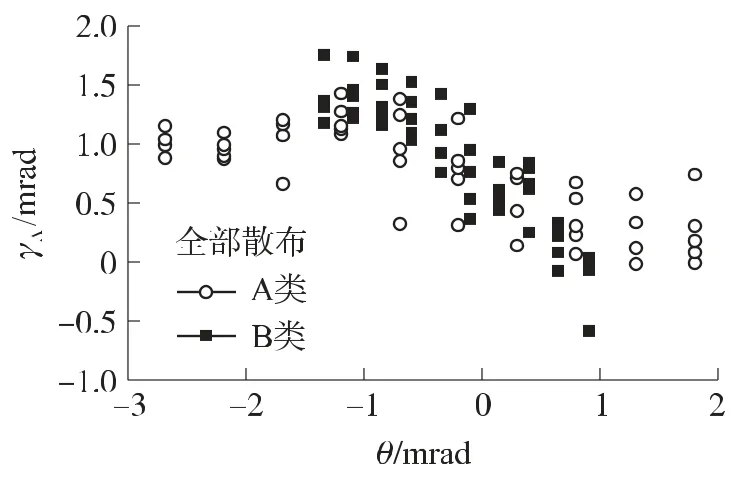
圖6 不同炮口角的單彎曲身管的垂向彈丸初速跳角散布

單彎曲身管炮膛軸線彎曲的起點不得發生于距離炮口端3 000 mm范圍內；身管炮膛軸線直線度誤差應該限制在0～＋1mm范圍內；火炮身管的炮口角限定在－1～＋1mrad范圍內。滿足上述技術要求可以將彈丸初速跳角定常偏差和散布限制在0～2mrad范圍。

5 彈丸初速跳角散布的影響

火炮最大射程地面密集度是測度火炮射擊精度的重要指標，影響火炮最大射程地面密集度的因素很多，不妨將其分為彈丸初速跳角散布和非彈丸初速跳角散布兩類，以便于研究彈丸初速跳角散布對火炮最大射程地面密集度的影響程度。設火炮縱向最大射程地面密集度的均方差為σX；σ1，σ2分別為非彈丸初速跳角散布和彈丸初速跳角散布導致的火炮縱向射程地面密集度的均方差；則σX＝，即可計算得到總的縱向最大射程地面密集度的均方差。

美軍炮兵測度火炮最大射程地面密集度的標準是50%概率偏差E，在（－4E，4E）范圍內，概率總和為0.993。概率偏差E與概率P之間的關系：

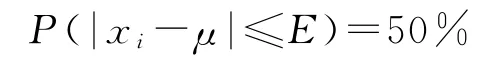
式中：xi是射程樣本值，μ是射程樣本值的數學期望[7－8]。

最大射程縱向概率偏差EX與縱向最大射程地面密集度的均方差σX的關系為：EX＝0.674 5σX。火炮縱向最大射程地面密集度一般用概率誤差表示為EX/X，X為最大射程[7－8]。

假如火炮的最大射程地面密集度EX/X為1/500，在最大射程X＝30km時，σ1＝89.95m。根據外彈道的計算，彈丸初速跳角偏差為2 mrad，最大射程的彈丸落點會有30 m的偏差，彈丸初速跳角偏差導致的落點散布也應該服從正態分布，則3σ2＝30m，σ2＝10 m。因此，σX＝90.5 m，相應的最大射程地面密集度為：EX/X＝1/491。

6 結論

身管炮膛軸線應盡量實現無彎曲或單彎曲；單彎曲身管炮膛軸線彎曲的起點距離炮口端越遠越好。炮口角在火炮裝配時置于逆重力方向偏上有利于降低彈丸初速跳角散布。現有技術條件下，彈丸初速跳角散布為2mrad，假設火炮的最大射程地面密集度為1/500，初速跳角散布導致最大射程地面密集度降低為1/491。由此可見，彈丸初速跳角散布對火炮最大射程地面密集度的影響不大。

[1]巴什卡托夫B A.火炮身管動力學數學模型及研究方法[M].圣.彼得堡：圣.彼得堡機械學院，1993.BASHKATOV B A.A mathematical model and study methods for dynamics of gun barrel[M].St Petersburg：St Petersburg Institute of Mechanical Engineering，1993.（in Chinese）

[2]郭錫福，申國太.彈丸發射動力學[M].北京：兵器工業出版社，1993.GUO Xi－fu，SHEN Guo－tai.Projectile launching dynamics[M].Beijing：Ordnance Industry Press，1993.（in Chinese）

[3]MASON B H，WALSH J L.Coupled aerodynamic and structural sensitivity analysis of a high－speed civil transport[C]// ASC Structures，Structural Dynamics，and Materials Conference and Exhibit.Seattle，WA：ASC，2001.

[4]NEWILL J F，GAMER J M，BUNDY M L.Methodology for determining optimal tank cannon barrel centerline shape[R].MD： Army Research Laboratory， Aberdeen Proving Ground，2002.

[5]BOMSTEIN J，CELMINS I，PLOSTINS P，et al.Techniques for the measurement of tank cannon jump[R].MD：Army Ballistic Research Laboratory，Aberdeen Proving Ground，1988.

[6]GUIDOS B，PLOSTINS P，WEBB D，et al.120－mm tank gun accuracy demonstrator（TGAD）jump test[R].MD：Army Research Laboratory，Aberdeen Proving Ground，1999.

[7]錢林方.彈道學[M].北京：北京理工大學出版社，2010.QIAN Lin－fang.Ballistics[M].Beijing：Beijing Institute of Technology Press，2010.（in Chinese）

[8]兵器工業系統研究所.陸軍武器系統分析[M].北京：兵器工業出版社，1997：20－35.Institute of Weapon Industry System.Army weapons system analysis[M].Beijing：Ordnance Industry Press，1997：20－35.（in Chinese）