讓圖形直觀成為學生思維的源泉
摘 要:直觀是一種重要的教學手段。在小學數學教學中,合理利用圖形直觀,既充分體現出了數形結合的數學思想,也體現出數學學科的重要性質。利用圖形直觀,給學生一個思維的支點,能幫助學生的思維切入基本點、捕捉生長點、構造交接點、把握中心點。
關鍵詞:圖形直觀;基本點;生長點;交接點;中心點
直觀是一種重要的教學手段。在實際的小學數學教學中,合理利用圖形直觀,可以幫助學生找到思維的支點,能夠更好地促進學生理解、掌握、建構知識,發展學生的思維。那么,在實際的教學中如何利用圖形直觀,讓它成為一個有效的載體,真正成為學生思維的源泉呢?下面結合自己的教學實例,談談自己的一些做法和體會。
一、圖形直觀,切入基本點
利用圖形直觀,抓住概念的本質,以知識本身為基本點,可以幫助學生修正自己的猜測,感悟“做數學”,提升思維品質。如,教學四年級下冊的“三角形三邊關系”,有許多的教學案例出現,學生認為兩邊之和等于第三邊的情況是能夠做成三角形的。我通過觀察、分析,發現問題就出在缺乏概念支撐上。當學生用小棒做三角形時,課堂上我就讓學生反饋一下,做的三角形在哪里,讓學生指一指邊、角、頂點。用的材料是“圍”成三角形,而不是拼搭,必須有三個角、三個頂點、三條邊,缺其中之一都無法圍成三角形。圖形直觀,概念抽象化出邊、角,實現對三角形三邊關系的真正意義的理解,讓學生的判斷力有所依靠,在否定自己的認識和推理過程中來建立、優化對數學知識的正確認識。利用圖形直觀,幫助學生切入到思維的基本點,培養學生探究意識的同時發展思維的正確性和深刻性。
二、圖形直觀,捕捉生長點
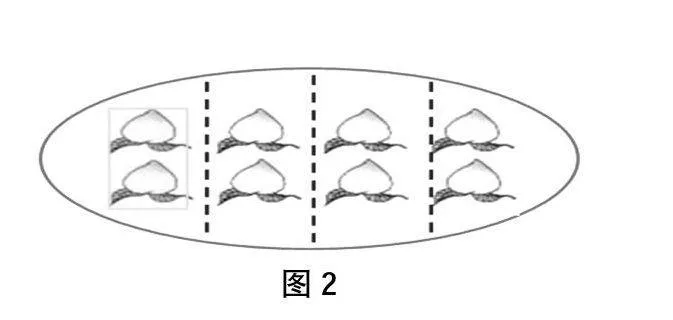
利用圖形直觀,發揮其符號意義的功能,以舊知識為生長點,能更好地促進學生對新知識的接納和理解,實現“同化”與“順應”。如,教學三年級下冊“分數,認識幾分之一”時,學生對把由許多個物體組成的整體來平均分,總會受個數的影響,難以理解把一個整體平均分成幾份,每份是這個整體的幾分之一。我看過的課例中都重新創新教材,回避把4個物體(桃)平均分的情況,直接出現8個物體平均分,仍會出現平均分成4份,每份是整體的八分之二。應對課堂,回避總不是問題。再回到4個桃平均分,如圖1,學生很容易理解每份是1個,這1個是這個整體(4個桃)的四分之一,分母4表示的是平均分成4份,分子1表示的是1個1份,這1份是這個整體(4個桃)的四分之一。那8個桃平均分成4份,每份是這個整體的四分之一還是八分之二呢?關鍵還在于理解分數的意義。當學生出現理解為八分之二時,就反問學生從8等份中取2份,怎樣畫圖?像圖2的分法中還缺少什么?學生容易想到還要把這個整體(8個桃)平均分,要分成8份,還要畫一條虛線,再取2份。利用圖形直觀,通過圖式對比,變化虛線符號,讓學生思維的由靜態發展到動態,直觀中精細化,幫助學生捕捉到思維的生長點,實現了新舊知識之間的遷移。
三、圖形直觀,構造交接點
利用圖形直觀,突出其新舊知識的聯系,交織融會為交接點,能夠更好地促進學生對數學學習的系統認識,思維方式、方法得以提升。如教學四年級下冊“倍數和因數的知識”,教材呈現出對12個小正方形拼成的長方形(教材70頁圖):其意義是從三種拼法中來揭示“倍數和因數”的知識。究竟基于的起點和路徑是什么呢?我想還是反饋課堂來尋求吧。課堂上學生反饋出的拼法中就有把每一種情況都豎起來的得到的是六種拼法,及是學生一圖兩用了。我沒有否定學生的想法,而是告訴學生拼成的長4,寬3的長方形,既可以看成12里面有3個4,也可以看成12里面有4個3。正是因為學生會一圖兩用,順理成章就可以揭示出倍數的概念,更好地理解為什么12是4的倍數,也是3的倍數了。當然學生再理解研究倍數和因數時為什么不研究0呢,而是研究0以外的自然數才有意義,這也就成順其自然的事了。利用圖形直觀,搭建起新舊知識的聯系,為學生構造出思維的交接點,獲取到新知識信息的途徑,讓學生的思維得到順應,強化所學知識的系統性。
四、圖形直觀,把握中心點
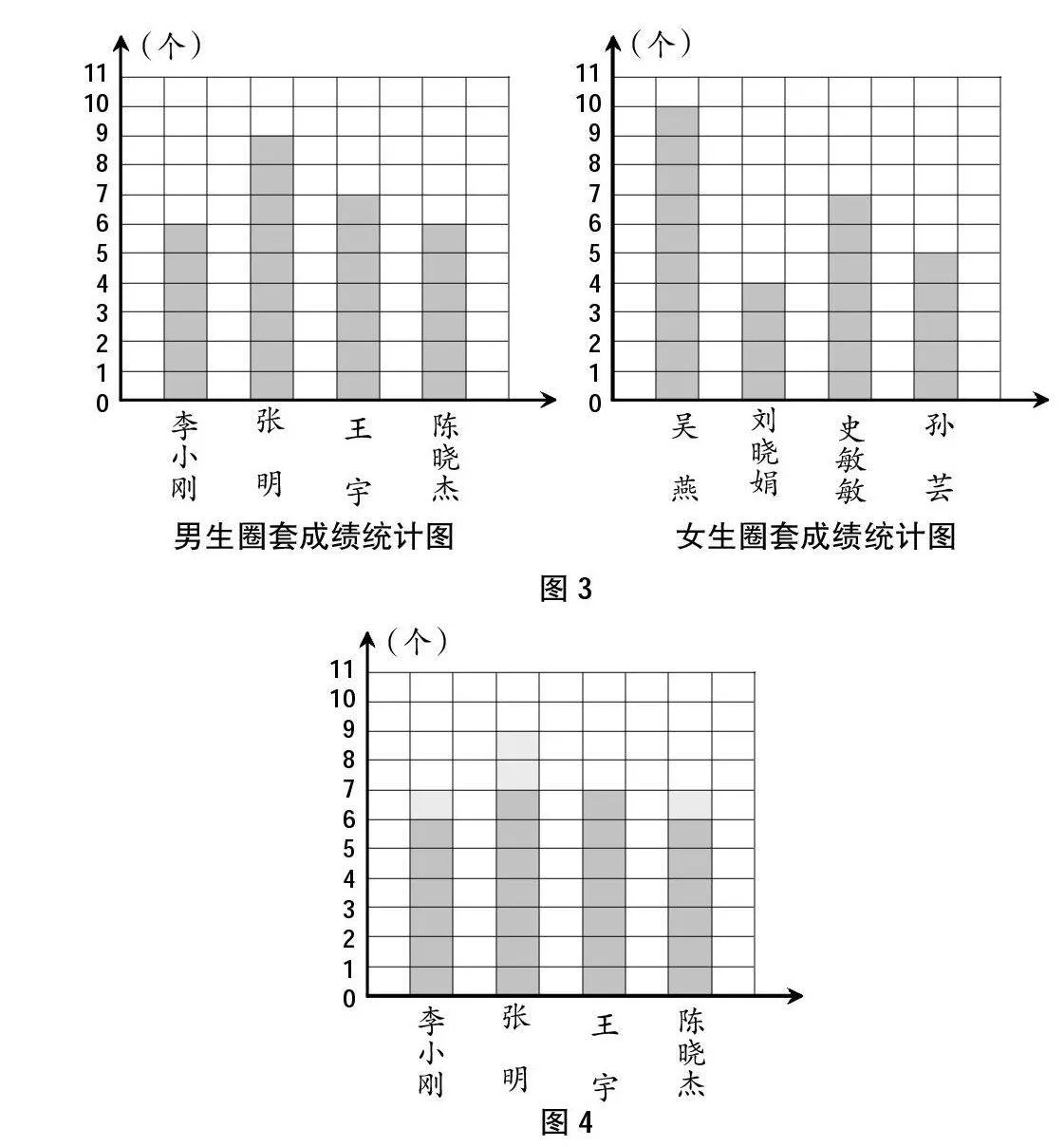
利用圖形直觀,強化數學知識學習的理解,以數學思維方法為中心點,培養了學生解決問題的意識。如教學三年級下冊統計單元的“平均數”,處理這一部分內容時應該是一個整體性的把握,教學中應該把理解平均數的意義和求平均數的方法聯系在一起,有效地整合。結合教材呈現的條形統計圖,如圖3,課堂上組織學生討論男生和女生,哪一組套得準一些,究竟選取哪個數據來比較呢?學生會發現比總數、個別數據都不行,而要比整體的一般水平,即需要找到能夠表示這一組數據集中趨勢的一個統計量,這個統計量就是平均數。怎樣求平均數呢?學生就可以借助圖形直觀,發現“移多補少”,這個就是求平均數的基本方法。課堂上教師及時追問學生從計算的角度來研究,怎樣算呢?學生會聯系學過的平均分的知識,先求和再平均分,進而得到求平均數的一般方法。再進一步追問學生平均數會不會超過最大的9個呢?如圖4,為什么?學生會從移多補少的過程中,解釋把最多的要移掉是減少,所以平均數不會比最大的9個大。同樣,會比最小的6個少嗎?為什么?學生會解釋最少的是從多的那里得到的,不會比自己更少的了。變與不變,學生能夠自主獲得解釋和理解平均數是介于最大值、最小值之間,主動形成“區間套”的數學思想。利用圖形直觀,知識承載思想與方法,幫助學生把握住了思維的中心點,使得學生能夠“知其然,又知其所以然”,培養了學生解決問題的意識。
綜上所述,圖形直觀是數形結合思想的重要體現,也是數學學科性質的重要體現。在實際的小學數學教學中,利用圖形直觀,給予學生一個思維的支點,能夠幫助學生理解、掌握、建構知識,發展數學思考,促進學生的思維發展。給予兒童思維的源泉,這是蘇霍姆林斯基提倡的發展兒童智力的建議。那么,在我們的數學課堂中,圖形直觀就是學生思維的重要源泉。
參考文獻:
[1]中華人民共和國人民教育編輯部.教學大道:寫給小學數學教師[M].北京:高等教育出版社,2010(04).
[2]鄭毓信.數學思維與小學數學[M].南京:江蘇教育出版社,2008(08).
[3][蘇]B.A.蘇霍姆林斯基.給教師的一百條建議.杜殿坤,譯.北京:教育科學出版社,2010(02).
(作者單位 江蘇省張家港市合興小學)

