求解0－1背包問題的動態規劃改進算法分析

李軍民，傅云鳳

(西安科技大學計算機學院，陜西西安 710054)

0-1背包問題［1］是一個典型的NP難問題，可作為許多工業場合的應用模型，如資本預算、貨物裝載和存儲分配問題等。對該問題的求解，既具有理論價值又具有實際意義。目前已有的求解方法可分為兩大類，一類是精確算法，如動態規劃算法［2］、回溯法［3］、分支限界法［4］;另一類是近似算法，如貪婪法［5］、蟻群算法［6］和遺傳算法［7］。本文對文獻［8］中的動態規劃改進算法進行分析，此算法存在不足之處:其空間資源浪費較大。為了克服這一缺點，本文提出了采用動態鏈表存儲數據的實現方式改進此算法，從而達到改善其空間復雜度的目的。

1 問題描述

給定n種物品和一個背包，對n種物品進行編號 1，2，…，n，物品 i的重量 wi，其價值 pi，背包容量為 c，給定c ＞ 0，wi＞ 0，pi＞ 0，1≤i≤n，要求找出一個 n 元向量(x1，x2，…，xn)，xi∈ {0，1}，使得達到最大。

2 求解0－1背包問題的動態規劃算法

2.1 0－1背包問題的最優子結構性質

根據0－1背包問題的描述，其具有最優子結構和重疊子問題性質。最優子結構即:設(x1，x2，…，xn)是0－1背包問題的最優解，則(x2，x3，…，xn)是子問題(從物品2至物品n中選取，裝入背包)的最優解。

2.2 規劃數學模型

設m(i，j)是背包容量為j時，可選物品是i，i+1，…，n時0－1背包問題的最優值。則可建立遞歸關系式

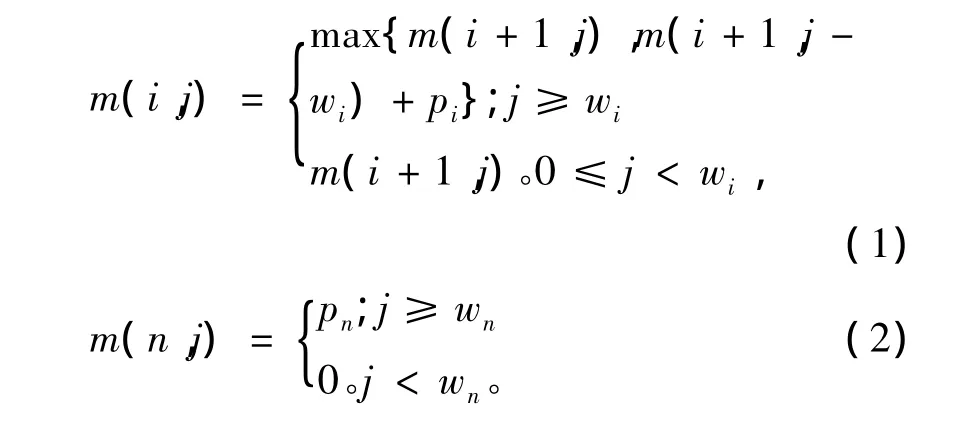
3 一種動態規劃法的改進算法分析

3.1 該動態規劃改進算法的思路

由m(i，j)的遞歸式可知，在一般情況下，對每一個確定的i，函數m(i，j)是關于變量j的階梯狀單調不減函數［8］。跳躍點［9］是這一類函數的描述特征。在一般情況下，函數m(i，j)由全部跳躍點唯一確定，因此，針對每一個i值，只記錄m(i，j)的跳躍點(j，m(i，j))也可求出背包問題的最優解和最優值。

該算法對于每一個確定的i采用表c［i］來記錄函數m(i，j)的全部跳躍點。c［i］可依據式(1)和式(2)遞歸的由c［i+1］得到，初始時令c［n+1］={(0，0)}。函數m(i，j)的全部跳躍點是函數m(i+1，j)的跳躍點集c［i+1］和函數m(i+1，j－ wi)+pi的跳躍點集d［i+1］的并集，d［i+1］由c［i+1］來確定，公式如下

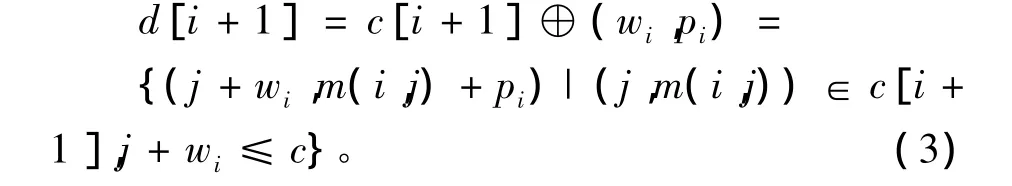
設(a，b)和(c，d)是 c［i+1］∪ d［i+1］中的兩個跳躍點，當c≥a且d＜b時，(c，d)受控于(a，b)，將(c，d)刪除。因此，在由 c［i+1］計算c［i］的過程中，先由 c［i+1］計算 d［i+1］，再合并 c［i+1］和 d［i+1］，并清除受控點得到 c［i］。

3.2 該動態規劃改進算法的分析

此算法采用二維數組c［］［2］記錄跳躍點的坐標值(j，m(i，j))，從而實現表 c［i］對跳躍點的記錄。此算法的空間復雜度在于跳躍點集(j，m(i，j))(1≤i≤n，0≤j≤c)存儲所占用的空間，因此其空間復雜度為

此算法對于每一次求得的跳躍點集c［i］(1≤i≤n)都記錄于二維數組c［］［2］中，跳躍點集c［i+1］和c［i］存在相同的跳躍點，這些相同的跳躍點需要重復記錄于數組中，且使用靜態數組，事先需要定義較大的數組來避免溢出的發生，這樣使得空間資源浪費較大。

4 利用動態鏈表記錄跳躍點改進上述算法

為了克服上述算法求解0－1背包問題的不足，本文采用動態鏈表結構存儲跳躍點集，來減輕空間資源的浪費，其算法介紹如下。

4.1 改進算法的思路

1)對每一個確定的i，仍用一個表c［i］來存儲函數m(i，j)的全部跳躍點(j，m(i，j))(0 ≤j≤c)，但采用動態鏈表結構實現表c［i］對跳躍點集的記錄。

2)由式(1)和式(3)可知，跳躍點集c［i］可由表 c［i+1］和表 d［i+1］確定，表 d［i+1］可由c［i+1］確定。初始時，令c［n+1］={(0，0)}，新建一個鏈表結點，其重量和價值均為0，以此來實現對跳躍點(0，0)的記錄。

3)由式(3)求跳躍點集d［i+1］時，設置一個布爾型變量，標識表d［i+1］中每次求得的點是否受控。將上述判斷受控點的標準改為:設??(a，b)∈c［i+1］，??(c，d)∈d［i+1］，當a ＞ c，b≤ d 或 a=c，b ＜ d 時，(a，b)受控于(c，d);當 c≥ a，d ≤ b時，(c，d)受控于(a，b)。每次求得表d［i+1］中的一個點時，判斷其是否為受控點，若不為受控點，將其加入鏈表;否則，舍棄;同時查看表c［i+1］中的點是否受控，若受控，則標記其為新增受控點。

4)在求得跳躍點集d［i+1］后，遍歷整個鏈表，若鏈表中的結點被標記為新增受控點，則標記該結點已受控。遍歷鏈表結束時，沒有標記為已受控的跳躍點集就是 c［i］。這樣就由表 c［i+1］和表 d［i+1］求得表 c［i］。

5)按照上述方法，可遞歸地求出表c［1］，它記錄了m(1，j)的全部跳躍點。由于鏈表中記錄的跳躍點不是按照m(i，j)值由小到大的順序排列的，需要遍歷鏈表尋求價值最大的結點，該結點的價值即為最優值。

6)構造最優解，其步驟為:

Step1 初始時，令i=1，y初始化為式(5)中求得的價值最大的結點的重量值j0，m初始化為該結點的價值m(1，j0)。

Step 2 遍歷鏈表中的所有結點(j，m(i，j))(1 ≤ i≤ n，0 ≤ j≤ c)，如果 ?(j'，m(i'，j'))使 j'+wi=y，m(i'，j')+pi=m 成立，則 xi=1，y=j'，m=m(i'，j');否則 xi=0;然后令 i++。

Step 3 重復Step2，直至i＞n為止。

4.2 改進算法的分析

此改進算法采用動態鏈表記錄跳躍點集，其空間復雜度在于跳躍點集的存儲。但是，不需要重復記錄已存在的跳躍點，只需將每次求得的新增跳躍點加入，又每次求得的跳躍點個數不超過2i，故最終求得的跳躍點總數不超過2n。因此，空間復雜度為O(2n)。

該方法遞歸地求出跳躍點集c［1］，不需要重復記錄已存在的跳躍點。所以不存在同一跳躍點的重復記錄問題，且采用動態鏈表結構記錄跳躍點，大大節省了空間資源，彌補了采用二維數組記錄跳躍點這種動態規劃改進算法的不足。

5 算法測試實例

有5種物品和一個背包，背包容量為100，裝入的物品不可分割，求取此0－1背包問題的最優解和最優值。每種物品的重量和價值如表1所示。

動態規劃法、二維數組記錄跳躍點的動態規劃改進算法和動態鏈表記錄跳躍點的動態規劃改進算法，采用i記錄物品編號，利用數組w［n］記錄物品重量，數組p［n］記錄物品價值，bestp記錄最優值，x［n］記錄最優解。3種方法解決本例中的0－1背包問題的運行結果對比如表2所示。程序運行時間以秒為單位，n值較小時，3種方法的程序運行時間幾乎沒有差異;當n值取100時，動態鏈表記錄跳躍點的動態規劃改進法的運行時間較前兩種方法在十分位出現差異。

表1 背包問題信息表Tab．1 Information sheet of knapsack problem

表2 3種方法解決0－1背包問題的運行結果比較Tab．2 Comparison of computational results of three methods solving 0 －1 knapsack problem

表2表明，采用上述3種方法，該0－1背包問題的最優解、最優值和裝入背包的重量均相同，進而表明動態鏈表結構記錄跳躍點集的動態規劃改進算法的有效性。通過空間復雜度的對比，驗證了動態鏈表結構記錄跳躍點集的實現方式在降低空間復雜度方面的優越性。

動態規劃法的空間復雜度在于記錄函數m(i，j)的值，空間復雜度為 Ω(nc)。二維數組存儲跳躍點的動態規劃改進法的空間復雜度為，動態鏈表記錄跳躍點的動態規劃改進法的空間復雜度為O(2n)。前兩種方法均采用二維數組存儲數據，為了避免溢出情況的發生，需要預先定義較大的存儲空間。隨著n值的增大，且在c值較大的情況下，動態鏈表結構記錄跳躍點集的實現方式在降低空間復雜度方面的優越性越明顯。

6 結語

本文基于動態規劃法的一種改進策略，進行算法分析，進而提出其改進算法，改善了原算法的空間復雜度。通過實例驗證了該改進算法的有效性，且證實其空間復雜度的優越性。隨著n值的增大，且在c較大的情況下，此改進算法的空間復雜度優越性越明顯;但是，它的程序運行時間較前兩種方法要長一些。為了使該改進算法的應用價值更好地發揮出來，今后，將嘗試利用該改進算法的思想解決其他問題。

［1］ 王曉東.計算機算法設計與分析［M］.北京:電子工業出版社，2012，2.

［2］ 唐敏，劉冠蓉.用動態規劃法和貪心法解決背包問題［J］.軟件導刊，2007(5):111-113.

［3］ 劉繼，夏定純.用動態規劃法與回溯法實現0-1背包問題的比較［J］.科技信息，2010(19):458.

［4］ 趙鑫.0/1背包問題分支限界法在C++程序實現中的難點解析［J］.產業與科技論壇，2012(3):69-70.

［5］ 蔣力，武坤.0-1背包問題貪婪算法應用研究［J］.計算機與數學工程，2007(6):32-33.

［6］ 秦玲，白云.解0-1背包問題的蟻群算法［J］.計算機工程，2006(6):212-214.

［7］ 王莉，紹定宏.基于遺傳算法的0/1背包問題求解［J］.計算機仿真，2006(3):154-156.

［8］ 呂聰穎，趙剛彬.求解0-1背包問題的動態規劃分析［J］.南陽理工學院學報，2011(2):17-21.

［9］ LEVITIN A.算法設計與分析基礎［M］.北京:清華大學出版社，2004.