低頻超寬帶步進頻率收發系統的設計與實現

張漢華，梁福來，宋 千

(國防科學技術大學電子科技與工程學院， 長沙410073)

0 引言

地表穿透雷達(Ground Penetrating Radar，GPR)利用電磁波在地表媒質電磁特性不連續處的反射和散射，實現對淺表層的成像、定位，進而定性或定量地辨識地表中的電磁特性變化，實現對表層下目標的探測。20世紀60、70年代，等效采樣技術和亞納秒脈沖產生技術的發展，從技術角度加速了GPR的發展。隨后，該技術在市政工程、考古、地質、探雷等方面廣泛地應用起來［1-5］。早期的GPR系統一般采用沖激脈沖體制，然而，隨著探測要求的提高，沖激體制GPR碰到越來越多的瓶頸，如:帶寬和時寬的矛盾、超高的瞬時帶寬對電子器件的要求等等。隨著微波技術、數字信號處理技術、大規模集成電路技術以及頻率綜合器件水平的發展，步進頻率體制憑借著獨特的優點開始嶄露頭角，并迅速出現在雷達的各種應用領域［6］。目前，多款基于步進頻率體制的超寬帶GPR系統已研制完成并投入使用［7-12］，如:南非開普敦大學的Mercury-A和Mercury-B雷達，美國PSI公司的FLGPR系統和SRI研究所的FLGPSAR系統等。國防科學技術大學將超寬帶SAR技術引入GPR領域，在理論研究和系統研制上取得了一系列進展［13-16］。由于GPR需要工作在低頻段，絕對帶寬要求比較大，射頻干擾較為嚴重，因此，收發系統的設計與實現成為低頻超寬帶步進頻率GPR系統開發的關鍵技術之一。本文面向低空探地應用，著重討論了超寬帶脈沖步進頻率雷達收發系統的參數設計、信號源的設計實現以及收發系統射頻凹口的設置和修復，最后用一維距離像的拼接結果驗證了低空無人機載收發系統的整體性能。

1 低頻超寬帶步進頻率收發系統的參數設計

在低空探地應用中，脈沖步進頻率體制是一個不錯的選擇［17-18］:一方面，步進頻率體制能夠利用較小的瞬時帶寬合成較大的有效帶寬，不僅可方便靈活地對信號各離散頻點的頻率值和幅度值進行精確調整，具有良好的數字可控性，還極大地降低了對接收機和A/D采樣的帶寬要求，從而能夠有效地抑制噪聲和干擾，提高接收機的靈敏度。另一方面，脈沖信號可工作于單天線模式，有利于減輕雷達系統的重量，并且由于窄脈沖本身的距離解算能力，可以在某些特定的系統參數設定下解距離模糊，從而能夠適應更遠的作用距離，有利于提高低空平臺的作業高度及偵察范圍。

1.1 頻段選擇

目標及環境的反射特性是雷達頻率范圍選擇的主要依據。由于要探測淺層地下目標，雷達波必須能夠穿透地表土壤，因此，土壤對雷達波的衰減是頻段選擇的重要因素。一般地，土壤介電常數和導電率是與土壤類型、土壤含水量、電磁波頻率等其他參數有關的變量，電磁波在土壤中的實際穿透損耗難以通過建立一個以簡單易測的參數為變量的確知模型來表示。因此，土壤的電磁特性一般為大量實驗的測量結果。表1為美軍針對多種類型土壤測量數據在6個典型頻點上穿透損耗的統計結果［19］。

表1 美軍關于土壤穿透性能測量數據的統計結果

從表1可以看出，土壤穿透損耗隨著電磁波頻率的增加而大幅增加，故而高頻段的電磁波不適用于探測土壤中的目標。而頻率太低，對于無人機載平臺來說，不利于系統整體的低功耗、輕型小型化設計。而且由于土壤介電常數的實部大于1［20］，考慮到土壤對雷達信號的選擇性，目標發射波的實際有效帶寬要小于雷達的發射帶寬，為了達到0.1 m的距離分辨率，低頻超寬帶步進頻率收發系統的頻段選擇為0.5 GHz～2.5 GHz。

1.2 收發系統的參數匹配

步進頻率收發系統的參數匹配問題在雷達總體設計階段非常重要，其關鍵參數包括:脈沖重復周期Tr，發射脈沖寬度τ，頻率步進增量Δf，頻率步進數N，采樣速率 fs等［21］。

實際測量顯示，信號有效頻段內平臺工作環境中的射頻干擾噪聲基底電平在-60 dBmW以下，假設干擾在成像過程中不會相干積累，為便于對目標進行有效檢測，期望成像后目標信雜比大于10 dB。在此條件限制下，結合平臺功耗的限制，根據雷達方程，可推出有效探測距離≤300 m，故而選擇脈沖重復周期Tr=2 μs。

由于步進頻率雷達頻域采樣，其時域距離像必然存在周期性，即存在距離模糊，理論上只要τ·Δf＜1，就可利用發射脈沖信號自身具有的解距離模糊能力解除時域距離像的模糊［22-24］。在雷達總帶寬和脈沖重復周期確定的情況下，Δf越大，掃描時長越短，越有利于雷達探測的實時性。從折中角度以及保留一定的信號處理裕度，取 Δf=2 MHz，τ=250 μs，對應距離盲區37.5 m。

理論上一個脈沖寬度內能采到一個采樣點就可以拼接出完整的時域無模糊距離像。考慮到實際中為了盡可能減小I/Q通道不平衡的影響，步進頻率雷達接收機通常采用數字中頻正交解調，即先采集下變頻后的中頻信號，再在數字域實現中頻正交解調，故而在中頻正交解調前先深度過采樣，中頻正交解調后再對數據進行抽取降采樣率，最后等效為fs=4 MHz。

2 低頻超寬帶步進頻率源的設計與實現

目前常用的頻率相參合成技術主要有直接數字頻率合成(Direct Digital Frequency Synthesis，DDS)技術和鎖相環頻率合成(Phase Lock Loop Frequency Synthesis，PLL)技術。單純利用DDS技術合成信號，存在輸出帶寬窄、諧波電平高、雜散抑制性能較差的不足，而擴展的DDS技術合成高頻譜質量的寬帶步進頻率信號的實現難度較大［25］。相比DDS的開環電路，PLL的閉環自動相位調節在頻率和相位特性上具有輸出頻帶寬、雜散抑制好、頻率自動鎖定等優勢;但其主要缺點是相位鎖定需要較長的時間，因此，其頻率切換時間較長。為了滿足頻率(ns級)快速步進的要求，考慮多個鎖相環并行分時工作。

2.1 并行分時工作結構

鎖相環的鎖定時間可以分為鎖頻時間和鎖相時間［26］。設第k鎖相環鎖頻時間和鎖相時間之和為Tk，那么可以采用圖1中的結構，將多個鎖相環并行分時工作，以提高整個頻率源的頻率切換時間。

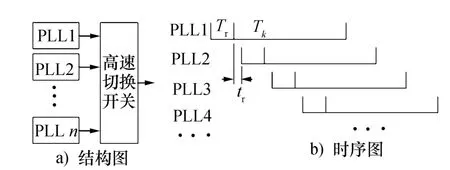
圖1 鎖相環并行分時工作示意圖

圖1中，Tr為每個頻率點的工作時間，即脈沖重復時間，tr為高速開關并行工作的多個鎖相環之間的切換時間。為了將頻率源頻率切換時間從鎖相環的μs級鎖定時間縮短到高速開關ns級切換時間，并行分時工作的鎖相環最少需要N個

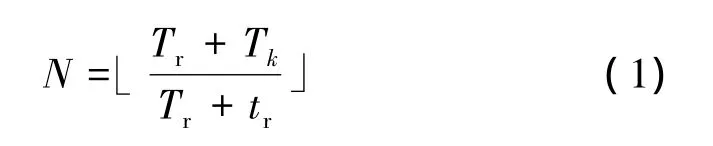
式中:[·]為向上取整。

圖1這種并行分時結構除了將頻率源頻率切換時間縮短到了ns級外，還有如下優點:

(1)可靠性高:頻率合成器互相獨立，某一個頻率合成器出現故障，不影響其他頻段，頻率源和雷達仍然可以繼續工作;

(2)靈活性好:不同頻段的頻率合成器PCB電路設計是一致的，可以進行模塊化設計;

(3)可擴展性高:利用式(1)增減頻率合成器的個數即可滿足不同步進頻率脈沖雷達μs脈沖重復時間的要求。

2.2 超寬帶步進頻率源的實現

整個收發系統在設計中只使用一個步進頻率源，如果使用分數倍頻，可使用相對較高頻率的晶振(例如100 MHz恒溫晶振)作為系統基準源和鎖相環的參考頻率源，并以此為基礎提高鑒相頻率，以縮短鎖相環的鎖定時間。Analog Device公司生產的低相噪快鎖芯片ADF4154正是采用分數倍頻和自動切換功能的頻率綜合器，其2 M鎖定時間小于13 μs。為保證鎖定的可靠性，可使用8個頻率合成器不間斷循環頻率切換，實現脈沖跳序步進頻率雷達(見圖2)，進行后端的數字處理時再將其還原成脈沖順序步進頻。

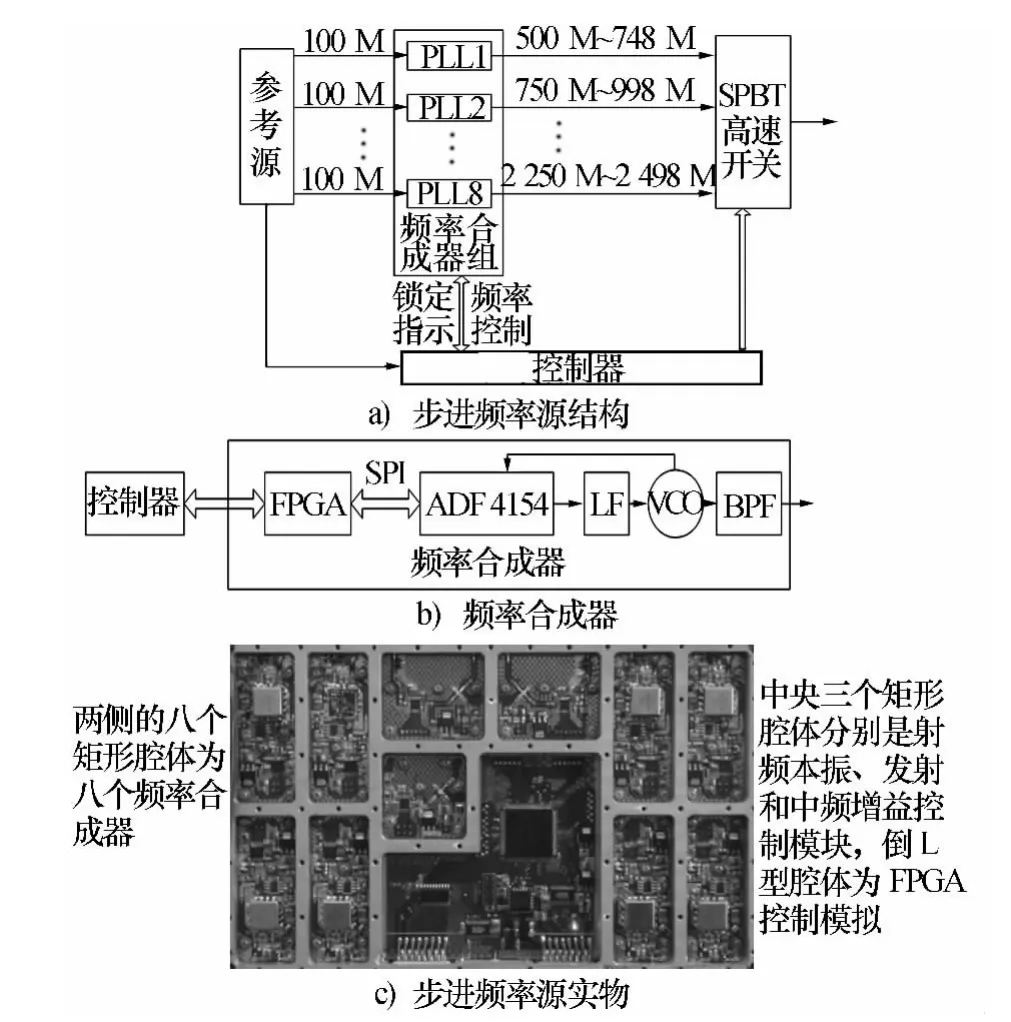
圖2 收發系統中步進頻率源部分

2.3 步進頻率源測試

表2為射頻本振信號的頻譜測試結果，表3為發射信號的頻譜測試結果。圖3為中頻本振信號的頻譜測試結果。由測試可知，本振三個頻點雜散都控制在-80 dBc以下，相噪都控制在-85 dB/Hz@10 kHz以下。發射信號的雜散(SFDR)和相噪特性與射頻本振信號類似，由于中頻信號的引入，正交調制電路以及功分和差分轉換電路的影響，對應頻點的發射信號比射頻本振信號有所惡化。在衰減量100 dB，即回波信號功率為-100 dBm的情況下，中頻信號相噪仍然達到了-60 dBc/Hz@1kHz。由此說明，接收機動態范圍大于80 dB。

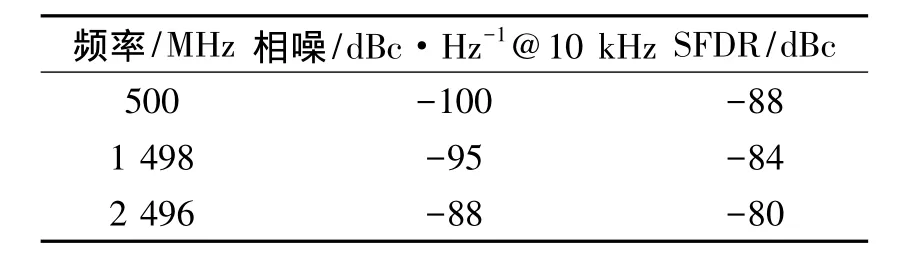
表2 射頻本振信號的相噪和雜散

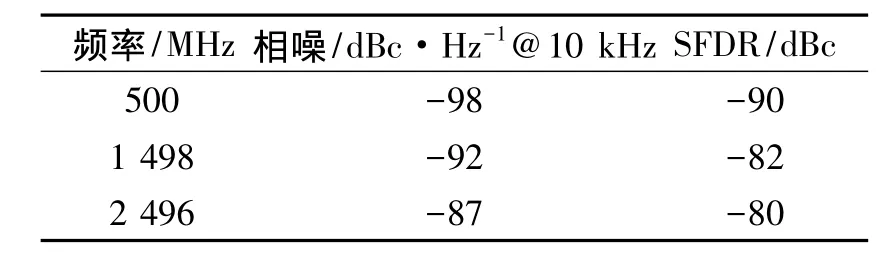
表3 發射信號的相噪和雜散

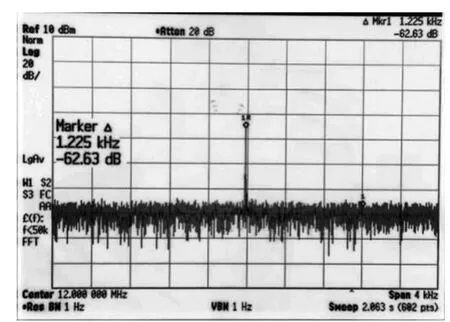
圖3 中頻本振信號頻譜(回波信號功率為-100 dBm)

3 收發系統射頻凹口的設置和修復

3.1 射頻凹口的設置

對于傳統超寬帶SAR來說，1 GHz以下存在著電視、廣播、移動通信等大量射頻信號，干擾非常嚴重，需要設計性能優良的濾波器抑制射頻干擾(Radio Frequency Interference，RFI)。常見的RFI可分為兩類:第一類RFI在時間和頻率上是穩定、確知的，主要包括無線電管理委員會嚴格限定的廣播和電視信號，以及無人機平臺無線鏈路通信、遙測遙控通信等信號;第二類RFI為時域上不連續或頻率上變化的信號，例如GSM手機發射信號在875 MHz～925 MHz頻段范圍內的隨機分布，峰值帶寬隨機出現。對于第二類RFI，通常在信息處理算法中采用自適應估計的方法來抑制;對于第一類RFI，由于步進頻率雷達每個脈沖發射的均為單頻信號，所受的干擾影響相對來說要弱一些，可通過設置頻率凹口的方法抑制少量較高的窄帶干擾，如圖4所示。

射頻凹口的設置，一方面可避免其幅度過強影響接收機動態范圍，另一方面可避免強RFI震蕩旁瓣污染拼接出的時域距離像。其缺點是將使二維SAR圖像的點擴展函數PSF出現不期望的旁瓣，這將對淺層地下弱目標的檢測產生不利影響。需要根據頻譜上數據之間的相關性，利用數據內插和外推技術對這些射頻凹口進行信息修復［27-29］。

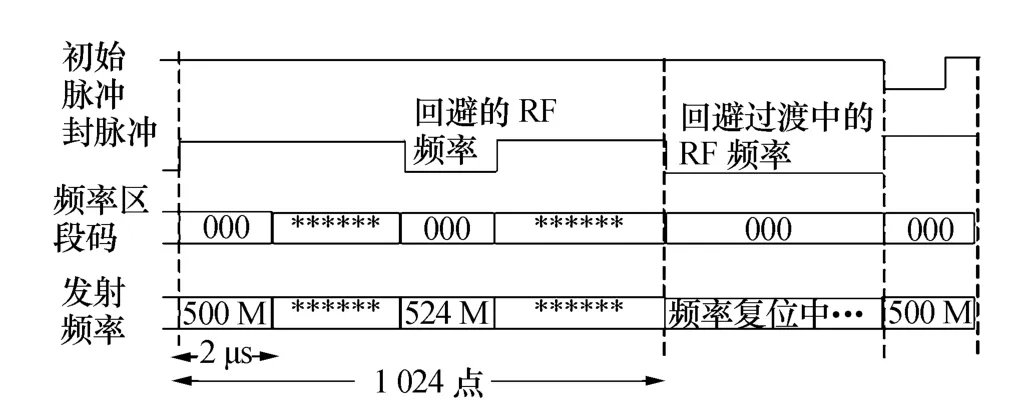
圖4 子頻率脈沖控制時序圖

3.2 基于CG模型的凹口修復算法

當噪聲服從高斯分布時，回波頻譜數據符合柯西分布，可建立CG(柯西-高斯)模型對線性譜數據進行內推和外插估計［31］。借助貝葉斯理論并利用數據本身性質，產生一個目標函數作為迭代的限制條件。這個目標函數的超越參數控制估計數據匹配程度和譜分辨率，還可達到消除噪聲的目的。

凹口處頻譜信息修復可理解為已知N個序列x0，x1，…，xN-1，估計 M 個序列 X0，X1，…，XM-1，且 M＞N。該過程等價為解線性系統方程

式中:x∈RN為已知信息;X∈CM為未知信息;F為N×M維矩陣。

稀疏的譜幅度分布可提供一種使式(2)正則化的方法。假設X的先驗分布符合柯西分布

式中:t為判決門限。當迭代停止條件滿足時，就計算出了^X，這樣就實現了射頻凹口修復。一般來說，只需少數(μ＜10)迭代就可完成。

3.3 基于CG模型的凹口修復效果分析

基于CG模型的凹口修復算法可用數字信號處理器(Digital Signal Processor，DSP)完成。該算法的一個重點是參數gx的估計以及代價函數門限值t的選取。選取σn=0.3，信噪比SNR為20 dB，凹口位置如圖5所示，每個凹口寬度為5 MHz。設恢復數據與原始數據之間方差為

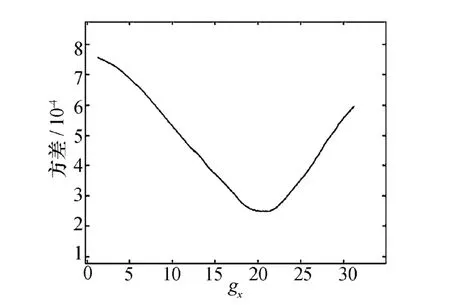
圖6 gx與方差Δ的關系圖

從圖6可見，gx≈20時方差最小，即此時數據恢復效果最好。圖7為仿真數據的修復結果。

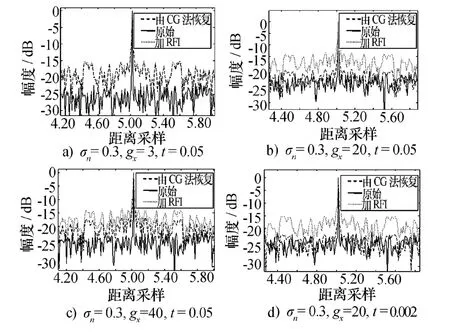
圖7 凹口修復仿真

圖7驗證了圖6的分析結果，并且從圖7可見，減小門限值可提高恢復效果，但提高程度很小。這是因為當門限值達到一定數量級時，迭代的貢獻越來越小，反而使運算量增大，因此一般選擇t=0.05。

3.4 收發系統閉環測試結果

由于低頻超寬帶天線色散很大，故只在實驗室環境下，對收發系統進行閉環測試。射頻本振信號功率10 dBm，發射信號衰減到-20 dBm，延長線長度分別為3 m，8 m，對應目標距離分別為1.5 m，4 m。測試結果為數字中頻解調、凹口修復、拼接后的一維距離像(見圖8，圖中所示的點坐標為最大旁瓣頂點坐標)。

圖8 閉環一維距離像測試結果

圖8b)中8 m延長線一維脈壓得到的峰值旁瓣比圖8a)中3 m延長線差，是由延長線功率損耗引起的。從測試結果可以看出，本文設計的收發系統性能良好，接后的一維距離像雜散＜50 dB，底噪＜61 dB，峰值旁瓣比＜-39 dBc。

4 結束語

對于地下目標和地表隱藏目標來說，低空探測是全方位立體探測層面中不可或缺的一個環節。面向低空探地，本文重點介紹了超寬帶步進頻率脈沖雷達收發系統設計和實現中的幾個關鍵技術。文中設計、實現的大帶寬和快速步進能力的步進頻率信號收發系統，體積小、重量輕、性能良好，適合低空無人機載平臺使用，為后續高分辨大范圍的SAR成像及淺層地下目標的探測等信號處理研究，打下了良好的基礎。

［1］ Burrell G A，Peters L J.Pulse propagation in lossy media using the low-frequency window for video pulse radar application［J］.Proceedings of the IEEE，1979，67(7):981-990.

［2］ Riek L，Crane R K，Neill K O.A signal-processing algorithm for the extraction of thin freshwaterice thickness from short pulse radar data［J］.IEEE Transactions on Geoscience and Remote Sensing，1990，28(1):137-145.

［3］ Gurel L，Oguz U.Simulations of ground-penetrating radars over lossy and heterogeneous grounds［J］.IEEE Transactions on Geoscience and Remote Sensing，2001，39(6):1190-1197.

［4］ 張漢華，周智敏，倪宏偉.軌道UWB地表穿透SAR探雷驗證系統［J］.現代雷達，2007，29(2):8-11.Zhang Hanhua，Zhou Zhimin，Ni Hongwei.A rail-mounted UWB ground penetrating SAR landmines detection system［J］.Modern Radar，2007，29(2):8-11.

［5］ Benedetto A，Benedetto F，Blasiis De，et al.Reliability of signal processing technique for pavement damages detection and classification using ground penetrating radar［J］.IEEE Sensors Journal，2005，5(3):471-480.

［6］ 周啟榮.步進頻率探地雷達距離旁瓣抑制研究［D］.長沙:國防科學技術大學，2008.Zhou Qirong.Range side-lobe suppressing of stepped-frequency ground penetrating radar［D］.Changsha:National University of Defense Technology，2008.

［7］ Kositsky J.Results from a forward-looking GPR mine detection system［C］//Proceedings of SPIE.Orlando，FL:SPIE Press，2000:1077-1087.

［8］ Kositsky J，Amazeen C.Results from a forward-looking GPR mine detection system［C］//Proceedings of SPIE.Orlando，FL:SPIE Press，2001:700-711.

［9］ Kositsky J，Cosgrove R，Amazeen C，et al.Results from a forward-looking GPR mine detection system［C］//Proceedings of SPIE.Orlando，FL:SPIE，2002:206-217.

［10］ Bradley M，Witten T，Duncan M，et al.Anti-tank and side-attack mine detection with a forward-looking GPR［C］//Proceedings of SPIE.San Jose，CA:SPIE Press，2004:421-432.

［11］ Liu G，Wang Y，Li J，et al.SAR imaging for a forwardlooking GPR system［C］//Proceedings of SPIE.Orlando，FL:SPIE Press，2003:322-333.

［12］ Rosen E M，Rotondo F S，Ayers E.Testing and evaluation of forward-looking GPR countermine systems［C］//Proceedings of SPIE.Bellingham，WA:SPIE Press，2005:901-911.

［13］ 向道樸.寬帶步進頻率雷達信號源的設計與實現［D］.長沙:國防科學技術大學，2006.Xiang Daopu.Wide-band stepped frequency radar signal source design and realization［D］.Changsha:National U-niversity of Defense Technology，2006.

［14］ 王鵬宇.機載步進頻率SAR成像方法研究［D］.長沙:國防科學技術大學，2008.Wang Pengyu.The imaging research of ultra wideband airborne SAR system using stepped frequency waveforms［D］.Changsha:National University of Defense Technology，2008.

［15］ 陳 波.步進頻率連續波探地雷達數字中頻接收機設計與實現［D］.長沙:國防科學技術大學，2009.Chen Bo.Design and implementation of a digital IF receiver for use in a SFCW GPR［D］.Changsha:National University of Defense Technology，2009.

［16］ Song Qian，Zhang Hanhua，Liang Fulai，et al.Results from an airship-mounted ultra-wideband synthetic aperture radar for penetrating surveillance［C］//The 3rd International Asia-Pacific Conference on Synthetic Aperture Radar.Seoul，Korea:IEEE Press，2011:1-4.

［17］ 方廣有，佐藤源之.頻率步進探地雷達及其在地雷探測中的應用［J］.電子學報，2005，33(3):436-439.Fang Guangyou，Sato Motoyuki.Stepped-frequency ground penetrating radar and it＇s application for landmine detection［J］.Acta Electronica Sinica，2005，33(3):436-439.

［18］ 王 華.步進頻率連續波探地雷達信號源設計與實現［D］.長沙:國防科學技術大學，2009.Wang Hua.Design and implementation of signal source for step frequency continuous wave ground penetrating radar［D］.Changsha:National University of Defense Technology，2009.

［19］ Curtis J O.Electromagnetic power attenuation in soils［M］.Vicksburg:US Army Corps of Engineers，2005.

［20］ Vitebskiy S，Carin L，Ressler M A，et al.Ultra-wideband，short-pulse ground-penetrating radar:simulation and measurement［J］.IEEE Transactions on Geoscience and Remote Sensing，1997，35(3):762-772.

［21］ 李 莎.UWB SFCW-GPSAR系統仿真與校正技術研究［D］.長沙:國防科學技術大學，2009.Li Sha.Research on UWB SFCW-GPSAR system simulation and calibration［D］.Changsha:National University of Defense Technology，2009.

［22］ Wang J，Zhang S H，Liu H W.Integral detecting of low observable target by stepped frequency signals［C］//5th International Conference on Signal Processing Proceedings.Beijing:IEEE Press，2000:1834-1837.

［23］ 龍 騰，李 眈，吳瓊之.頻率步進雷達參數設計與目標抽取算法［J］.系統工程與電子技術，2001，23(6):26-31.Long Teng，Li Dan，Wu Qiongzhi.Design methods for step frequency waveform and the target pick-up algorithm［J］.Systems Engineering and Electronics，2001，23(6):26-31.

［24］ 毛二可，龍 騰，韓月秋.頻率步進雷達數字信號處理［J］. 航空學報，2001，22(增刊):16-24.Mao Erke，Long Teng，Han Yueqiu.Digital signal processing of stepped frequency radar［J］.Acta Aeronauticaet Astronautica Sinica，2001，22(Supplement):16-24.

［25］ 費元春，蘇廣川，米 紅，等.寬帶雷達信號產生技術［M］.北京:國防工業出版社，2002.Fei Yuanchun，Su Guangchuan，Mi Hong，et al.The generating technology of wideband radar signals［M］.Beijing:National Defense Industry Press，2002.

［26］ 王福昌，魯昆生.鎖相技術［M］.武漢:華中科技大學出版社，1997.Wang Fuchang，Lv Kunsheng.Phase locking technique［M］.Wuhan:Huazhong University of Science and Technology Press，1997.

［27］ Steiner M，Kretschmer F F.Missing radar pulse clutter processing［C］//Proceedings of the 1991 IEEE National Radar Conference.Los Angeles，CA:IEEE Press，1991:112-116.

［28］ Narayana S M，Rao G，Adve R，et al.Interpolation/extrapolation of frequency domain responses using the Hilbert transfom［J］.IEEE Transactions on Microwave Theory and Techniques，1996，44(10):1621-1627.

［29］ Sacchi M D，Ulrych T J，Walker C J.Interpolation and extrapolation using a high-resolution discrete Fourier transform［J］.IEEE Transactions on Signal Processing，1998，46(1):31-38.