與美共舞的幾何圖形

Dunelm

幾何學是數學中的重要分支，不僅在科學中有著廣泛的應用，而且對藝術也有重大的影響。歷史上，幾何圖形一直是藝術創作中的重要元素，例如在一千多年前的伊斯蘭教藝術中，我們就能發現許多復雜而精致的幾何圖案。到了近代，伴隨幾何學的不斷發展，我們也能夠欣賞到更多蘊含在幾何學中的藝術之美。

分形幾何：大自然的密碼

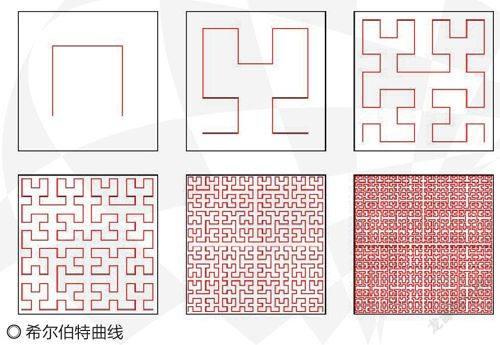
19世紀末20世紀初，數學家們創造了一系列在數學上很奇怪、卻又非常具有美感的幾何形狀。1891年，德國數學家希爾伯特發現了一條可以鋪滿整個空間的曲線，這條曲線被命名為希爾伯特曲線（Hilbert curve）；1904年，瑞典數學家科赫發現了以他名字命名的科赫曲線（Koch curve），又因曲線形似雪花被稱為科赫雪花。

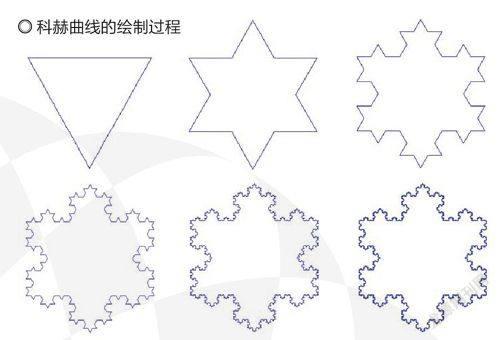
科赫曲線看似復雜，其實畫法很有規律：從一個等邊三角形出發，將每條邊三等分，以每條邊中間的一段為邊向外作等邊三角形，形成一個六角星形。再在六角星形的十二條邊的中間一段上作更小的等邊三角形，并不斷重復這一程序。每一次操作后總長度增加三分之一，而經過無限次操作后就可以得到這個類似雪花的圖形。需要注意的是，科赫曲線的總長度是無限的，但是其面積是有限的。

這些圖形在被創造之初并沒有引起主流數學界的關注，絕大多數數學家認為這些圖形“怪異”、“非自然”，與數學研究沒什么關系。直到1960年，波蘭裔數學家曼德博開始研究這些圖形背后的數學意義，才發現了巨大的價值。1975年，他創造了“分形”（fractal）這個詞來指代這些自相似性的物體，也就是同樣的形狀和圖樣在以不同的規格重復。后人也因此稱他為“分形學之父”。在曼德博看來，自然界充滿了復雜而不規則的結構——如海岸線、山脈、云、冰川、河流系統、星系團等，甚至蔬菜西蘭花，傳統幾何學對此無能為力，而分形學這種新的自然幾何可以大顯身手。此外，在人類生活的很多領域內，例如股票市場的漲跌中也可以發現分形幾何的影子。

在我們的生活中，一個典型的分形例子是河流系統。我們都知道，河流會改道，例如歷史上黃河大的改道就發生過5次。河流改道的原因是河流彎道內側和外側水流的速度有差異，這樣就會對河流造成侵蝕，進而改變河流的平衡并影響河流未來移動的方向。在研究過程中，科學家發現這一過程可以用分形來描述，因此我們又獲得了一個新的視角來觀察河流。

幾何方程：曲線之美

20世紀計算機的出現徹底改變了數學研究。計算機不僅成為輔助數學研究的有力工具，還能讓更多人領略到數學的美。對外行人來說，方程本來只是字母和數字的組合，看起來猶如天書。但是使用計算機，我們可以畫出很多方程對應的曲線，一目了然，還會有意外的驚喜，例如1989年數學家發現的兩種蝴蝶曲線。

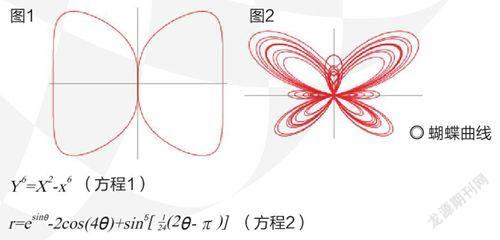
顧名思義，蝴蝶曲線（Butterfly curve）就是曲線形狀如同蝴蝶。第一種蝴蝶曲線如圖1所示，以方程1描述，是一條六次平面曲線。如果大家覺得這個太過簡單，別著急，還有第二種。如圖2所示，以方程2描述，這是一個極坐標方程。通過改變這個方程中的變量θ，可以得到不同形狀與方向的蝴蝶曲線。如果再施以復雜的組合和變換，我們看到的就完全稱得上是一幅藝術品了。

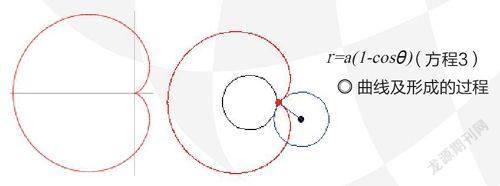
還有一種曲線不得不提，那就是心形曲線（Cardioid curve）。用極坐標表示，這條曲線可以寫成方程3的形式。當一個圓沿著另一個半徑相同的圓滾動時，圓上一點的軌跡就是心形曲線。

關于心形曲線還有一段動人的傳說。法國數學家笛卡兒與瑞典公主克里斯蒂娜邂逅后，兩人相愛，卻遭到瑞典國王的反對。后來笛卡兒染病，臨死前交給公主一封信，信里只有一個方程：r=a（1-cosθ），旁人不解，只有公主明白這是笛卡兒的“一顆心”。這段故事流傳甚廣，國內某著名品牌礦泉水的廣告即取材于此。但實際上，這則故事是后人杜撰而成，唯一真實的地方就是兩人確實相識。

從美好的故事中醒來，我們不必傷感，因為我們知道了原來數學還可以用來表達愛意。不管是蝴蝶曲線還是心形曲線，這些數學王國的精靈也可以像那些名畫一樣，裝飾我們的客廳，裝點我們的生活。

（責任編輯/李平）