多修路，就能解決交通擁堵問題嗎？

曹志剛

現在堵車簡直成了所有城市共同面臨的問題，大城市的擁堵自不必說，連三線城市都開始堵車了。當我們被堵在路上的時候總會想：要是多修幾條路的話，就不會這么堵了吧？事實真的如此嗎？

看似最快捷的路線

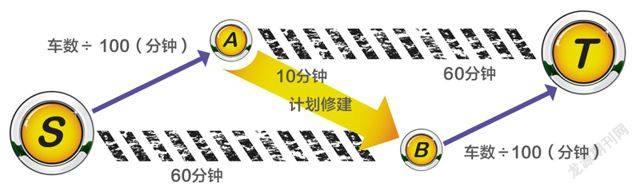
為了研究這個問題，我們設計了一個簡化的交通模型。假設每天有4000人開車從S地到T地去上班。目前有兩條線路供選擇：S—A—T和S—B—T。公路S—B和A—T都比較寬闊，固定耗時60分鐘；公路S—A和B—T則比較窄，耗時由行車數目決定，為車數除以100（分鐘）。

如果是隨機選擇路線的話，時間長了就會摸索出規律，最終的結果是走S—A—T和S—B—T兩條路線的人均為2000人，每個人花費的總時間也都是80分鐘。用學術術語來說，這就是唯一的一個均衡結果。我們用博弈論來預測一定是這個樣子。

如果有一天，政府計劃在A與B之間修建一條快車道。真的很快，只需要10分鐘！這會帶來什么變化？交通擁擠是不是會緩解了呢？

以前走S—A—T路線的人會很高興：因為原來從A到T需要60分鐘，現在先走A—B快車道，再從B到T，最多是10分鐘+4000/100分鐘=50分鐘，至少節約10分鐘！所以這些人都會改走S—A—B—T路線。

以前走S—B—T路線的人也會很高興：因為原來從S到B需要60分鐘，現在先從S到A，再走A—B快車道，最多是4000/100分鐘+10分鐘=50分鐘，至少節約10分鐘！所以這撥人也會改走S—A—B—T路線。

好啦，我們已經分析出來大家都會走S—A—B—T路線。用學術術語來說，這是一個新的均衡。而且皆大歡喜，似乎大家在新均衡下都比舊均衡下少用了10分鐘。且慢，真的是這樣嗎？讓我們再來算一下。如果4000個人都走S—A—B—T路線，那么每個人的總時間應該是4000/100分鐘+10分鐘+4000/100分鐘=90分鐘，這比原來還慢了10分鐘呀！

布雷斯悖論來解釋

究竟是哪種計算正確呢？究竟是變快了還是變慢了？仔細想想就會發現其實是第二種。因為在第一種分析里，原來選擇S—A—T路線的人計算自己節約時間的時候沒有預料到其實另外的人有可能會從S—B轉到S—A，而原來選擇S—B—T路線的人也沒有考慮到有人會從A—T轉到B—T。但是所有人都選擇S—A—B—T的確是唯一的新均衡！在這個狀態下，沒有人愿意改變路線。所以不算不知道，一算嚇一跳。恰恰因為多修了一條路，每個人都要為此而多花費10分鐘！

上述現象是由德國數學家布雷斯（Braess）于1968年首次發現的，我們現在稱之為“布雷斯悖論”。現在有一項相關的科學研究叫“自私路由問題”，是算法博弈論領域的一個前沿研究方向，在交通和互聯網路由方面都有重要應用。

聰明的讀者可能會問，如果真是這樣子的話，那么大家都約定不去走A—B這條近路，而按照原本選擇的路線繼續行進不就沒有問題了嗎？這樣盡管多修了一條路沒有改善交通，但也不至于讓交通變得更糟糕呀！這就涉及到博弈論中的一個經典話題，“囚徒困境”和“集體行動的邏輯”。在某些情況下，合作是件非常困難的事情。說起來容易做起來難呀，即便是有一個好辦法能讓大家都變好，也可能很難實施。每個人都為一己之私著想，每個人做出了一個看起來都聰明無比的決策，卻不去想這樣做會損害別人，最終大家相互損害，達到一個誰都不愿意看到的悲催局面。

生活中的案例

你會不會認為前面舉的例子只是一個數學游戲，僅僅存在于數學家的想象中，現實中絕不可能發生呢？那么親愛的讀者，你又錯了！這樣的例子還真有。在德國的斯圖加特，人們為了改善交通新修了道路，結果卻造成了更加嚴重的堵車，最后不得不廢棄了這條新修建的公路。在 1990 年的世界地球日，紐約市決定關閉第 42 號大街。對堵車泛濫成災的紐約市來說，這個消息簡直是晴天霹靂。就在大家都期待著發生超級大堵車的時候，交通狀況反而難以置信地比平時有所好轉！同樣的事情在韓國首爾的清溪川改造工程中也曾經發生過。

當然，現實的城市交通狀況極為復雜，會受到很多因素的綜合影響，并不是簡單的多一條路少一條路的問題。布雷斯悖論所描述的，也只是一個極端情況。科學家們后來還發現，即便出現了布雷斯悖論，在車流量繼續增加的情況下，交通狀況也會有所恢復，布雷斯悖論將被打破。也就是說，布雷斯悖論只有當車流量在一個固定范圍內時才有可能出現。所以大家請不要太擔心，數學家發現的布雷斯悖論這個“魔鬼”只會在很少的情況下才會困擾我們。

（責任編輯/冷林蔚 劉陽）