蒙特卡羅：從賭城到原子能科學

吳高晨

蒙特卡羅（Monte Carlo）是世界著名的賭城，是摩納哥的標志。起初，蒙特卡羅方法即賭博方法，后來發展成今天非常強大的數學計算方法，可以求解復雜的科學問題。蒙特卡羅方法系統性的研究開始于1944年前后。當時由于研制原子彈，需要研究中子在裂變物質中的運動規律，提出了一些不易用常規數學方法求解的問題。馮·諾依曼、烏拉姆和費米等科學家發展了這個用于直接模擬的蒙特卡羅方法，解決了這些當時不易解決的難題。如今蒙特卡羅方法在原子能科學技術中有著重要的應用。

撒豆子測面積

蒙特卡羅方法是以隨機概率為基礎的方法，在金融工程學、宏觀經濟學、計算物理學等領域應用廣泛。當求解問題是某種隨機事件出現的概率，或者是某個隨機變量的期望值時，通過某種“實驗”的方法，以這種事件出現的頻率估計這一隨機事件的概率，或者得到這個隨機變量的某些數字特征，并將其作為問題的解。

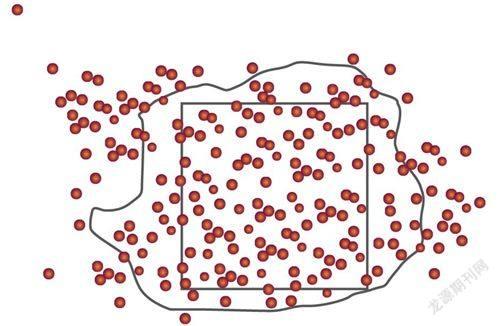
舉一個例子來直觀地了解蒙特卡羅方法：假如我們要計算一個不規則圖形的面積，這個圖形越不規則，就越不容易精確地計算出它的面積，這個時候就可以用上蒙特卡羅方法。假設你有一袋豆子，把豆子均勻隨機地朝這個圖形上撒，然后數這個圖形之中有多少顆豆子，這個豆子的數目就是圖形的面積。不過這個面積只是一個估算值，當你的豆子越小，撒得越多的時候，結果就越精確。所以說，蒙特卡羅方法需要依賴大量的實驗。

利用隨機點計算圓周率

蒙特卡羅方法還可用于估算圓周率，如圖，在邊長為2的正方形內作一個半徑為1的圓，正方形的面積等于2×2=4，圓的面積等于π×1×1=π，由此可得出，正方形的面積與圓形的面積的比值為 4：π。現在讓我們用電腦生成若干組均勻分布0-2之間的隨機數，作為某一點的坐標散布于正方形內，那么落在正方形內的點數N與落在圓形內的點數K的比值接近于正方形的面積與圓的面積的比值，即，N：K≈4：π，因此，π≈4K/N。

用此方法求圓周率，需要大量的均勻分布的隨機數N才能獲得比較準確的數值，這也是蒙特卡羅方法的不足之處。

是原子彈還是反應堆停堆？

眾所周知，核反應堆是一種非常不穩定的存在，因此如何控制核反應堆也就成為原子能科學技術領域非常重要的一個問題。

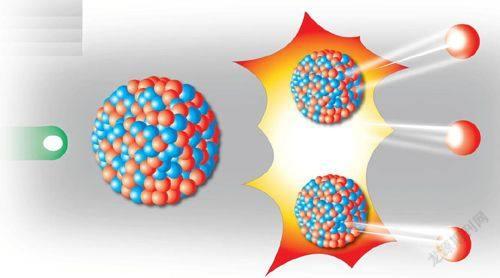
核反應堆的工作原理其實不難理解，一個中子和一個裂變原子核相遇，會發生裂變反應，釋放出能量和兩個以上的中子。這些新產生的中子再去遇到其他裂變原子核，再發生裂變反應。這個鏈條一樣的連續反應被稱為鏈式裂變反應。如果這一切都是原子核自己完成的，就被稱為自持鏈式裂變反應。

大家可能會說，既然一次裂變反應能釋放兩個以上的中子，那反應肯定能夠繼續下去。是的，如果釋放出來的每一個中子都發生了新的裂變反應，裂變反應就會以幾何形式增長，同時釋放出極大的能量。不過如果出現這種情況，我們制造的就不是核反應堆，而是一顆威力巨大的原子彈了。

那么大家又會問，很多國家都建立了核電站，也沒有都變成原子彈啊。是的，那是因為反應堆中不是只有裂變原子核，還有其他大量的材料，這些材料會吸收掉一些中子，還會有一些中子泄漏到反應堆外，造成中子數的減少。如果中子數減少的數量大于增加的數量，最終反應堆會停止運行，被稱為停堆。

只有當中子增加的數量與減少的數量相當時，反應堆才能處于一種臨界安全狀態。蒙特卡羅方法就可以幫助科學家計算和控制這個狀態。

為什么要用蒙特卡羅方法呢？因為中子和裂變原子核在不同的時間具有不同的能量狀態、不同的位置、不同的飛行方向，常規數學方法幾乎無法計算這一復雜的多維問題。這種雜亂無章的具有統計性質的運動方式正好符合蒙特卡羅方法的思想。蒙特卡羅方法關注中子的運動軌跡，跟蹤記錄一個中子產生了幾個新的中子，把結果通過計算機記錄下來，等這個中子消失后，轉頭去跟蹤下一個目標。我們把計算機追蹤過的中子數稱為N，那么反應堆中消失的中子數就是N；而把計算機監測到的新產生的中子數稱為M，當N=M時，則核反應堆處于臨界安全狀態。

蒙特卡羅方法不僅在原子能科學中大量使用，目前在軍事科學、氣象科學、醫學、地質學等領域均已廣泛使用。蒙特卡羅方法在近30年來之所以能有這樣大的發展，與計算機的快速發展和廣泛使用是密不可分的。凡用蒙特卡羅方法求解一個問題時，往往需要進行大量的重復一個過程，這一過程要靠計算機才能完成。如果要求計算結果的誤差越小，所進行的重復過程應越多，因此計算量相當大，沒有現代的計算機技術，很難設想蒙特卡羅方法會有今天的發展，可以預料，隨著計算機技術的進一步發展，蒙特卡羅方法將會有更大的發展。

蒙特卡羅方法的發明人

烏拉姆是蒙特卡羅方法的發明人之一，美國數學家。他曾參與美國原子彈研制工程—曼哈頓工程，第二次世界大戰后又參與了氫彈研制工程。他曾當選為美國總統科學顧問委員會成員、美國藝術與科學學院院士、美國全國科學院院士。烏拉姆參與提出的蒙特卡羅法，當時被用于核物理研究，現已被廣泛地使用到許多領域。