室內(nèi)雕塑點云三維重構(gòu)

香玫元，李 赟，艾海濱，張 力

(1.蘭州交通大學，蘭州 730070；2.中國測繪科學研究院，北京 100830)

1 引言

目前，室內(nèi)三維導航定位正在迅速的發(fā)展，三維模型對于室內(nèi)三維導航定位有著至關(guān)重要的作用，直接影響著用戶使用體驗感，而其中一些場景往往含有雕塑，如博物館、大型商場等。室內(nèi)雕塑的三維建模是一項費時費力的工作，常用的方法是用三維構(gòu)建軟件(如3ds max，Maya等)，由人工手動構(gòu)建，這不僅非常耗時，并且大大提高了成本。所以，室內(nèi)雕塑三維模型構(gòu)建急切需要一種自動建模方法。在此領(lǐng)域，國內(nèi)外研究者提出了多種三維建模的方法。文獻[1]針對當前常用的計算機建筑建模方法，對三維(3D)建模技術(shù)和建模方法作了系統(tǒng)、全面、深入的分析。文獻[2]利用三維激光掃描技術(shù)進行建筑物室內(nèi)外一體建模方法研究，為室內(nèi)外場景三維重建提供了有效方法。文獻[3]利用三維激光點云數(shù)據(jù)和圖像信息來實現(xiàn)對室內(nèi)場景的三維重建，為未知環(huán)境下的移動機器人導航提供輔助。本文利用已有的離散點云數(shù)據(jù)，對其預處理，然后進行三維模型構(gòu)建，可以快速得到雕塑三維幾何模型。

2 點云數(shù)據(jù)的預處理

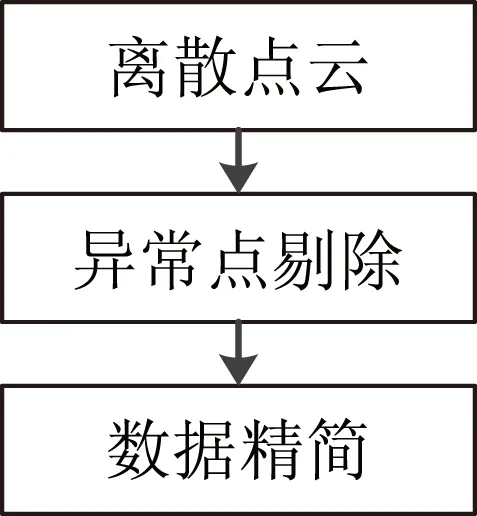
圖1 數(shù)據(jù)預 處理流程

由于使用不同的測量方法，測量設(shè)備存在缺陷，獲得到的點云數(shù)據(jù)通常不可避免地存在一些問題，包括噪聲點的產(chǎn)生、數(shù)據(jù)失真和數(shù)據(jù)冗余等問題。帶有許多雜點、噪聲點的點云數(shù)據(jù)會影響后續(xù)的曲面重構(gòu)過程，就需要進行異常點剔除；另外，各種測量方法的速度不斷加快，效率不斷提高，測量產(chǎn)生的點云數(shù)據(jù)量往往非常龐大，所以需要進行數(shù)據(jù)精簡。因此，在曲面重構(gòu)前，需要對點云進行一些必要的處理，以獲得滿意的數(shù)據(jù)，即點云預處理。主要包括：異常點剔除、數(shù)據(jù)精簡。預處理流程如圖1所示。

2.1 異常點剔除

點云數(shù)據(jù)上的異常點，可能使該點及其周圍的曲面片偏離原曲面，使得重構(gòu)獲得的幾何模型與物體的真實模型不一致，所以必須對原始點云數(shù)據(jù)進行預處理，以剔除異常點。不同測量方式得到的點云數(shù)據(jù)的呈現(xiàn)方式各不相同，根據(jù)點云中點的分布特征將點云分為：散亂 點云、掃描線點云、網(wǎng)格化點云。實際工程中常用的是散亂點云和掃描線點云，本文中使用的數(shù)據(jù)為離散點云數(shù)據(jù)。找出并剔除異常點的判斷方法主要是：首先計算所有點云到他們的k最近鄰的平均平方距離，然后根據(jù)計算到的平均平方距離對點云進行升序排列，最后剔除其中最大值的點。異常點剔除效果如圖2所示。

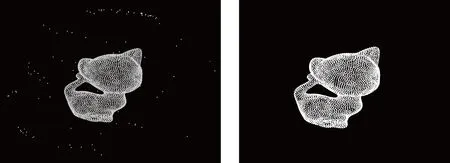
圖2 原模型(左圖)與經(jīng)過異常點剔除后的模型(右圖)

2.2 數(shù)據(jù)精簡

通常在數(shù)據(jù)測量時，為了盡可能地獲得更多的表面細節(jié)，最終得到的點云數(shù)據(jù)通常數(shù)據(jù)量較大，并且可能存在大量的冗余。為了提高曲面重建的效率和質(zhì)量，需要按一定的要求減少點云的數(shù)量，即進行數(shù)據(jù)精簡。本文中首先使用體包圍盒來約束點云，然后將體包圍盒分解成若干個大小相等的小包圍盒，最后在每個小包圍盒中選取最靠近包圍盒中心的點來代替整個包圍盒中的點。數(shù)據(jù)精簡效果如圖3所示。

圖3 原模型(左圖)與經(jīng)過數(shù)據(jù)精簡后的模型(右圖)

3 三維模型重構(gòu)

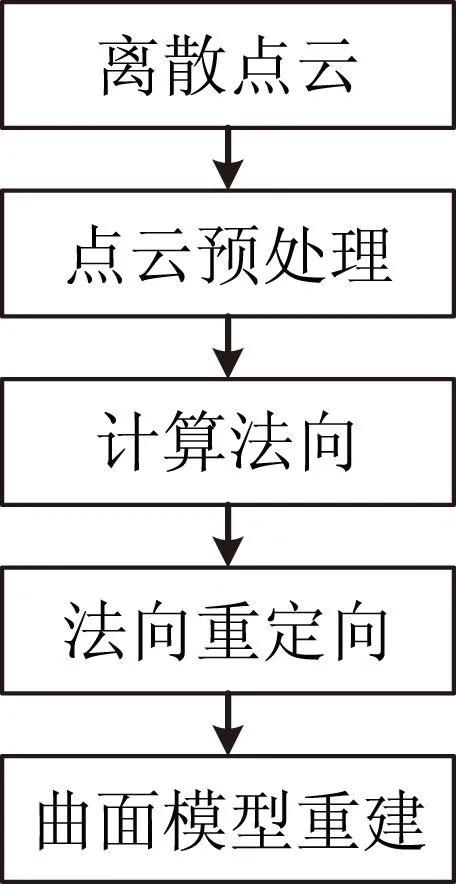
圖4 三維模型 重建流程

三維模型的曲面重建是幾何造型中的一個重要研究領(lǐng)域。曲面重建的是為了恢復實物模型的曲面形狀，并且使得模型的形狀盡可能地反映現(xiàn)實實物的形狀特征。根據(jù)重建曲面的表現(xiàn)形式不同，可以將曲面重建方法分為參數(shù)曲面重建、多面體網(wǎng)格重建、細分曲面重建和隱式曲面重建等。本文選用的是隱式曲面重建中的泊松曲面重建方法[4]。泊松曲面重建方法的優(yōu)點是抗噪性好，受非均勻采樣影響小，重建結(jié)果光滑，并可以控制結(jié)果的光滑與精細程度。泊松曲面重建方法需要知道點數(shù)據(jù)的法方，所以在曲面重構(gòu)前需要計算法向，并對法向重定向盡可能地確保法向的正確。三維模型重建流程如圖4所示。

3.1 法向估計

點的法向是泊松曲面重建必不可少的信息。點云法向估計的可靠性對于曲面重建質(zhì)量很重要。點云法向估計越可靠，曲面重建質(zhì)量越高。目前已有的法向估算方法可分為基于 Delaunay/Voronoi劃分的方法、基于局部表面擬合的計算方法和基于魯棒統(tǒng)計的方法。其中基于局部表面擬合的計算方法主要是主元分析(principal component analysis，PCA)估算方法[5]，以及在PCA基礎(chǔ)上的一些改進方法。本文中估算點法向采用PCA估算方法。

PCA原理為：假定點集Np是點p的鄰域點集，其3×3協(xié)方差矩陣C定義為：

(1)

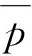
C·νI=λI·νI,I∈{0,1,2}

(2)

協(xié)方差矩陣是一個矩陣，其每個元素是各個向量元素之間的協(xié)方差。協(xié)方差矩陣C是對稱半正定矩陣，所以特征值λI是實數(shù)，并且特征向量νI形成一個正交坐標系，與由Np定義的點集的元主成分一致。

λI表示pi，i∈Np沿與λI相應的特征向量方向的方差大小。這樣就可以計算出總方差值，也就是pi到它們的重心之間的距離平方和，可表示如下：

(3)

假設(shè)λ0≤λ1≤λ2，滿足這樣一個平面

(4)

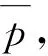
這樣，協(xié)方差矩陣C最小特征值的特征向量可被作為點p的法向量。通過這種方法就能夠得到所有點的法向量。

3.2 法向重定向

求出每個點的法向量之后，還需要對法向量的方向進行調(diào)整，使得所有法向量都指向模型的外側(cè)。因為在泊松曲面重建中法向量本身的精確度并不是很重要，重要的是通過法向量的方向來區(qū)分模型的內(nèi)側(cè)和外側(cè)。

算法中認為每個點和它的最近鄰的法向量方向差別不大，所以它們的法向量內(nèi)積應該是大于0的。這樣就可以通過判斷一個點的法向量和它的最近鄰的法向量方向內(nèi)積是否大于0決定是否應當調(diào)整它的法向量的方向。

具體實現(xiàn)的方法就是先找到圖形的最低最左點，容易看出這一點的法向量應當指向Z坐標為負的方向。這一點的法向量方向調(diào)整好以后，就可以對所有的點建一棵最小生成樹，以最低最左點為根深度優(yōu)先地遍歷整棵樹，并根據(jù)每個頂點在樹中的父節(jié)點調(diào)整其法向量的方向。通過這樣的調(diào)整，就可以得到在全局意義上一致的法向量。

3.3 曲面重建

室內(nèi)雕塑點云模型往往對重建結(jié)果的準確性及細節(jié)方面要求很高。泊松重建方法作為一種經(jīng)典的隱式重建方法，在已知點云精確法向量的基礎(chǔ)上，能高效處理上述問題，同時能生成不同表示層次上的模型，滿足室內(nèi)導航中精細模型的要求。泊松重建主要是通過對點云數(shù)據(jù)進行最優(yōu)化的插值處理來獲得近似曲面。

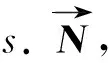
首先需要定義梯度場。由于梯度函數(shù)是一個分段常函數(shù)，其函數(shù)值發(fā)生了突變，對梯度場的顯式計算會導致在曲面邊界處產(chǎn)生無窮大的情況。為了處理這種情況，需要用指示函數(shù)和一個平滑濾波函數(shù)進行卷積，然后考慮平滑后的梯度場。

然后需要估計向量場。因為不知道模型表面的幾何特征，不能近似地計算模型的曲面積分。輸入的帶法向的有向點集提供了精確的信息，可以通過離散求和來近似計算模型的曲面積分。根據(jù)點集S把?M分割成不同的小面片Ps??M，則可以根據(jù)點s.p的值與小面片的面積的乘積來近似計算小面片上的積分：

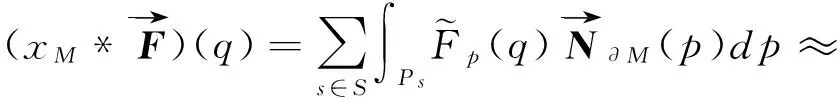
(5)

最后將三維重建的問題轉(zhuǎn)化為求解泊松方程。

4 實驗結(jié)果與分析

針對上述方法，對兩組數(shù)據(jù)進行三維重構(gòu)，以下給出具體的實驗結(jié)果。表1列出了在重構(gòu)過程中的一些相關(guān)數(shù)據(jù)，計算時間是從讀入原始點數(shù)開始，經(jīng)過預處理后生成三維模型的時間。從表1的結(jié)果可以看出采用泊松曲面重建方法對離散點云數(shù)據(jù)的重建可以得到較好的結(jié)果，所耗費的時間都不是很大。圖5是對大量數(shù)據(jù)點集貓的重構(gòu)結(jié)果，圖6對大量數(shù)據(jù)點集獅子的重構(gòu)結(jié)果。從得到的結(jié)果可以看出：泊松曲面重建方法雖然使得有些細節(jié)表現(xiàn)不夠細致，但是能很好的擬合模型表面，并且在離開表面處不會形成其它錯假面片，得到的重構(gòu)模型表面的光順性很好。

表1 試驗相關(guān)數(shù)據(jù)

圖5 貓的模型

圖6 獅子的模型

5 結(jié)論

結(jié)合已有離散點云數(shù)據(jù)，給出了一種從點云數(shù)據(jù)到三維幾何模型的方法。實驗表明本文的方法建模速度快，表面能夠很好的擬合，異常點對建模影響較小，得到的重構(gòu)模型表面的光順性很好，可以滿足室內(nèi)模型的生成。但是還存在一些問題有待解決：方法對于模型表面的一些細節(jié)處理的不夠理想；模型邊緣過于平滑；重構(gòu)后的模型還需要進一步優(yōu)化。

[1] 雷鴻源，陳熾坤，王高.建筑室內(nèi)計算機建模方法的探討[J].工程圖學學報，2005(5)：23-28.

[2] 楊林，盛業(yè)華，王波.利用三維激光掃描技術(shù)進行建筑物室內(nèi)外一體建模方法研究[J].測繪通報，2014(7)：27-30.

[3] 張勤，賈慶軒.基于激光與單目視覺的室內(nèi)場景三維重建[J].系統(tǒng)仿真學報，2014，26(2)：357-362.

[4] KAZHDAN M，BOLITHO M，HOPPE H.Poisson Surface Reconstruction[EL/OL].[2014-08-10].http：//web.cs.jhu.edu/～bolitho/Research/PoissonSurfaceReconstruction/PoissonRecon.pdf.

[5] SANGVERAPHUNSIRI V，SRITRAKULCHAI K.The Development of a Technique for 3D Complex Surface Reconstruction from Unorganized Point Cloud[J].The International Journal of Advanced Manufacturing Technology，2007，33(7)：772-781.

[6] PUALY M.Point Primitives for Inteacrtive Modeling and Proeessing of 3D Geometry[D].Zurich:Federal Institute of Technology(ETH) of Zurich, 2003.

[7] 路興昌，宮輝力，趙文吉，等.基于激光掃描數(shù)據(jù)的三維可視化建模[J].系統(tǒng)仿真學報，2007，19(7)：1624-1629.

[8] 白成軍，吳蔥.文物建筑測繪中三維激光掃描技術(shù)的核心問題研究[J].測繪通報，2012(1)：36-38.

[9] 鄧志東，牛建軍，張競丹.基于立體視覺的三維建模方法[J].系統(tǒng)仿真學報，2007，19(14)：3258-3262+3289.

[10] 周儒榮，張麗艷，蘇旭，等.海量散亂點的曲面重建算法研究[ J].軟件學報，2001，12(2)：249-255.