齒輪傳動副背隙動態測試平臺的仿真與研究

王 剛，盧 紅，石立城

（武漢理工大學機電工程學院，湖北 武漢430070）

當一對齒輪嚙合時，輪齒非嚙合面的兩個輪齒之間存在回程間隙，這嚴重影響了傳動精度和性能，為此，設計搭建一個傳動性能測試實驗臺，主要分析比較可替換的行星齒輪傳動和蝸輪蝸桿傳動機構，測試研究機械傳動系統的性能。齒輪傳動和蝸輪蝸桿傳動都是回轉傳動，在有些場合可以互換使用，但同時它們又各自具有自身的特點，在設計過程中需要根據實際的情況進行比較選擇以保證傳動形式最為可靠精準。目前研究現狀是:兩種傳動方式的實驗平臺的振動、傳動背隙、振動特性等屬性不是特別清晰，內部規律還需進一步深入研究，本文以此為研究對象，用solidworks建模，使用有限單元法，比較了相同精度和尺寸大致相當條件下，這兩種傳動方式的一些模態、諧響應特性［1－2］。

1 蝸輪蝸桿和行星齒輪測試實驗平臺

本文設計建模，并用有限元分析為后續實驗驗證比較提供理論依據，并且將理論和實際進行匹配比較。為了比較齒輪傳動系統與蝸輪蝸桿傳動系統的差別，選取同樣精度等級和相近大小尺寸的兩套系統（圖1、圖2）。本實驗用來比較兩種傳動方式在實際應用中的優劣，驗證仿真的可靠性，為此搭建一個試驗，實現方式為:驅動電機正轉提供動力，負載電機被動反轉模擬負載，具體通過加載試驗，測試不同轉速、轉矩下傳動系統振動、噪聲等參數。通過噪聲儀測量實驗臺的噪聲分貝數來判斷振動的強弱；在支架上粘貼應變片，測量應力變形情況來評估振動及其傳動系統的穩定性。通過電氣控制，使齒輪在起動和換向的過程中始終受到偏置力矩的作用，編碼器讀取脈沖反饋，半閉環控制，對誤差進行實時補償，實現無回差反轉，從而達到消除背隙。檢測比較傳動機構隨負載變化而變化的振動頻率，傳動精度，以及控制策略［3－4］。

圖1 直線式布局

圖2 垂直式布局

2 蝸輪蝸桿和行星齒輪接觸應力分析

理論上沒有背隙的齒輪應該也能傳動，正因為齒輪在傳動中會變形，才需要背隙。背隙與載荷關系曲線幫助用戶判斷加載之后的間隙與磨損，平衡取舍。而額定載荷下齒面變形量則可以反映由載荷造成背隙的影響，進而判斷兩種減速器的優劣。

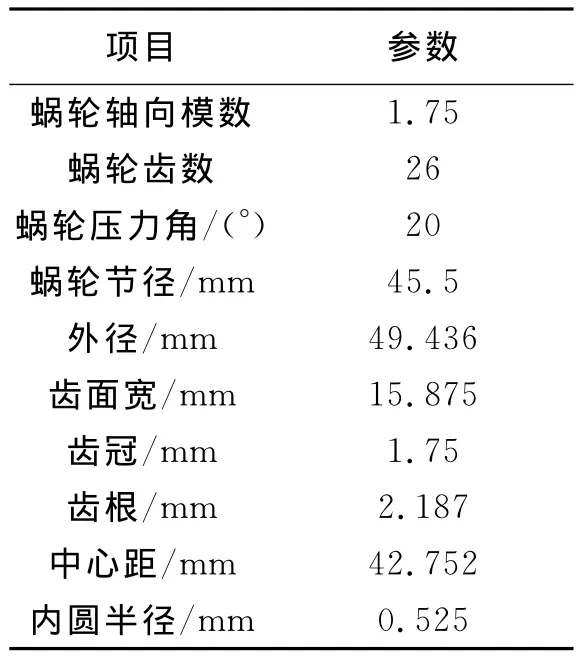
表1 蝸輪尺寸參數

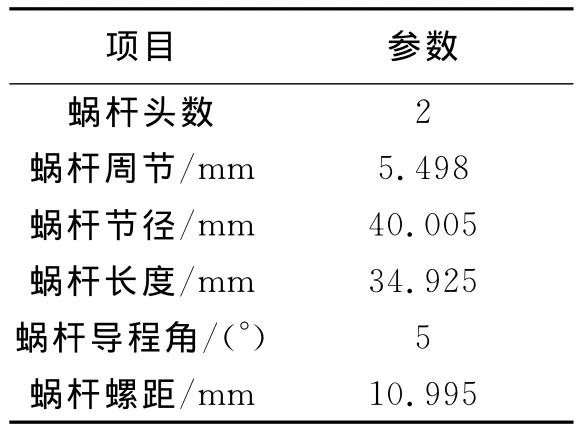
表2 蝸桿尺寸參數

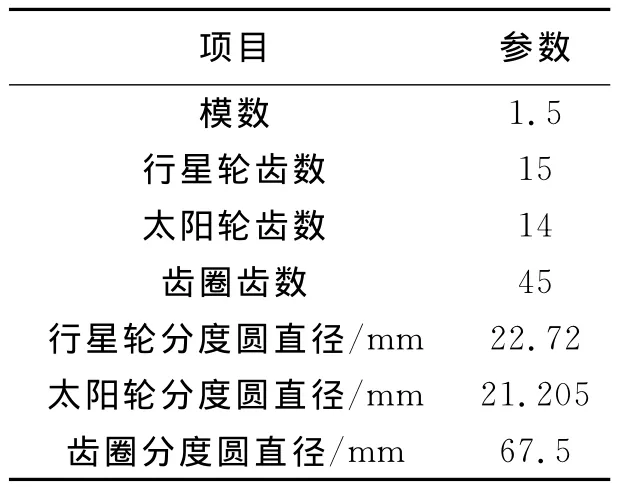
表3 星齒輪尺寸參數

在此，對以上蝸輪蝸桿［5－6］（表1、表2）和行星齒輪［7－8］（表3）進行了裝配體導入、材料屬性定義、邊界接觸條件定義、網格劃分（見圖3、圖4）、施加約束、求解器定義等操作。其中材料為45號鋼（調制），彈性模量E ＝200GPa，泊松比u＝0.3；根據實際工況在蝸輪蝸桿和行星齒輪輸入軸施加2.6 Nm轉矩。

圖3 蝸輪蝸桿網格劃分

圖4 行星齒輪網格劃分

圖5 蝸輪蝸桿等效應變

圖6 行星齒輪等效應變

從圖5、圖6的應力應變云圖可以分析出，在力矩傳遞過程中，齒廓之間會有很大的應力出現，但由于齒廓的強度較高，應變較小。然而每一個應變的疊加就會造成傳動過程中的背隙出現，降低傳動精度，引起振動和噪聲，而且隨著齒廓表面的磨損，背隙現象會越來越嚴重。

比較二者最大等效應變，行星齒輪明顯小于蝸輪蝸桿。由此可以比較得出:無論從形變量，還是最大應力應變，行星齒輪都比蝸輪蝸桿性能優越；因此，由轉矩產生的背隙，行星齒輪更少，性能更加優越。

3 模態分析

模態是機械結構的固有振動特性，每一個模態具有特定的固有頻率、阻尼比和模態振型，找到結構振動的一些基本振型對應的頻率，避開這這些基本頻率，防止共振。

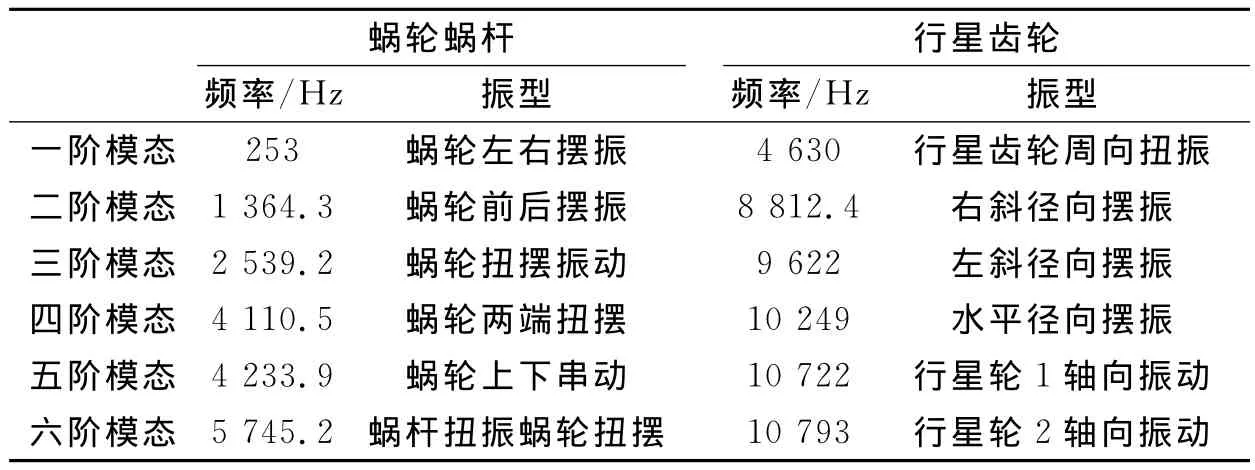
表4 行星齒輪－蝸輪蝸桿一至六階振型頻率

從表4可以看出無論從各階的振型還是變形量，行星齒輪減速器都比蝸輪蝸桿減速器優越，因為從結構上分析，行星齒輪為斜齒輪，并且對稱性非常好，可以有效地削弱振動。

4 諧響應分析

諧響應分析建立在模態分析的基礎之上，是用于確定線性結構在承受一個或多個隨時間按正弦規律變化的載荷時，穩態響應的一種技術。諧響應分析的目的在于計算出結構在幾種頻率下的響應值對頻率的曲線，從而使設計人員能預測結構的持續性動力特性，驗證設計是否能克服共振、疲勞以及其他受迫振動引起的有害效果。

4.1 諧響應分析操作

從靜態結構到模態分析到諧響應分析，材料屬性和幾何模型進行共享，并且對模型，設置，求解器進行設置。設置參數為:蝸輪蝸桿輸入軸施加2.6 Nm轉矩，蝸桿嚙合面為檢測平面，計算頻率為從200Hz到4 000Hz，步長為50Hz；行星齒輪太陽輪輸入軸孔中施加2.6Nm轉矩，輸出軸太陽輪軸為檢測體，計算頻率從4 000Hz到10 000Hz，步長為100Hz.

4.2 蝸輪蝸桿諧響應結果

圖7為蝸輪蝸桿應力頻譜和位移頻譜。顯然在頻率為950Hz和2450Hz的時候，位移速度，應變和加速度有兩個峰值。

圖7 應力頻譜（上）-位移頻譜（下）

下面分別計算這兩個頻率值時候的位移形變和等效應應力。由圖8可見:在950Hz的時候，蝸桿的諧響應振幅達到最大，為3.1964×10－5m，振動形式為蝸桿兩端反向斜擺，最大振動位置發生在輸入端；由圖9可見:在2 450Hz的時候，蝸桿的諧響應振幅達到最大，為2.1688×10－4m，最大應力為6.688×108Pa，振動形式為蝸桿兩端同向扭擺，最大振動位置發生在輸出端；比較兩圖，第二種振動更加劇烈，與前面分析一致，并且容易引起齒輪箱體的嚴重振動。

圖8 總體變形圖1

圖9 總體變形圖2

4.3 行星齒輪諧響應結果

圖10 為諧響應分析的應力頻譜和位移頻譜。顯然在頻率為4 600Hz和7 150Hz的時候，應力有兩個峰值。

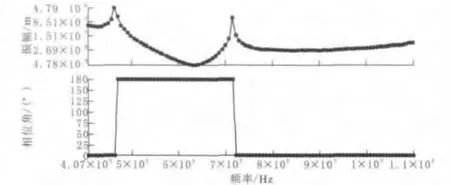
圖10 應力頻譜（上）-位移頻譜（下）

1）分別計算這兩個頻率值時候的位移形變。由圖11可以看出:在4 600Hz的時候，行星齒輪的太陽輪諧響應振幅達到最大，為1.7788×106m，最大應力為5.554×108Pa，振動形式為太陽輪軸向串動，最大振動位置發生在太陽輪齒輪嚙合處。

2）由圖12可以看出:在7 150Hz的時候，行星齒輪的太陽輪的諧響應振幅達到最大，為7.927×104m，最大應力為4.257×109Pa，振動形式為太陽輪回轉振動，最大振動位置發生在齒輪嚙合處。

圖11 總體變形1

圖12 總體變形2

5 結論

1）應變的疊加就會造成齒側背隙，降低傳動精度，而且隨著齒廓表面的磨損，背隙現象會越來越嚴重；無論從形變量，還是最大應力應變，行星齒輪都比蝸輪蝸桿性能優越。

2）行星齒輪減速器振動頻率比蝸輪蝸桿高，遠離正常工作頻率，并且抗振動效果比蝸輪蝸桿減速器好；在機器正常工作頻率區間，要遠離計算出的峰值頻率，啟動的時候不能長期停留在振動加強頻率區間，正常工作時要選擇振動比較低且比較平穩的工作頻率區間。根據理論頻率曲線和對應振型可以提前預知實際振動形式，為搭建實驗平臺提供了數據。

［1］ 常 遠，甄萬才.齒輪傳動與蝸輪蝸桿傳動性能比較與消隙機構［J］.電子工業專用設備，2007（01）:1-3.

［2］ Baek J.Backlash estimation of a seeker gimbal with two-stage gear reducers［J］.The International Journal of Advanced Manufacturing Technology 21.8（2003），2003，1（01）:1-2.

［3］ Merzouki R，CadiouandN J C.Sirdi M.Compensation of backlash effects in an Electrical Actuator［J］.LaboratoiredeRobotiquedeVersailles 10-12，avenue de l’Europe.2:2-3.

［4］ 王汝青，陳興燕，盧 利.基于ANSYS的非對偶蝸輪蝸桿不同嚙合位置有限元分析［J］.科技廣場，2012（05）:6-9.

［5］ 邱 晶 .基于ANSYS環境下的TI蝸桿建模分析與安裝誤差分析［D］.天津:天津大學，2006.

［6］ 李俊源.基于SolidWorks的蝸輪蝸桿三維參數化設計［J］.長春理工大學學報，2006，29（01）:2-3.

［7］ 劉雪艷.基于ANSYS的漸開線直齒行星齒輪有限元分析［D］.西安:西北農林科技大學，2009.

［8］ 王春光.行星齒輪傳動動態特性的研究［D］.哈爾濱:哈爾濱船舶鍋爐渦輪機研究所，2005.