關于軸承預緊力對軸系性能影響的仿真分析

李頌華，馮明昊

（沈陽建筑大學 交通與機械工程學院，遼寧 沈陽 110168）

0 引言

主軸系統是機床的核心功能部件之一。對主軸軸承施加預緊力不僅能夠消除軸承的軸向間隙，降低振動噪聲，提高支承體旋轉精度，控制滾動體的自旋滑動，減少滾動體的公轉打滑，進而提高軸系剛度，降低軸系振動，而且還能夠提高主軸系統的臨界轉速和機床的加工精度。然而，軸承預緊力施加的太大就會加劇軸承發熱，降低軸承的使用壽命并引起主軸溫升和熱變形的增大，尤其是在主軸高速旋轉時這種狀況會更加明顯；軸承預緊力施加的太小又不能充分發揮主軸系統的潛能[1]。因此，關于軸承預緊力的研究對提高主軸系統的綜合性能具有重要意義。

本文對不同預緊力下的軸承剛度進行了理論計算，并對不同預緊力下的主軸軸承系統進行了模態和諧響應分析。

1 軸承剛度的理論計算

根據機床的不同類型，高速主軸軸承具有多種配置方式，實驗室對原有磨削電主軸進行了軸承預緊力施加改造，如圖1 所示。主軸前后端各配置一個軸承，采用背對背配置方式。使用壓電陶瓷微位移驅動器對軸承施加預緊力，采用應變片壓力傳感器檢測所施加軸承預緊力的大小，使用熱電偶檢測軸承的溫升。

圖1 電主軸軸承預緊力施加結構圖

角接觸球軸承在軸承預緊力Fp的作用下，接觸角由α0變成α1，計算公式[2]為：

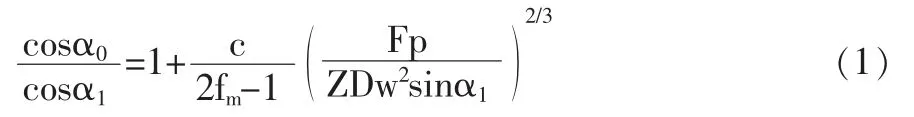
式中： c—接觸變形因數；fm—內外滾道曲率比的平均值，fm=（ri+re）/（2Dw）；α0—初始接觸角；α1—變形后的接觸角；DW—軸承滾珠直徑；Z—軸承滾珠數量。將式（1）轉變為：

本文的電主軸采用7009C 軸承，初始接觸角為15°。式（2）等號右側能夠根據相關參數直接計算得出，等號左側的α1通過迭代計算，進而求出軸承施加預緊力之后的接觸角。軸承軸向和徑向剛度通過公式 （3）～（5）[2]計算：

式中： Fa和Fr—軸承的軸向和徑向載荷。為了方便計算，本文使用VB6.0 編寫了相應的計算程序軟件，以便快速計算出了在不同預緊力下軸承的軸向剛度和徑向剛度，如表1 所示。從表中可以看出，軸承的軸向和徑向剛度都隨軸承預緊力的增加而增加。

表1 預緊力與軸承剛度

2 模型的建立

求出預緊力與軸承剛度的關系后，本文利用有限元法對軸系進行模態和諧響應分析。由于是對同一軸系進行分析，所以諧響應分析與模態分析模型完全相同。

在軸系有限元模型中將軸承模擬為彈簧單元，通過設置不同預緊力下的軸承剛度值，運用靜力學分析求解軸系的固有頻率。有限元建模過程[3]如下：

（1）主軸預處理。將孔、槽和螺紋等按實體處理，將各處倒角簡化為直角，忽略空刀槽，在不影響計算結果的前提下保證網格模型的規則劃分和可求解性。

（2）附加質量的處理。將電機的轉子及平衡環等效為同密度軸材料，作為主軸的附加分布質量，等效到所在單元的節點上[4]。

（3）軸承等效處理。每個軸承可等效為4 個軸向分布和4 個徑向分布的彈簧單元，如圖2 所示。彈簧的長度為軸承內、外半徑之差，位置點在軸承法線與主軸中心線的交點。彈簧單元參數有剛度（軸承的軸向剛度Ka與徑向剛度Kr）和阻尼。

（4）軸系有限元模型建立和網格劃分。選取合適網格的劃分尺寸，在主軸某一半剖面內用平面單元（如PLANE42）進行網格劃分；再通過旋轉用三維實體結構單元 （如SOLID45） 進行網格劃分。

（5）如圖3 所示，將彈簧單元的外接點全部固接。

圖2 軸承的等效處理

圖3 軸系有限元模型

3 軸系固有頻率的仿真計算

3.1 固有頻率仿真計算的理論基礎

模態分析用來確定結構或構件的振動特性，即固有頻率和振型[5]。為了能更好地進行理論分析，必須建立能夠真正反映振動系統實際情況的動力學模型和對應的數學模型，再根據數學模型求解系統的特征向量初特征值（固有頻率）。多自由度的運動微分方程：

式中： M、C、K—系統的質量、阻尼、剛度矩陣；x11（t）—系統的振動加速度矩陣；x1（t）—系統的振動速度矩陣；x（t）—系統的振動位移矩陣；F（t）—系統的載荷向量矩陣。

當F=0 時，求解齊次方程得到的通解將反映系統的自由振動特性，求解它所對應的特征方程得到系統特征解將反映結構的固有特性。

當F≠0 時，求解非齊次方程得到方程的特解將反映輸入載荷的特點。

固有頻率只與系統本身特性有關，當外載荷F（t）=0時，系統的微分方程：

求解微分方程的廣義特征值便是系統的固有頻率。

3.2 固有頻率分析計算

在ANSYS 中有多種模態提取方式，本文采用Block Lanczos 法。Block Lanczos 法功能強大，尤其對于提取大型模型中的大量振型非常有效。它經常應用在具有實體單元或殼單元的模型中，在具有或沒有初始截斷點時同樣有效（允許提取高于某個給定頻率的振型），還可以很好的處理剛體振型。

軸承在不同預緊力下擁有不同的軸向和徑向剛度，進而對軸系的固有頻率有不同的影響。本文首先計算出軸承在不同預緊力下的軸向和徑向剛度，在對模型中模擬軸承的彈簧施加不同的剛度，最終獲得不同預緊力下軸系的固有頻率。軸系在不同預緊力下有多階固有頻率，本文只考慮一階頻率。計算結果如圖4 所示。從圖中可以看出，軸系的一階頻率隨著軸承預緊力的增大而增大。同時隨著軸承預緊力的增大，軸系一階頻率的增長速度變慢。說明對軸承施加預緊力能夠提高軸系的固有頻率。這為為提高軸系臨界轉速而選擇軸承預緊力大小提供理論參考。

圖4 軸承預緊力與軸系固有頻率

4 軸承預緊力對軸系振動的影響

4.1 諧響應分析理論基礎

諧響應分析是用于求解一個線性結構在已知頻率的正弦載荷作用下結構穩態相應的技術。該技術只計算結構的穩態受迫振動，不考慮結構在激勵開始時的瞬態振動。諧響應分析預測結構的持續動力特性，從而能夠驗證此結構是否能夠克服疲勞共振及其他受迫振動引起的有害影響。

諧響應分析為輸入諧波載荷（力、壓力和強迫位移），輸出每一個自由度上的諧響應（如位移、應力和應變等），其動力學運動方程：

式中：[M]—質量矩陣；[C]—阻尼矩陣；[K]—剛度矩陣；{u11}—節點加速度向量；{u1}—節點速度向量；{u}—節點位移向量；{F（t）}—載荷為時間的任意函數。對簡諧運動而言，{u}和{F}均為簡諧形式，設其頻率為ω，則有：

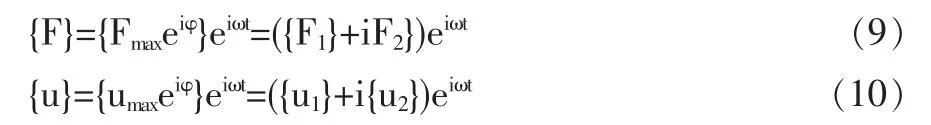
將式（9）和（10）代入式（8），可得諧響應分析的運動方程：

由此可見，當所施加載荷的虛部非零時，諧響應分析得到的響應解均是復數形式。

4.2 諧響應分析計算

在ANSYS 中有三種諧響應分析方法： 完全法、縮減法和模態疊加法。其中模態疊加法通過對模態分析得到振型（特征值），再乘上系數并求和，來計算結構的響應，并且計算速度快。本文的采用模態疊加法進行諧響應分析計算。

在激振力的作用下，軸系在其固有頻率處會發生共振并產生響應位移。本文對不同預緊力下軸系一階頻率的響應位移進行了計算分析，選取的激振力Fr=100N，在主軸前段加載。

圖5 主軸前段徑向響應位移

圖5 是軸系在不同預緊力作用下，主軸前段、主軸后端和主軸中間的徑向響應位移。從中可以看出，主軸前段和后端的徑向響應位移隨著軸承預緊力的增大而降低且降低速度逐步減小；主軸中間的徑向響應位移隨著軸承預緊力的增大而增大且增長速度減慢。說明對軸承施加預緊力能夠降低主軸前段和后端的振動，同時也會提高主軸中間的振動。這為軸系的優化設計提供理論參考。

5 結論

基于實驗室的磨削電主軸完成了不同軸承預緊力下軸承剛度的計算，并對磨削電主軸軸系在不同軸承預緊力下進行了模態和諧響應仿真分析計算。結果表明： ①軸承的剛度隨著軸承預緊力的增加而增大；②軸系的固有頻率隨著軸承預緊力的增加而增大；③主軸前段和后端的響應位移隨著軸承預緊力的增大而減少，而主軸中間的徑向響應位移隨著軸承預緊力的增大而增大。

[1]蔣書運.預緊力可控智能化高速加工電主軸[P].中國ZL200610-038219.6. 2006,10,18.

[2] [日]岡本純三，黃志強. 球軸承的設計計算[M]. 北京：機械工業出版社，2003.

[3] 劉顯軍，洪軍，朱永生，劉志剛. 多支承軸系軸承受力與剛度的有限元迭代計算方法[J]. 西安交通大學學報，2010，11.

[4] 胡愛玲. 高速電主軸動靜態特性的有限元分析[D].廣東：廣東工業大學機械工程學院，2004.

[5]劉偉，高維成，于廣濱.ANSYS12.0 寶典[M]. 北京：電子工業出版社，2010.

[6] 張珂，佟俊，吳玉厚，等. 陶瓷軸承電主軸的模態分析及其動態性能實驗[J]. 沈陽建筑大學學報（自然科學版），2008，3.

[7] Young-Kug Hwang and Choon-Man Lee. A Review on the Preload Technology of the Rolling Bearing for the Spindle of Machine Tools[J]. International Journal of Precision Engineering and Manufacturing，2010，3.

[8] Shuyun Jiang, Shufei Zheng. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics[J].International Journal of Machine Tools & Manufacture. 2010，50.