非線性系統的最小廣義Lyapunov函數定理

玉 強，吳保衛

（陜西師范大學數學與信息科學學院，西安 710062）

非線性系統的最小廣義Lyapunov函數定理

玉 強，吳保衛

（陜西師范大學數學與信息科學學院，西安 710062）

利用Zorn引理和LaSalle不變原理，研究一般非線性系統最小廣義Lyapunov函數的存在性，證明了最小（非負）廣義Lyapunov函數和最小（非負）強廣義Lyapunov函數的存在性定理.

廣義Lyapunov函數；LaSalle不變原理；Zorn引理；偏序；非線性系統

Lyapunov函數法和LaSalle不變原理［1］是研究動力系統穩定性的兩種主要工具.LaSalle不變原理不要求Lyapunov函數的正定性，且放松了Lyapunov函數導數的嚴格負定要求.因而，能處理許多Lyapunov函數方法失效的情形.LaSalle不變原理是分析自治系統和周期系統穩定性的有效工具［2－4］，但該原理不能直接應用到非線性時變系統中，因為ω－極限集可能是一個時變集［2，5］.文獻［6－15］推廣了LaSalle不變原理，使其能在更大范圍內得到應用.

但目前研究結果中，多數Lyapunov穩定性及不變集理論都要求系統的Lyapunov函數具有一階連續導數且導函數負（半）定.而由于實際系統的復雜性，如混雜系統、切換系統和生態系統等，對Lyapunov函數的可導性通常不一定能滿足［6］.另一方面，目前關于LaSalle不變原理的研究主要集中在對其使用條件及范圍的推廣，而關于如何選取及是否存在Lyapunov函數使得該函數的導數為零的區域“最接近”系統軌線的正極限集的研究報道較少.一般地，給定兩個Lyapunov函數V1和V2，稱V1“優”于V2是指使得函數V1的導數為零的區域包含于函數V2的導數為零的區域.

本文發展了（最小）廣義Lyapunov函數和（最小）強廣義Lyapunov函數等概念，這些概念不同于通常Lyapunov函數之處在于放寬了對Lyapunov函數正定性及具有一階連續導數的要求，給出了最小（非負）廣義Lyapunov函數存在性（唯一性）定理及最小（非負）強廣義Lyapunov函數存在性（唯一性）定理，從而推廣了LaSalle不變原理，且保證了“最優”廣義Lyapunov函數的存在性.

1 系統模型及引理

考慮如下非線性動力系統：

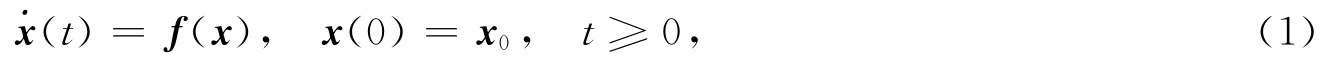
其中：x（t）∈D?Rn表示t時刻的系統狀態，D為包含0的開集；f：D→Rn為滿足Lipsitiz條件的連續函數.設系統（1）的原點是其平衡點.

若存在時間序列tn，當n→∞時，tn→∞，使得當n→∞時，x（tn）→p∈Rn，則稱p是x（t）的ω－極限點（正極限點）.x（t）所有ω－極限點構成的集合稱為x（t）的ω－極限集（正極限集）.本文用L表示x（t）的ω－極限集.

一個連續函數V（·）：D→R，若滿足對任意的t≥τ≥0，都有V（x（t））≤V（x（τ））成立，則稱V（·）為系統（1）定義在D上的廣義Lyapunov函數.令E?｛x∈D：ΔV（x（t））＝0｝，ΔV（x（t））表示“存在τ＞t，使得對任意的t′∈（t，τ），有V（x（t））＝V（x（t′））”.一般地，由LaSalle不變原理知，L?E.如果存在廣義Lyapunov函數V（x（t）），使得L＝E，則稱V（x（t））為最小廣義Lyapunov函數.

一個連續的函數V（·）：D→R，若滿足V（·）存在連續右導數，對任意的t≥0，都有D＋V（x（t））≤0成立，其中D＋V（x（t））表示V（x（t））的右導數.則稱V（·）為系統（1）定義在D上的強廣義Lyapunov函數.令E?｛x∈D：D＋V（x（t））＝0｝.如果存在強廣義Lyapunov函數V（x（t）），使得L＝E，則稱V（x（t））為最小強廣義Lyapunov函數.

引理1設g∈C1（R＋，R），其中R和R＋分別表示全體實數和非負實數構成的集合，C1（R＋，R）表示具有一階連續導數的函數g：R＋R全體.則

連續，且具有連續的右導數.

證明：先證明f（t）的連續性，分兩種情形討論.

1）若存在t1＞t≥0，使得

由g（t）的連續性知，f（t）右連續.

上述兩種情形表明，f（t）右連續.同理可證明f（t）左連續.因而f（t）連續.

下面證明f（t）右導數存在，分兩種情形討論.

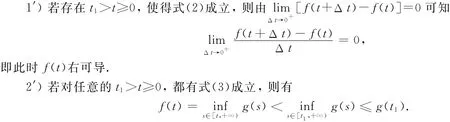
因而g（t）在t點的導數g′（t）≥0.由導函數g′（t）的連續性知，存在t2＞t，使得對任意的t′∈（t，t2），有g′（t′）＞0.若不然，設存在t3＞t，使得對任意的t′∈（t，t3），有g′（t′）≤0，則有g（t）≥g（t′），這與對任意的t′＞t都有g（t）＜g（t′）矛盾.因而，存在t2＞t，使得對任意的t′∈（t，t2）有g′（t′）＞0.

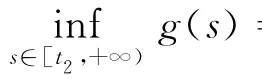
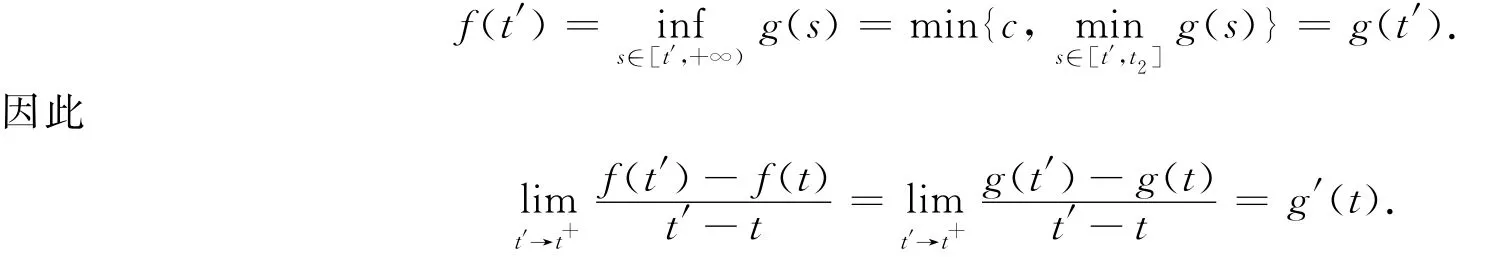
由1′），2′）知，f（t）右導數存在.

最后證明f（t）右導數的連續性.由證明f（t）右導數存在的兩種情形討論可知，f（t）右導數f′＋（t）或者為零或者等于g′（t）.無論哪種情形，都有

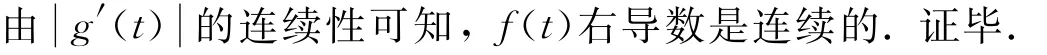
設A是一個集合，?是A上的一個嚴格偏序.若B是A的一個子集，c∈A，使得對于每個b∈B，都有b?c或c＝b，則稱c是B的一個上界.若m是A的一個元素，并且對于每個a∈A，m?a都不成立，則稱m是A的一個極大元.

類似極大元的定義，下面給出極小元的定義.設A是一個集合，?是A上的一個嚴格偏序.若B是A的一個子集，c∈A，使得對于每個b∈B，都有c?b或c＝b，則稱c是B的一個下界.若m是A的一個元素，并且對于每個a∈A，a?m都不成立，則稱m是A的一個極小元.

引理2（Zorn引理）［16］設A是一個嚴格偏序集，若A的每個全序子集都有上界，則A中必有一個極大元.

引理3設A是一個嚴格偏序集，若A的每個全序子集都有下界，則A中必有一個極小元.

證明：給定偏序集（A，?），定義新的偏序關系?′，其中?′滿足：若a，b∈A，且a?b，則b?′a.則偏序集（A，?）中的任一全序集必為偏序集（A，?′）的全序集，反之也成立.下證偏序集（A，?）中的極大元c為偏序集（A，?′）中的極小元.

設m是偏序集（A，?）的一個極大元，由極大元定義知，m∈A，且對任意的a∈A，都有m?／a.由偏序?與?′關系知，存在m∈A，且對任意的a∈A，都有a′?／m，從而m是偏序集（A，?′）的極小元.證畢.

設Λ表示系統（1）全體廣義Lyapunov函數組成的集合.對Λ進行如下分類.稱V1∈Λ與V2∈Λ同類，是指

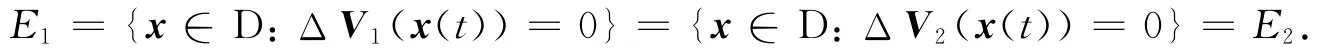
2 主要結果

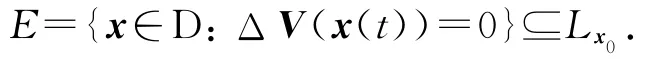
結合L x0?E和E?L x0可知，存在廣義Lyapunov函數V（x（t）），使得L x0＝E.證畢.

注1 顯然，最小廣義Lyapunov函數V（x（t））并不唯一.若用廣義Lyapunov函數等價類集合ˉΛ替換全體廣義Lyapunov函數組成的集合Λ，則可獲得最小廣義Lyapunov函數存在的唯一性定理.

注2 定理1對廣義Lyapunov函數連續性的要求可放寬到文獻［6］的下半連續.

注3 定理1表明了最小廣義Lyapunov函數的存在性，但并未給出實際構造或尋找最小廣義Lyapunov函數的方法.

可以將定理1中的結論2）加強為“對系統（1）存在非負廣義Lyapunov函數V（x（t）），使得L x0＝E＝｛x∈D：ΔV（x（t））＝0｝”.證明過程與定理1類似，只需將定理1及其證明中的“全體廣義Lyapunov函數組成的集合Λ”改為“全體非負廣義Lyapunov函數組成的集合Λ＋”，同時將1）中∈Λ＋即可.

定理2（最小非負廣義Lyapunov函數存在性定理）設Ω?D為緊集，x（t）是以x0為初態、系統（1）t時刻的狀態軌跡，且系統的解對于t＞0均停留在Ω內.L x0表示x（t）的ω－極限集，若系統（1）存在連續的正定函數V0（x（t））∈Λ＋，其中Λ＋表示全體非負廣義Lyapunov函數組成的集合.則：

1）系統原點x＝0是（Lyapunov意義下）穩定的；

2）系統（1）存在非負廣義Lyapunov函數V（x（t））∈Λ＋，使得L x0＝E＝｛x∈D：ΔV（x（t））＝0｝.

系統（1）的平衡點x＝0是半穩定的，是指平衡點x＝0為Lyapunov穩定的，且包含在平衡點x＝0某一鄰域內的系統軌線收斂到一穩定平衡點.即平衡點x＝0是Lyapunov穩定的，且包含平衡點x＝0某一鄰域內的系統軌線的ω－極限集為單點集.因而有如下推論.

推論1設Ω?D為緊集，x（t）是以x0為初態、系統（1）t時刻的狀態軌跡，且系統的解對于t＞0均停留在Ω內.L x0表示x（t）的ω－極限集，系統（1）存在連續的正定函數V0（x（t））∈Λ，且若系統（1）存在廣義Lyapunov函數V（x（t）），使得E＝｛x∈D：ΔV（x（t））＝0｝＝｛a（x0）｝為單點集，其中a：D→Rn即對確定的初始狀態x0，a（x0）為唯一確定的值，則平衡點x＝0是半穩定的.進一步，若對任意的x0∈D，有a（x0）＝0，則平衡點x＝0是漸近穩定的.

證明：由定理1結合半穩定及漸近穩定定義即可得到.由E為單點集知x（t）→a（x0），由推論1的條件知，平衡點x＝0是Lyapunov穩定的.再由半穩定定義知，平衡點x＝0是半穩定的.進一步，若對任意的x0∈D，有a（x0）＝0，則x（t）→0.因而，平衡點x＝0是漸近穩定的.證畢.

由引理1易知，定理1證明1）中選取的V u（x（t））連續，且具有連續右導數.因此，V u（x（t））為強廣義Lyapunov函數.因而，可將定理1加強為如下結論.證明過程同定理1.只需將定理1及證明中的“全體廣義Lyapunov函數組成的集合Λ”改為“全體強廣義Lyapunov函數組成的集合Γ”.

定理3（最小強廣義Lyapunov函數存在性定理）設Ω?D為緊集，x（t）是以x0為初態、系統（1）在t時刻的狀態軌跡，且系統的解對于t＞0均停留在Ω內.L x0表示x（t）的ω－極限集，若系統（1）存在連續的正定函數V0（x（t））∈Γ，則：

1）系統原點x＝0是（Lyapunov意義下）穩定的；

2）系統（1）存在強廣義Lyapunov函數V（x（t））∈Γ，使得＝E＝｛x∈D：D＋V（x（t））＝0｝.

類似于定理2的說明，將定理3的結論2）加強為“對系統（1）存在非負強廣義Lyapunov函數V（x（t）），使得L x0＝E＝｛x∈D：D＋V（x（t））＝0｝”，則有如下結果.

定理4（最小非負強廣義Lyapunov函數存在性定理）設Ω?D為緊集，x（t）是以x0為初態、系統（1）在t時刻的狀態軌跡，且系統的解對于t＞0均停留在Ω內.表示x（t）的ω－極限集，若系統（1）存在連續的正定函數V0（x（t））∈Γ＋，則：

1）系統原點x＝0是（Lyapunov意義下）穩定的；

2）系統（1）存在非負強廣義Lyapunov函數V（x（t））∈Γ＋，使得＝E＝｛x∈D：D＋V（x（t））＝0｝.其中T＋表示全體非負強廣義Lyapunov函數組成的集合.

例1考慮如下非線性系統：

［1］ LaSalle J P.Some Extensions of Liapunov’s Second Method［J］.IRE Trans Circ Theory，1960，7（4）：520－527.

［2］ Khalil H K.Nonlinear Systems［M］.NJ：Prentice Hall PTR，1996.

［3］ Hale J，LaSalle J P.Differential Equations and Dynamical Systems［M］.New York：Academic Press，1967.

［4］ Haddock J R，ZHAO Jia－xiang.Instability for Autonomous and Periodic Functional Differential Equations with Finite Delay［J］.Funkcialaj Ekvacioj，1996，39：553－570.

［5］ Sastry S.Nonlinear Systems：Analysis，Stability，and Control［M］.New York：Springer－Verlag，1999.

［6］ Chellaboina V S，Leonessa A，Haddad W M.Generalized Lyapunov and Invariant Set Theorems for Nonlinear Dynamical Systems［J］.Systems and Control Letters，1999，38（4／5）：289－295.

［7］ Byrnes C I，Martin C F.An Integral－Invariance Principle for Nonlinear Systems［J］.IEEE Transactions on Automatic Control，1995，40（6）：983－994.

［8］ Sundarapandian V.An Invariance Principle for Discrete－Time Nonlinear Systems［J］.Applied Mathematics Letters，2003，16（1）：85－91.

［9］ Chellaboina V S，Bhat S P，Haddad W M.An Invariance Principle for Nonlinear Hybrid and Impulsive Dynamical Systems［J］.Nonlinear Analysis：Theory，Methods ＆Applications，2003，53（3／4）：527－550.

［10］ WANG Jinhuan，CHENG Daizhan，HU Xiaoming.An Extension of LaSalle’s Invariance Principle for a Class of Switched Linear Systems［J］.Systems and Control Letters，2009，58（10）：754－758.

［11］ CHENG Daizhan，WANG Jinhuan，HU Xiaoming.An Extension of LaSalle’s Invariance Principle and Its Application to Multi－agent Consensus［J］.IEEE Transactions on Automatic Control，2008，53（7）：1765－1770.

［12］ Mancilla－Aguilar J L，Garcia R A.An Extension of LaSalle’s Invariance Principle for Switched Systems［J］.Systems and Control Letters，2006，55（5）：376－384.

［13］ Valentino M C，Oliveira V A，Alberto L F C，et al.An Extension of the Invariance Principle for Dwell－Time Switched Systems［J］.Systems and Control Letters，2012，61（4）：580－586.

［14］ Bonotto E M.LaSalle’s Theorems in Impulsive Semidynamical Systems［J］.Nonlinear Analysis：Theory，Methods ＆Applications，2009，71（5／6）：2291－2297.

［15］ Ignatyev A O，Ignatyev O A.Stability Investigation of Invariant Sets by Means of Semidefinite Lyapunov Functions［J］.Nonlinear Analysis：Real World Applications，2011，12（3）：1453－1458.

［16］ James R M.Topology［M］.New Jersey：Prentice Hall Inc，1975.

Minimal Generalized Lyapunov Function Theorems for Nonlinear Systems

YU Qiang，WU Baowei
（CollegeofMathematicsandInformationScience，ShaanxiNormalUniversity，Xi’an710062，China）

Based on Zorn’s lemma and LaSalle’s invariance principle，the existence of the minimal generalized Lyapunov function for nonlinear systems was considered.We developed the minimal generalized Lyapunov function theorems and the minimal strong generalized Lyapunov function theorems for nonlinear dynamical systems.

generalized Lyapunov function；LaSalle’s invariance principle；Zorn’s lemma；partial order；nonlinear system

O231.2

A

1671－5489（2014）03－0445－06

10.13413／j.cnki.jdxblxb.2014.03.08

2013－06－26.

玉 強（1979—），男，漢族，博士研究生，從事非線性分析及穩定性的研究，E－mail：yuqiang111111＠126.com.通信作者：吳保衛（1963—），男，漢族，博士，教授，從事控制理論及線性系統的研究，E－mail：wubw＠snnu.edu.cn.

國家自然科學基金（批準號：11171197）.

趙立芹）