半線性隨機變延遲微分方程數值解的收斂性

劉國清，張 玲

（大慶師范學院數學科學學院，黑龍江大慶 163712）

半線性隨機變延遲微分方程數值解的收斂性

劉國清，張 玲

（大慶師范學院數學科學學院，黑龍江大慶 163712）

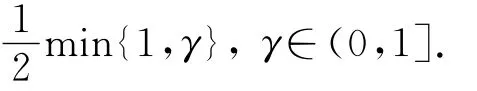
隨機變延遲微分方程；指數Euler方法；Lipschitz條件；It?公式；強收斂性

隨機模型在生物學、傳染病、經濟與金融等領域應用廣泛.大多數隨機微分方程都是非線性的，其解析解不能表達為顯式形式，因此，數值解的研究在實際應用中非常重要.隨機微分方程數值解的研究目前已有許多成果［1－5］，Higham等［3］給出了隨機微分方程數值解的幾乎處處與矩指數穩定性.文獻［6－11］研究了隨機延遲微分方程.曹婉蓉等［6］給出了隨機延遲微分方程Euler－Maruyama方法的均方穩定性；毛學榮［11］討論了隨機延遲微分方程Euler－Maruyama方法的指數穩定性.對于半線性隨機延遲微分方程指數Euler方法的收斂性和穩定性研究目前報道較少.文獻［6－7］首先把指數Euler方法應用到隨機微分方程上；文獻［12］給出了隨機微分方程指數Euler方法的穩定性和收斂性；文獻［13］應用Lyapunov方法給出了常延遲隨機微分方程指數Euler方法的收斂性和穩定性；文獻［14］用直接證明方法給出了兩類隨機延遲微分方程指數Euler方法的收斂性和指數穩定性.本文給出該隨機變延遲微分方程的指數Euler方法，得到了其數值解的收斂性.

1 預備知識及指數Euler方法

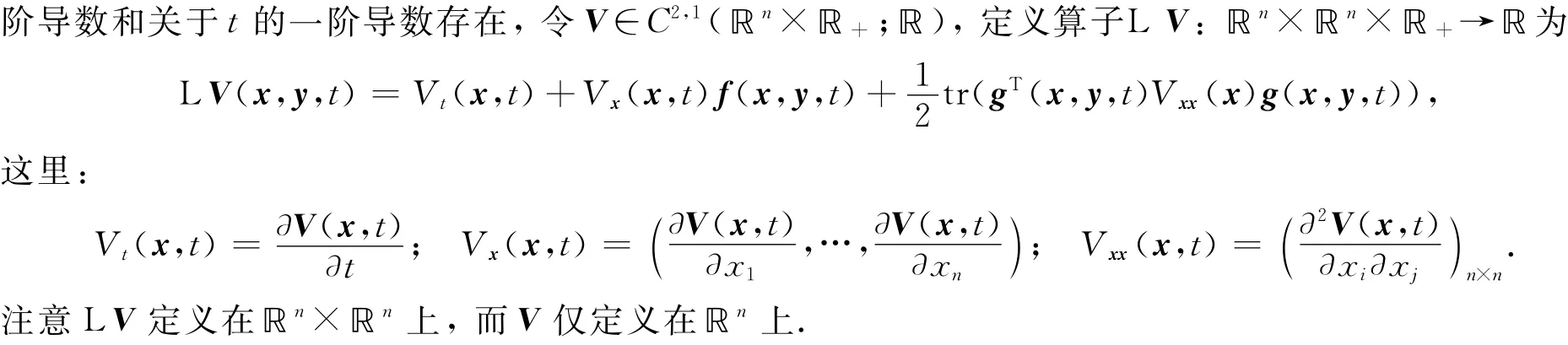
2 指數Euler方法數值解的收斂性

引理1如果線性增長條件（H2）成立，則存在常數C1＞0，使得方程（1）的精確解和連續指數Euler方法的近似解（5）滿足如下關系：

3 數值算例

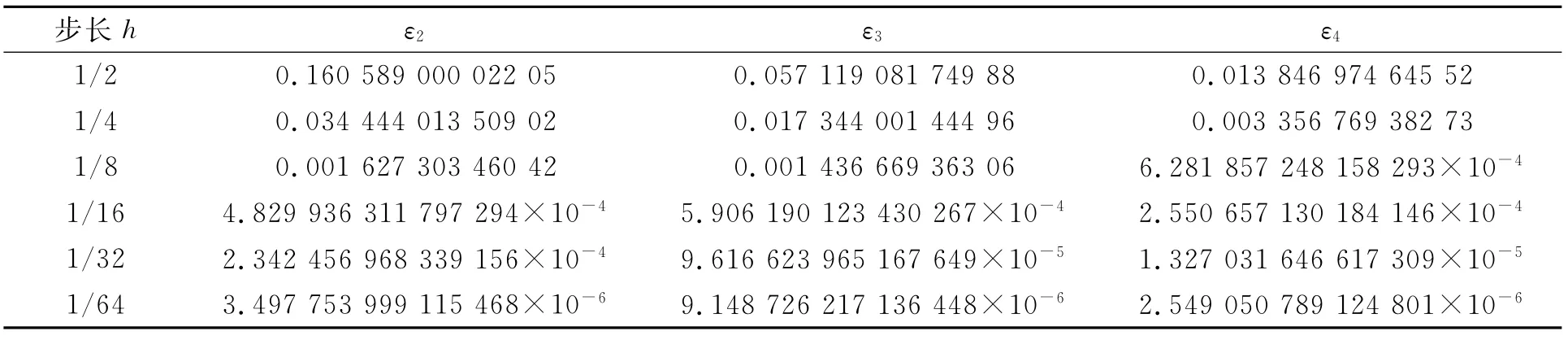
表1 指數Euler方法數值解的全局誤差Table 1 Global error of numerrical solutions by the exponential Euler method

［1］ Friedman A.Stochastic Differential Equations and Applications［M］.New York：Academic Press，1975.

［2］ Higham D J.An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations［J］.SIAM Review，2001，43（3）：525－546.

［3］ Higham D J，MAO Xuerong，YUAN Chenggui.Almost Sure and Moment Exponential Stability in the Numerical Simulation of Stochastic Differential Equations［J］.SIAM J Numer Anal，2007，45（2）：592－609.

［4］ MAO Xuerong.Stochatic Differential Equations and Applications［M］.Chichester：Horwood Publishing，1997.

［5］ MAO Xuerong，YUAN Chenggui.Stochastic Differential Equations with Markovian Switching［M］.London：Imperial College Press，2006.

［6］ CAO Wanrong，LIU Mingzhu，FAN Zhencheng.MS－Stability of the Euler－Maruyama Method for Stochastic Differential Delay Equations［J］.Appl Math Comput，2004，159（1）：127－135.

［7］ 范振成，劉明珠.隨機延遲微分方程數值解的p階均方指數穩定［J］.黑龍江大學自然科學學報，2005，22（4）：468－470.（FAN Zhencheng，LIU Mingzhu.Thepth Moment Exponential Stability for the Stochastic Delay Differential Equation［J］.Journal of Natural Science of Heilongjiang University，2005，22（4）：468－470.）

［8］ MAO Xuerong.Numerical Solutions of Stochastic Differential Delay Equations under the Generalized Khasminskii－Type Conditions［J］.App Math Comput，2011，217（12）：5512－5524.

［9］ MAO Xuerong.Numerical Solutions of Stochastic Functional Differential Equations［J］.LMS J Comput Math，2003，6：141－161.

［10］ MAO Xuerong，Sabanis S.Numerical Solutions of Stochastic Differential Delay Equations under Local Lipschitz Condition［J］.J Comput Appl Math，2003，151（1）：215－227.

［11］ MAO Xuerong.Exponential Stability of Equidistant Euler－Maruyama Approximations of Stochastic Differential Delay Equations［J］.J Comput Appl Math，2007，200（1）：297－316.

［12］ 史春妹.隨機微分方程指數Euler方法收斂性和穩定性［D］.哈爾濱：哈爾濱工業大學，2011.（SHI Chunmei.The Convergence and Stability of Exponential Euler Method for Stochastic Differential Equations［D］.Harbin：Harbin Institute of Technology，2011.）

［13］ 周雪.隨機延遲微分方程指數Euler法的收斂性和穩定性［D］.哈爾濱：哈爾濱工業大學，2012.（ZHOU Xue.Convergence and Stability of Exponential Euler Method for Stochastic Delay Differential Equations［D］.Harbin：Harbin Institute of Technology，2012.）

［14］ 張玲.幾類隨機延遲微分方程的數值分析［D］.哈爾濱：哈爾濱工業大學，2013.（ZHANG Ling.Numerical Analysis for Several Classes of Stochastic Delay Differential Equations［D］.Harbin：Harbin Institute of Technology，2013.）

Convergence of Numerical Solutions for Semi－linear Stochastic Variable Delay Differential Equations

LIU Guoqing，ZHANG Ling
（SchoolofMathematicalSciences，DaqingNormalUniversity，Daqing163712，HeilongjiangProvince，China）

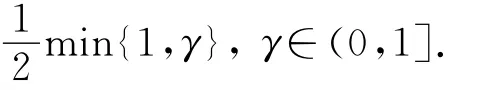
stochastic variable delay differential equation；exponential Euler method；Lipschitz condition；It?formula；strong convergence

O241.81

A

1671－5489（2014）03－0451－09

10.13413／j.cnki.jdxblxb.2014.03.09

2013－11－22.

劉國清（1966—），男，漢族，碩士，教授，從事拓撲動力系統的研究，E－mail：lgq660609＠163.com.通信作者：張 玲（1978—），女，漢族，博士，講師，從事微分方程數值解和隨機過程的研究，E－mail：zl78521＠163.com.

黑龍江省教育廳科研項目（批準號：11553003）.

趙立芹）