基于魯棒迭代優化的圖像拼接算法*
杜培明 ,邢 碩 ,2
(1.安徽工業大學電氣信息學院,安徽 馬鞍山 243032;2.銅陵學院電氣工程學院,安徽 銅陵 244061)
基于魯棒迭代優化的圖像拼接算法*
杜培明1,邢 碩1,2
(1.安徽工業大學電氣信息學院,安徽 馬鞍山 243032;2.銅陵學院電氣工程學院,安徽 銅陵 244061)
針對保持直線邊緣不畸變和改善拼接區域精度的需要,提出了一種基于魯棒迭代優化的圖像拼接算法。采用SIFT特征匹配算法提取不變特征,依據RANSAC魯棒算法估計單應性矩陣獲取精確內點匹配點對,參照內點匹配點對作為參數,利用最小二乘法重新估計單應性矩陣,最終通過魯棒迭代優化重新計算更多內點直至內點收斂。實驗結果表明,所提出的算法使得直線邊緣維持直線化,同時拼接精度得到提高。
SIFT特征匹配;RANSAC魯棒估計;最小二乘估計;迭代優化
1 引言
圖像拼接技術是依賴采集的重疊圖像集合,利用計算機視覺進行圖像間的相互匹配,并將其拼接成無縫高分辨率圖像的過程。其本質是獲取最優坐標空間映射的單應性矩陣,對待拼接圖像進行空間幾何變換,使得位于不同視點下的圖像公共區域相互匹配,實現圖像公共區域相互重疊和非公共區域相互拼接。現今,圖像拼接技術已經成為計算機視覺的研究熱點,并被廣泛應用到遙感圖像處理、醫學圖像處理、超分辨率圖像重構等領域。
圖像匹配是指通過匹配算法識別兩幅或多幅圖像間的同名點,其是實現圖像拼接的關鍵和核心,可劃分為區域匹配[1,2]和特征匹配[3~5]。區域匹配利用區域統計量的相似性度量來實現圖像匹配,但其不能實現校正圖像形變,且域搜索的運算量較大,特征匹配利用提取不變性特征來估計圖像匹配,其依據不變性特征間的匹配關系來建立圖像間的映射關系,因而大大減少了算法的復雜度,但其關鍵在于如何有效提高匹配質量。
特征匹配是指通過提取圖像的特征和對特征進行參數描述,再運用描述參數來進行匹配的過程。文獻[3]提出了依據不變特征實現全景圖像自動拼接,而對于近景圖像拼接直線部分會產生曲線化;文獻[4,5]針對空間變換簡單的眼底圖像進行圖像拼接,圖像不存在大幅度的旋轉變換和尺度變換,僅依據MLESAC算法進行剔除,難以得到精度較高的圖像拼接;文獻[6]給出了利用圓柱拼接算法來實現的柱面全景圖拼接,然而柱面拼接會導致圖像發生畸變,使得圖像中的直線變化為曲線,不適用于矩形度檢測等場合。
鑒于圖像拼接保持直線化和提高精度的需要,本文提出了一種基于魯棒迭代優化的圖像拼接算法。通 過 SIFT(Scale-Invariant Feature Transform)特征匹配算法提取初始匹配點對,依據RANSAC(Random Sample Consensus)算法估計單應性矩陣獲取內點,用以剔除匹配過程中的誤匹配點對,再參照內點利用最小二乘法來重新估計單應性矩陣,采用迭代優化重新計算內點,重復循環直至內點數目收斂,從而最終獲取圖像拼接的映射關系。
2 SIFT特征匹配
在采集拼接圖像過程中,圖像存在旋轉變換和尺度變換,使得傳統信息匹配和角點匹配難于適用,而 SIFT 特征提取[7,8]具有光照、尺度、旋轉不變性,且穩定性較好,從而適用于拼接圖像的旋轉變化和尺度變化。
SIFT算法主要包含以下步驟:(1)建立DoG尺度空間,搜索該空間下的極值;(2)依據DoG空間極值,精確定位其位置和尺度;(3)計算關鍵點梯度直方圖,確定其主方向;(4)利用梯度直方圖,生成特征描述子。
SIFT特征提取完成后,需要依賴特征描述確定匹配點對。通常采用特征描述的歐氏距離作為相似性度量,取基準圖像的某個SIFT基準點,利用kd-樹在待匹配圖像中搜索最近鄰和次近代匹配點,若最近距離除以次近距離小于某個閾值,則接受該匹配點對。
3 射影變換
射影變換[9]描述著空間坐標點在不同坐標系下的投影映射關系,設基準圖像中點x和待匹配圖像中點x′為同一空間坐標點,則存在單應性矩陣H 滿足式(1):
矢量x′和矢量Hx相互平行,則有式(2):

基準圖像的基準點到待匹配圖像的映射關系如式(3)所示:
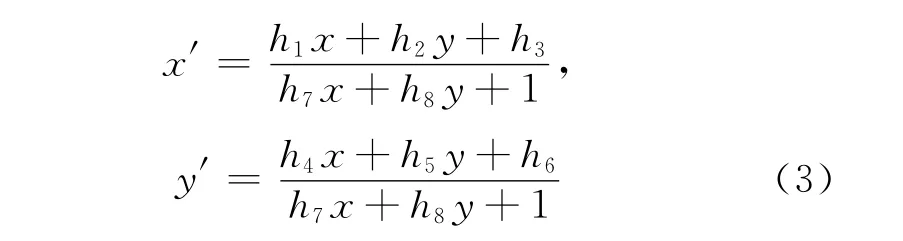
單應性矩陣H的自由度為8,則有:

其中,h為H的前八個元素組成的八維矢量,i=1,…,4。
4 圖像拼接
4.1 RANSAC魯棒估計
設經SIFT特征匹配獲取的匹配點對數目為N,匹配點對為xi和,則依據代價函數Jr值最優來估計單應性矩陣H,如式(5)所示:
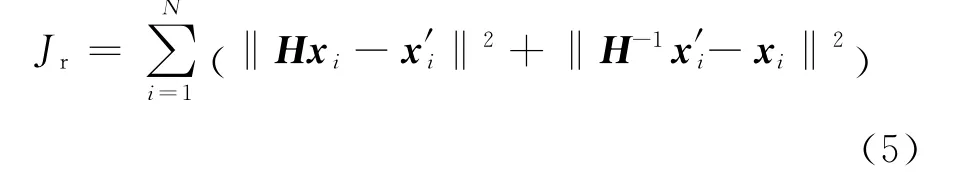
RANSAC魯棒估計[9]步驟如下:
(1)隨機從N對SIFT特征匹配點對中選取四對匹配點對,并以此作為參數依據式(4)求取單應性矩陣H。
(2)利用單應性矩陣H將N 對匹配點對xi和分別映射到對方空間中,依據式(5)計算代價函數Jr值。
(3)修正循環變量Count,當Count為正時,重復(1)~ (3)。其中,Count=log(1-p)/log(1-(1-ε)s),p=0.99,1-ε表示內點概率,ε表示野值概率。
(4)選取代價函數Jr值最小的單應性矩陣H作為RANSAC映射矩陣Hr,并由式(6)和式(7)依據歐氏距離dist判別xi和為內點或野值,其中內點數目為M,則野值數目為N-M。
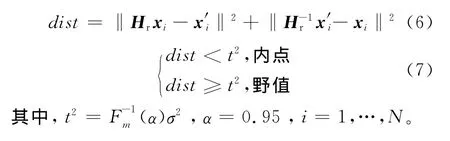
4.2 最小二乘估計
經RANSAC算法獲取的單應性矩陣Hr,僅由4個匹配點對其進行描述,使其精度難以達到可靠保證,在此希望依據RANSAC算法獲取的內點,利用最小二乘法來重新估計LS映射矩陣Hl。
依據式(4)變換可得式(8):
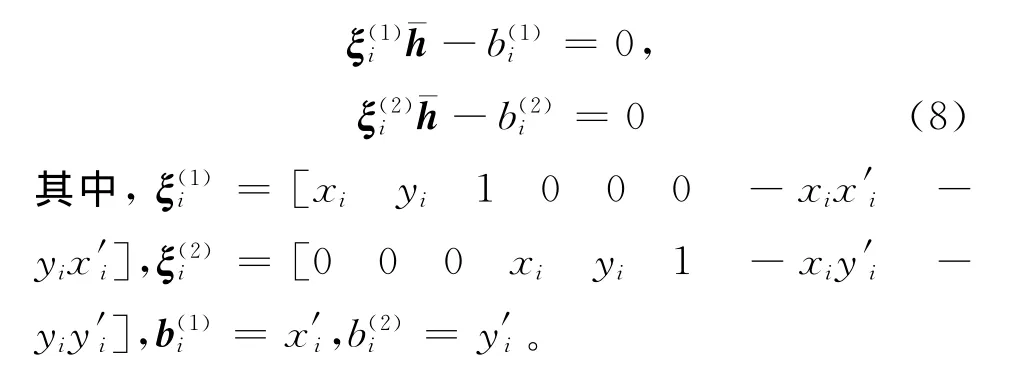
依據M個內點對應的代價函數Jl值最優來增強估計單應性矩陣Hl,如式(9)和式(10)所示。
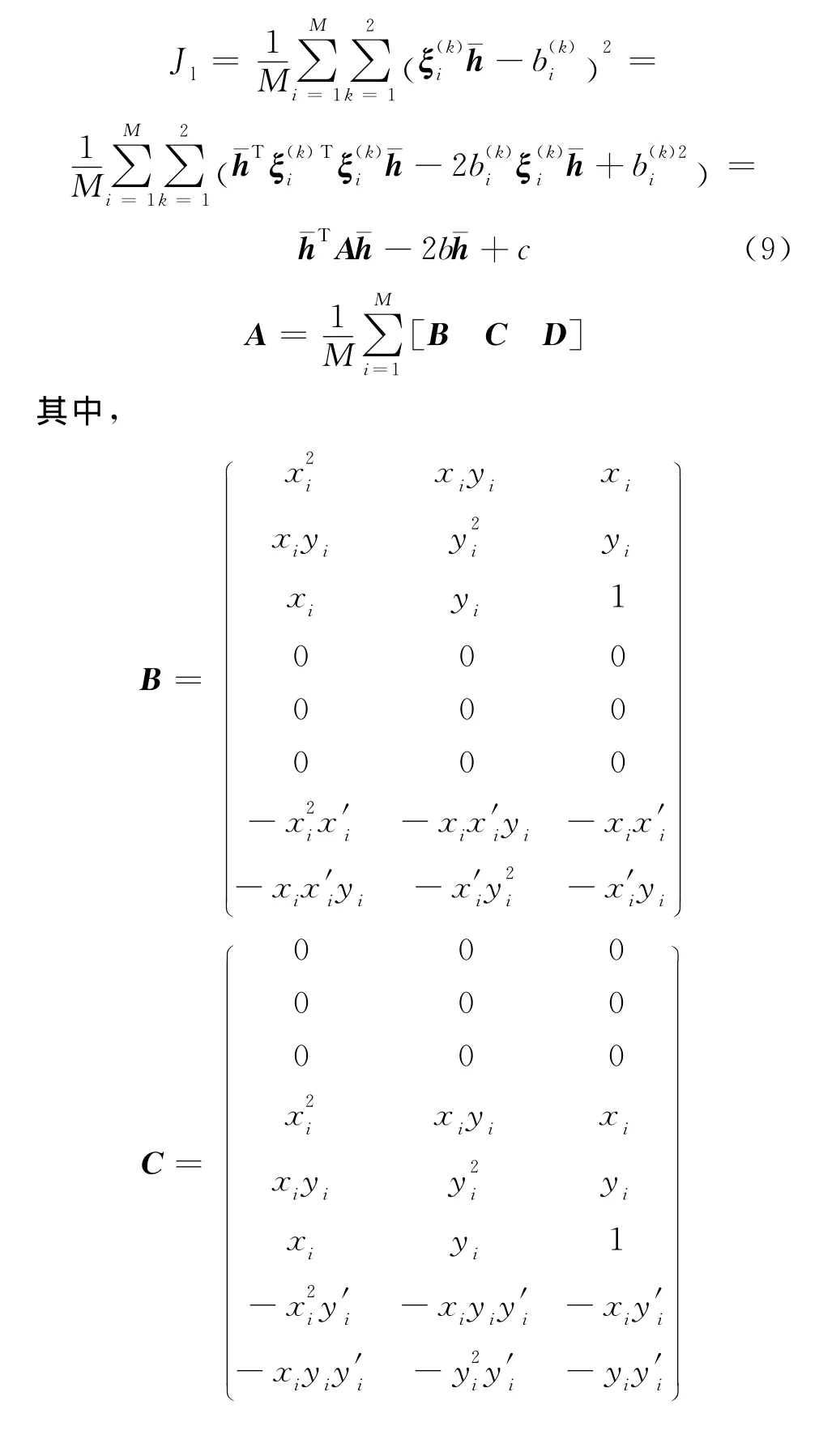

4.3 魯棒迭代優化
經最小二乘估計獲取的單應性矩陣Hl,在此希望獲取更多的內點使得估計精度更高,考慮利用單應性矩陣Hl重新計算內點數目,并重復該循環直至內點數目收斂。
魯棒迭代優化步驟如下:
(1)依據RANSAC魯棒估計獲取RANSAC映 射矩陣,并據此計算內點數目M(0);
(2)依賴 M(i-1)內點坐標利用最小二乘估計獲取LS映射矩陣,并據此重新計算內點數目M(i);
(3)判別 M(i)>,若該式成立,重復(2)~(3),否則結束循環,并以作為最終的單應性矩陣。
5 實驗結果與分析
5.1 近距場景
近距場景圖像包含旋轉變換和尺度變換,以幾本相互平行的書置于實驗臺上,離攝像機鏡頭較遠的書變形較強,如圖1a和圖1b所示,以書和實驗臺的邊緣保持線形為要求,進而依據本文算法實現圖像拼接。
近距場景圖像經由SIFT特征匹配,獲取97對初始匹配點對,如圖1c所示;通過RANSAC魯棒估計,獲取62對內點匹配點對,如圖1d所示;經過最小二乘估計,獲取LS映射矩陣進行圖像拼接,如圖1e所示;經過三次迭代優化,獲取74對內點匹配點對,獲取LS映射矩陣進行圖像拼接,如圖1f所示。

Figure 1 Close shot experiment圖1 近距場景實驗
從實驗結果可以看出,圖1a經單應性變換后,書與實驗臺能較好地保持直線不畸變,書矩形度恢復情況表現較好,同時拼接交界處能夠實現無縫拼接,隨著迭代次數增加,內點數目逐步增加,拼接效果逐步增強,如圖1e、圖1f和圖2所示。

Figure 3 Distant view experiment圖3 遠距場景實驗

Figure 2 Relation of inner points number and iterations圖2 內點數目與迭代次數變化關系
5.2 遠距場景
遠距場景圖像包含旋轉變換和尺度變換,包含遠處建筑、湖面和山體,離攝像機鏡頭較遠場景幾何變換較為簡單,如圖3a所示。
遠距場景的實驗過程與近距場景基本一致,依據各幅圖像的匹配區域進行拼接,此處以第二幅圖像為拼接中心,其他圖像參照第二幅圖像進行拼接。從實驗結果可以看出,距離拼接中心較近的圖像在拼接過程中變形相對較小,各幅圖像基本實現無縫拼接,整合為一幅高分辨率圖像。
6 結束語
本文應用魯棒迭代優化方法對存在旋轉和尺度變換的圖像進行拼接,采用SIFT特征匹配算法提取匹配點對;依賴RANSAC魯棒算法估計單應性矩陣;并據此獲取精確內點匹配點對,依照內點匹配點對作為參數,利用最小二乘法重新估計單應性矩陣,再依據魯棒迭代優化重新計算更多內點直至內點收斂。實驗結果表明,在近距場景和遠距場景圖像拼接過程中,本文方法均能得到較為滿意的拼接結果。
[1] Wolberg G,Zokai S.Robust image registration using log-polar transform[C]∥Proc of IEEE International Conference on Image Processing,2000:493-496.
[2] Viola P,Willian M.Alignment by maximization of mutual information[J].International Journal of Computer Vision,1997,24(2):137-154.
[3] Brown M,Lowe D G.Automatic panoramic image stitching using invariant features[J].International Journal of Computer Vision,2007,74(1):59-73.
[4] Wang Yu-liang,Shen Jian-xin,Liao Wen-he,et al.Automatic fundus images mosaic based on SIFT feature[C]∥Proc of the 3rd International Congress on Image and Processing,2011:2747-2751.
[5] Wang Yu-liang,Shen Jian-xin,Liao Wen-he.Automatic fundus images registration and mosaic based on SIFT feature[J].Journal of Nanjing University of Aeronautics & Astro-nautics,2011,43(2):222-228.(in Chinese)
[6] Shum H,Szeliski R.Panoramic image mosaics[R].Redmond:Microsoft Research,2001:1-50.
[7] Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[8] Beis J S,Lowe D G.Shape indexing using approximate nearest-neighbour search in high-dimensional spaces[C]∥Proc of IEEE 1997Computer Society Conference on Computer Vision and Pattern Recognition,1997:1000-1006.
[9] Hartley R,Zisserman A.Multiple view geometry in computer vision[M].UK:Cambridge University Press,2000.
附中文參考文獻:
[5] 王玉亮,沈建新,廖文和.基于尺度不變特征的眼底圖像自動配準與拼接[J].南京航空航天大學學報,2011,43(2):222-228.
Image mosaic based on robust iterative optimization
DU Pei-ming1,XING Shuo1,2
(1.School of Electrical Engineering &Information,Anhui University of Technology,Ma’anshan 243032;2.School of Electrical Engineering,Tongling University,Tongling 244061,China)
Aiming at the requirements of keeping edges in a straight line and improving the mosaic precision,an image mosaic algorithm based on robust iterative optimization is proposed.Firstly,SIFT feature matching algorithm is employed to extract features with invariance.Secondly,inlier matching points are obtained accurately through the homography matrix that is estimated according to RANSAC robust algorithm.Thirdly,the homography matrix is re-estimated utilizing least square method by treating inliers as parameters.Finally,more inliers are recomputed until converge based on robust iterative optimization.Experimental results show that,with the proposed method,edges are maintained as a straight line and the precision of image mosaic is greatly improved.
SIFT feature matching;RANSAC robust estimation;least-squares estimation;iterative optimization
TP391.41
A
10.3969/j.issn.1007-130X.2014.04.029
2012-10-24;
2013-01-21
通訊地址:244061安徽省銅陵市銅陵學院電氣工程學院
Address:School of Electrical Engineering,Tongling University,Tongling 244061,Anhui,P.R.China
1007-130X(2014)04-0741-05
杜培明(1964-),男,安徽馬鞍山人,副教授,研究方向為圖像處理。E-mail:dpm1717@ahut.edu.cn
DU Pei-ming,born in 1964,associate professor,his research interest includes image processing.

