遵循“兩個(gè)尊重” 提高數(shù)學(xué)作業(yè)講評(píng)有效性

☉浙江省義烏市第二中學(xué) 龔輝斌

遵循“兩個(gè)尊重” 提高數(shù)學(xué)作業(yè)講評(píng)有效性

☉浙江省義烏市第二中學(xué) 龔輝斌

作為數(shù)學(xué)日常教學(xué)的重要組成部分，作業(yè)講評(píng)在促進(jìn)學(xué)生對(duì)于數(shù)學(xué)知識(shí)的理解、數(shù)學(xué)技能和方法的掌握、加速數(shù)學(xué)思想的領(lǐng)悟等方面具有重要的意義.然而，我們發(fā)現(xiàn)，作業(yè)講評(píng)教學(xué)普遍存在以下問(wèn)題：缺乏以學(xué)生作業(yè)的實(shí)際解答情況為講評(píng)出發(fā)點(diǎn)的意識(shí)，導(dǎo)致講評(píng)的針對(duì)性不強(qiáng)；目標(biāo)局限于單純的“糾錯(cuò)”和“解惑”，導(dǎo)致講評(píng)的育人功能缺失……“數(shù)學(xué)是思維的科學(xué).”［1］數(shù)學(xué)作業(yè)講評(píng)是思維活動(dòng)的講評(píng).上述問(wèn)題的存在，不利于激發(fā)和維持學(xué)生數(shù)學(xué)學(xué)習(xí)的熱情，不利于學(xué)生思維能力的和諧健康發(fā)展.為實(shí)現(xiàn)數(shù)學(xué)作業(yè)講評(píng)的有效性，筆者以為遵循“兩個(gè)尊重”至關(guān)重要.

一、“兩個(gè)尊重”的涵義

1.尊重學(xué)生的思維

尊重學(xué)生的思維，包括兩個(gè)方面：一是尊重由作業(yè)反映的學(xué)生的思維特點(diǎn)和思維規(guī)律.這就是說(shuō)，既要積極評(píng)價(jià)學(xué)生作業(yè)中有效的、高品質(zhì)的數(shù)學(xué)思維活動(dòng)，又要認(rèn)真分析可能存在的思維缺陷、不足和錯(cuò)誤，這是作業(yè)講評(píng)不可或缺的環(huán)節(jié)；二是尊重學(xué)生伴隨講評(píng)教學(xué)的思維發(fā)展權(quán).作業(yè)講評(píng)的根本目的是發(fā)展學(xué)生的思維能力.講評(píng)教學(xué)并非單向的思維灌輸過(guò)程，而是在教師引領(lǐng)下學(xué)生對(duì)作業(yè)題再思考、對(duì)原解答再審視的過(guò)程，因而學(xué)生的思維活動(dòng)占據(jù)了講評(píng)活動(dòng)的重要成分，教師的“教”是為改進(jìn)學(xué)生的解答、提升學(xué)生的思維品質(zhì)服務(wù)的.總的來(lái)說(shuō)，尊重學(xué)生的思維，要求我們既重視學(xué)生“作業(yè)中的思維”，又重視學(xué)生“課堂上的思維”，兩者互為聯(lián)系，并行不悖.

2.尊重?cái)?shù)學(xué)的思維

尊重?cái)?shù)學(xué)的思維，就是以具有普遍意義的、宏觀的數(shù)學(xué)思維方式作為作業(yè)講評(píng)的主旋律，以此引領(lǐng)學(xué)生糾正思維錯(cuò)誤、彌補(bǔ)思維缺陷、開拓思維空間，幫助學(xué)生養(yǎng)成科學(xué)有效的思考習(xí)慣，形成對(duì)數(shù)學(xué)完整和深刻的認(rèn)識(shí).

尊重?cái)?shù)學(xué)的思維，是追求作業(yè)講評(píng)的高品位、強(qiáng)化思想性教學(xué)的必然要求.囿于就題論題的作業(yè)講評(píng)有可能導(dǎo)致學(xué)生思維的低層次徘徊.尊重?cái)?shù)學(xué)的思維，就是以數(shù)學(xué)中思考問(wèn)題、分析問(wèn)題的一般方法引導(dǎo)學(xué)生的思維再起步，以高影響力的策略性知識(shí)促使學(xué)生思維的升華，克服常見的“只見步驟，不見思想”的傾向，從根本上提升作業(yè)講評(píng)的境界，為學(xué)生謀取長(zhǎng)遠(yuǎn)的發(fā)展利益.

二、“兩個(gè)尊重”的落實(shí)

“兩個(gè)尊重”落實(shí)于具體的課堂教學(xué)，需要我們切實(shí)處理好數(shù)學(xué)方面和教育方面的關(guān)系，數(shù)學(xué)方面做到“內(nèi)容深刻、到位”，教育方面做到“形式科學(xué)、高效”.

1.作業(yè)批改環(huán)節(jié)了解學(xué)生思維中的突出問(wèn)題，講評(píng)伊始展示有典型意義的作業(yè)解答

作業(yè)講評(píng)，與其說(shuō)講教師所知道的，倒不如說(shuō)講學(xué)生正需要的.學(xué)生的作業(yè)解答為教師了解學(xué)生的數(shù)學(xué)學(xué)習(xí)狀況提供了最全面、最深刻的材料.在作業(yè)批改環(huán)節(jié)，從尊重學(xué)生的思維出發(fā)，把了解學(xué)生的思維狀況放在突出的位置是講評(píng)教學(xué)有的放矢、實(shí)現(xiàn)高效優(yōu)質(zhì)的前提.為此，教師需要有“透過(guò)現(xiàn)象看本質(zhì)”的意識(shí)和能力.這就是說(shuō)，我們不僅要看到學(xué)生作業(yè)中的顯性表現(xiàn)，更要窺探其背后的思維過(guò)程，并對(duì)其思維品質(zhì)作出恰當(dāng)?shù)脑u(píng)價(jià).講評(píng)課上常見的“滿堂灌”、“無(wú)病呻吟”和“啟而不發(fā)”等不良現(xiàn)象，本質(zhì)上與教師課前了解作業(yè)反映的學(xué)生思維現(xiàn)狀不夠密切相關(guān).

尊重學(xué)生的思維，需要讓學(xué)生個(gè)體感受到老師對(duì)其思維活動(dòng)的關(guān)注.具體地說(shuō)，作業(yè)批改時(shí)，發(fā)現(xiàn)了學(xué)生作業(yè)中的思維閃光點(diǎn)，教師應(yīng)該及時(shí)用文字或符號(hào)給予熱情的評(píng)價(jià)，同時(shí)做好摘錄，以便在后來(lái)的課堂講評(píng)時(shí)與全班同學(xué)共享，并“發(fā)揚(yáng)光大”；而對(duì)于學(xué)生思維中存在的問(wèn)題，教師不應(yīng)該簡(jiǎn)單地以“錯(cuò)”、“壞”評(píng)價(jià)之，而應(yīng)該作出具體的分析.比如，作業(yè)中的一些錯(cuò)誤表面上看與學(xué)生對(duì)知識(shí)的理解、技能的掌握有關(guān)，可能根本的原因還是不良的思維品質(zhì)和習(xí)慣，為此，教師作出簡(jiǎn)短的點(diǎn)評(píng)和提示是必要的.

2.把數(shù)學(xué)概念的內(nèi)涵、數(shù)學(xué)方法的作用和數(shù)學(xué)思想的本質(zhì)等作為講評(píng)的核心內(nèi)容，以此占據(jù)講評(píng)教學(xué)的制高點(diǎn)

“有些題目的難度是由題目本身和所用的數(shù)學(xué)方法決定的，倘若不從數(shù)學(xué)方法上下功夫，僅僅從教學(xué)方法的角度出發(fā)，學(xué)生學(xué)習(xí)起來(lái)仍然很辛苦.”［2］尊重?cái)?shù)學(xué)的思維，要求教師圍繞學(xué)生的作業(yè)表現(xiàn)，以數(shù)學(xué)概念、方法和思想為載體，不僅把其中的思維講清楚，更要講深刻.史寧中先生指出，“一個(gè)學(xué)者或發(fā)明家得到的最后結(jié)論可能是非常完美，但頭腦中思考的是非常簡(jiǎn)潔的東西.”［3］高層次的作業(yè)講評(píng)就是要讓學(xué)生學(xué)會(huì)像學(xué)者和發(fā)明家那樣簡(jiǎn)潔地思維.

3.平衡“學(xué)”和“教”兩個(gè)方面的作用，追求作業(yè)講評(píng)效益最大化

遵循“兩個(gè)尊重”，要求我們緊緊圍繞“糾錯(cuò)和解惑”這一短期目標(biāo)和“發(fā)展學(xué)生的認(rèn)識(shí)力和思維力”這一長(zhǎng)期目標(biāo)，積極處理好學(xué)生的主體性和教師的主導(dǎo)性關(guān)系.

具體地說(shuō)，一方面，作業(yè)講評(píng)要自始至終強(qiáng)調(diào)學(xué)生思維的實(shí)質(zhì)性參與，強(qiáng)化學(xué)生的思維體驗(yàn).實(shí)踐證明，學(xué)生糾正作業(yè)中的錯(cuò)誤、克服作業(yè)中的困難并不能單純依靠他人的講授，而主要是一個(gè)思維引領(lǐng)和行為操作相結(jié)合的自我否定、自我發(fā)展的過(guò)程.事實(shí)上，不經(jīng)過(guò)思考的不是數(shù)學(xué)，作業(yè)講評(píng)給予了學(xué)生再學(xué)習(xí)再創(chuàng)造的機(jī)會(huì).

另一方面，作業(yè)講評(píng)要充分發(fā)揮教師對(duì)數(shù)學(xué)理解深刻的優(yōu)勢(shì)，強(qiáng)化示范和引領(lǐng)作用.數(shù)學(xué)問(wèn)題的復(fù)雜性、數(shù)學(xué)思維的抽象性和學(xué)生智力的局限性決定了單純依靠學(xué)生自己的努力往往很難取得根本性的糾錯(cuò)和問(wèn)題關(guān)鍵處的突破.教師必須抓住時(shí)機(jī)，理直氣壯、毫不含糊地以自己的理解力培養(yǎng)學(xué)生的理解力，以自己的思維力發(fā)展學(xué)生的思維力，體現(xiàn)教師的實(shí)質(zhì)性作用.例如，學(xué)生作業(yè)中的錯(cuò)誤和困難常常源于數(shù)學(xué)的形式化特征.形式化的表達(dá)具有簡(jiǎn)潔、深刻的特點(diǎn)，是一種文化繼承行為.然而，數(shù)學(xué)的形式化遠(yuǎn)離了學(xué)生的原有經(jīng)驗(yàn)和生活實(shí)際，自然會(huì)給學(xué)生的理解和運(yùn)用帶來(lái)困惑，造成學(xué)生作業(yè)中這樣那樣的錯(cuò)誤和困難.如果教師不采取針對(duì)性的主導(dǎo)措施，學(xué)生可能永遠(yuǎn)也明白不了問(wèn)題的本質(zhì)，走不出迷霧.

三、案例：一道“解含參不等式”作業(yè)的講評(píng)

學(xué)完了人教A版必修5第三章“不等式”，筆者在一次綜合練習(xí)中布置了下面的作業(yè)題

通過(guò)批改，發(fā)現(xiàn)了2種有代表性的（不正確）解答.講評(píng)伊始，利用投影儀，這2種解答展示如下：

課堂活動(dòng)片段之一：用數(shù)學(xué)概念引領(lǐng)思維活動(dòng)

師：解答1存在什么問(wèn)題嗎？

教室很安靜，看來(lái)學(xué)生處于困惑之中.

師：請(qǐng)大家看一看它的推理過(guò)程.推理有問(wèn)題嗎？

學(xué)生一致認(rèn)為推理沒(méi)有錯(cuò)誤.

師：既然推理沒(méi)有錯(cuò)誤，看來(lái)問(wèn)題出在解題目標(biāo)的實(shí)現(xiàn)上.誰(shuí)來(lái)說(shuō)一說(shuō)，“解不等式”的含義是什么？

課堂上請(qǐng)了一位采用解答1的學(xué)生A來(lái)回答.

生A：就是把滿足該不等式的x的值找出來(lái).

師：是部分找出來(lái)，還是全部找出來(lái)？

生A：當(dāng)然是全部找出來(lái).

師：解答1最終把滿足不等式的x值都找出來(lái)了嗎？

生A：哦，我明白了！我是分“x>2”和“x<2”這兩段來(lái)找的，我還應(yīng)該把這兩段內(nèi)的x值“并”起來(lái).

師：你講得很對(duì)！先來(lái)看“x>2”這一段吧！那么，你把“x>2”這一段內(nèi)的x值找出來(lái)了嗎？

生A：好像還沒(méi)有.

師：“x>2”這一段內(nèi)的x要滿足什么條件？為此，你需要做點(diǎn)什么？

反思 批改作業(yè)時(shí)，筆者發(fā)現(xiàn)不少學(xué)生的解答類似于上面的解答1.表面上看是學(xué)生的能力問(wèn)題，其實(shí)，根本的原因還是學(xué)生對(duì)于“什么是解不等式”“解不等式的要求是什么”等常識(shí)性知識(shí)缺乏清晰的認(rèn)知.我們說(shuō)數(shù)學(xué)是自然的，首要表現(xiàn)在數(shù)學(xué)的思維是自然的，思維活動(dòng)引領(lǐng)下的數(shù)學(xué)方法也是自然的.要讓學(xué)生的思維自然起來(lái)，需要教師借助實(shí)例使學(xué)生感受到“從概念出發(fā)，就是按概念確定的規(guī)則辦事”和“數(shù)學(xué)概念是數(shù)學(xué)方法的源泉”，從而培養(yǎng)學(xué)生重視數(shù)學(xué)概念的學(xué)習(xí)和理解的好習(xí)慣.上面的教學(xué)中，學(xué)生一旦明白了“解不等式就是把滿足不等式的x值無(wú)一遺漏地找出來(lái)”，后續(xù)的“為什么要討論”、“何時(shí)討論”和“怎樣討論”等分類討論難題便迎刃而解.解題就像是一次遠(yuǎn)行，常常是數(shù)學(xué)概念決定了“要走怎樣的路”，以及“怎樣才算到達(dá)了目的地”.作業(yè)講評(píng)就是要讓學(xué)生的數(shù)學(xué)思維回歸自然，畢竟自然的思維是數(shù)學(xué)最本質(zhì)的東西.

課堂活動(dòng)片段之二：闡釋操作方法背后的數(shù)學(xué)思考

師：現(xiàn)在，我們來(lái)看解答2.采用這個(gè)解答的同學(xué)是怎么想的呢？

學(xué)生B不是一位采用解答2的學(xué)生，但他要求發(fā)言.

生B：我想，他是希望把這個(gè)不等式不斷地化簡(jiǎn).

師：是的.在解不等式時(shí)，我們經(jīng)常會(huì)發(fā)現(xiàn)不等式中多個(gè)位置出現(xiàn)x的情形，x隱藏得很深，而解不等式的最終要求是寫出x的取值范圍，從這個(gè)角度來(lái)說(shuō)，解不等式的過(guò)程其實(shí)是一個(gè)不斷化簡(jiǎn)的過(guò)程.為此，解答2采取了“分離常數(shù)”、“求倒數(shù)”和“兩邊同乘以一個(gè)數(shù)”等一系列步驟，不斷朝著“確定x的取值范圍”的目標(biāo)前進(jìn)，這種方法是很合理的.

師：現(xiàn)在，請(qǐng)同學(xué)們仔細(xì)檢查一下這些步驟，操作過(guò)程有什么問(wèn)題嗎？為什么？……

反思 數(shù)學(xué)方法常常表現(xiàn)為操作性步驟，數(shù)學(xué)方法的背后是數(shù)學(xué)思考.上面的講評(píng)，教師引導(dǎo)學(xué)生透過(guò)顯性的方法操作，闡釋其隱性的數(shù)學(xué)思考，并評(píng)析其合理性（或不合理性），這是保證學(xué)生思維參與并不斷深入、促使學(xué)生個(gè)體的思維向?qū)W生集體的思維轉(zhuǎn)化的教學(xué)形式，是大面積提高學(xué)生思維能力的有效舉措.從內(nèi)容上看，不同于解答1的講評(píng)，教師一針見血地指出“解不等式的過(guò)程是一個(gè)逐步化簡(jiǎn)的過(guò)程”，這就點(diǎn)出了“分離常數(shù)”、“求倒數(shù)”和“兩邊同乘以一個(gè)數(shù)”等一系列步驟的思維出發(fā)點(diǎn)，是尊重?cái)?shù)學(xué)思維的集中體現(xiàn).同時(shí)，也讓學(xué)生感受到了數(shù)學(xué)觀的教育，即“數(shù)學(xué)就是追求簡(jiǎn)單”.

課堂活動(dòng)片段之三：用數(shù)學(xué)思想開啟新思維

師：本章，我們學(xué)習(xí)了一元二次不等式的解法.把陌生的、較難的問(wèn)題轉(zhuǎn)化為熟悉的、較易的問(wèn)題，是數(shù)學(xué)中常用的思維策略.請(qǐng)同學(xué)們想一想，可以把這個(gè)分式不等式轉(zhuǎn)化為一元二次不等式來(lái)解嗎？

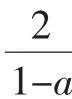
反思 抓住時(shí)機(jī)不斷推進(jìn)學(xué)生的思維發(fā)展，是發(fā)揮作業(yè)蘊(yùn)含的育人功能、體現(xiàn)教師主導(dǎo)性的重要方面.本題中，為幫助學(xué)生學(xué)會(huì)用聯(lián)系的觀點(diǎn)看待數(shù)學(xué)知識(shí)和數(shù)學(xué)方法，提升思維水平，教師及時(shí)提出了數(shù)學(xué)思想方面（轉(zhuǎn)化思想）的“學(xué)”的要求，提高了課堂講評(píng)的思想性.不僅如此，教師還對(duì)不等式轉(zhuǎn)化過(guò)程中的具體思維形式（抽象概括）給予了總結(jié)和強(qiáng)調(diào)，從而把發(fā)展學(xué)生的抽象思維意識(shí)落到了實(shí)處.

1.單墫.數(shù)學(xué)是思維的科學(xué)［J］.數(shù)學(xué)通報(bào)，2001（6）.

2.張景中，彭翕成.一線串通的初等數(shù)學(xué)［J］.數(shù)學(xué)通報(bào)，2010（2）.

3.史寧中.《數(shù)學(xué)課程標(biāo)準(zhǔn)》的若干思考［J］.數(shù)學(xué)通報(bào)，2007（5）.

4.李邦河.數(shù)的概念的發(fā)展［J］.數(shù)學(xué)通報(bào)，2009（8）.