“變”中“不變” 感受數學之靈韻

☉浙江省寧波市鄞州實驗中學 蔡衛兵

“變”中“不變” 感受數學之靈韻

☉浙江省寧波市鄞州實驗中學 蔡衛兵

習題教學是數學教學過程中不可缺少的環節，是向學生展示應用基礎知識解決問題的窗口，是向學生滲透數學思想方法、傳播解題技巧和技能的途徑.因此數學課中習題教學應該是其中的主旋律，演奏好這條主旋律更需要我們去關注習題教學過程的設計，俯視問題——用活問題，仰視學生——以生為本，為學生搭建數學學習的典型框架，讓學生主動地參與深層次的思維活動，形成基本的數學觀念，努力構建充滿靈動、富有韻味的課堂.但實際教學中，為了顯示教師的“聰明”而讓學生覺得解決問題的方法就像從魔術師的手里突然出現小白兔一樣神奇，忽略了探究過程中的輔助、轉換等環節的設計，從而出現“聽而不懂”、“懂而不會”.所以探究之路上要慢走，等一下學生，尊重學生的自我認識，尊重學生獨特的感受和經驗，讓學生獲得知識和情感的雙重體驗，讓學生收獲研究數學問題的思想和方法，讓學生在數學課堂教學中享受思維，讓我們的數學課堂靈動而不失韻味.本文就一道常見習題的教學案例及其體會與大家分享.

一、教學過程簡錄

1.霧里看花——似懂非懂

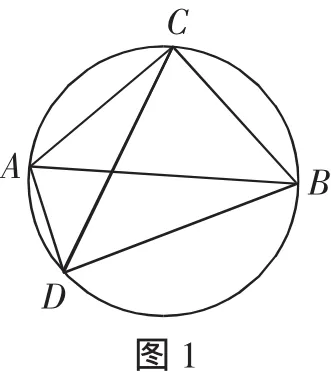
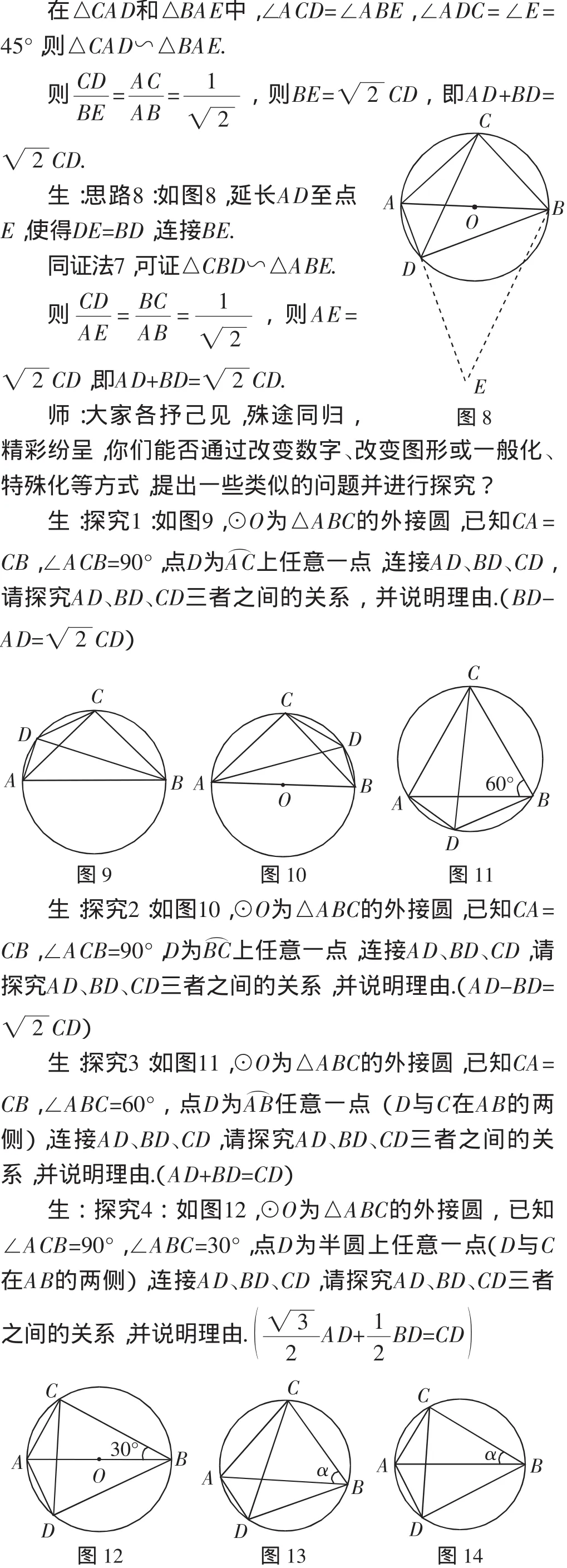
題目：如圖1，⊙O為△ABC的外接圓，已知CA=CB，∠ACB=90°，點D為半圓上任意一點（D與C在AB的兩側），連接AD、BD、CD，請探究AD、 BD、CD三者之間的關系，并說明理由.

師：請大家仔細審題.

學生審題片刻.

師：通過審題，你能獲得哪些信息？

生：等腰直角△ABC，AB為⊙O的直徑，還有∠ADC=∠BDC=45°.

師：還有補充嗎？

生：點D為半圓上任意一點.

師：根據這一信息，你如何探尋AD、BD、CD三者之間可能存在的關系呢？

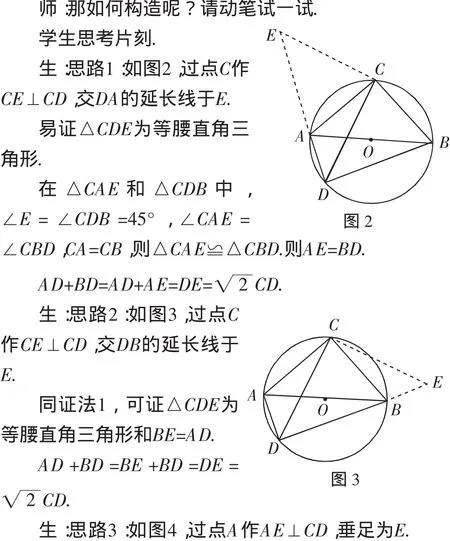
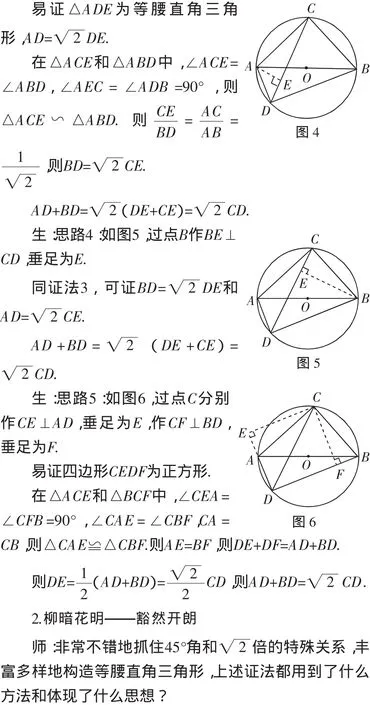
生：割補的數學方法和轉化的數學思想.

師：對于線段之間的和差關系問題，常常可用割補轉化的思想方法，我們還可以如何添輔助線呢？

生：思路6：圖還是上面幾種，比如圖2，延長DA至點E，使得AE=BD，連接CE.

在△CAE和△CDB中，CA=CB，∠CAE=∠CBD，AE=BD，則△CAE≌△CBD.

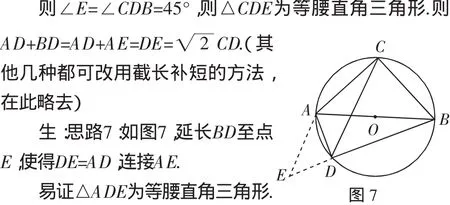
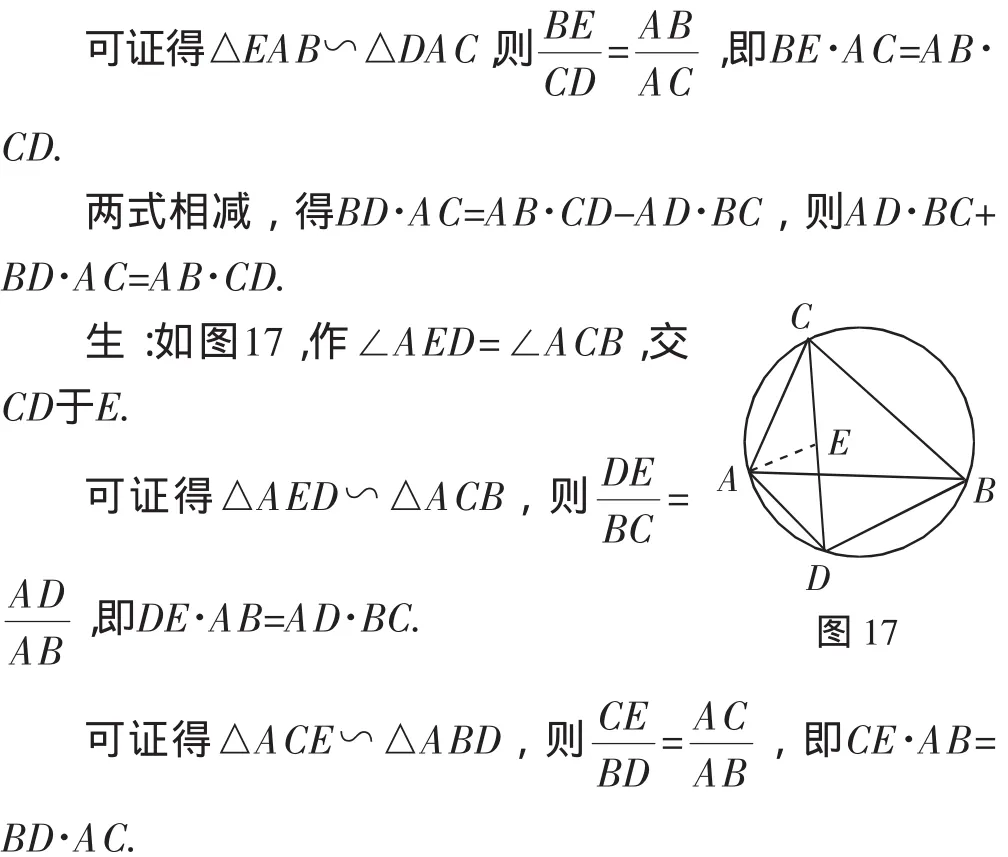
兩式相加，得AD·BC+BD·AC=AB·CD.

師：真的非常厲害，你們又是怎么想出來的呢？這里的學習又體現了什么思想方法呢？

生：其實跟原題的解題思路差不多，也是在AD、BD或CD邊上割補，原題抓住45°角構造等腰直角三角形，而構造的等腰直角三角形就是構造與△ABC相似的三角形，在這里的幾種方法也都是構造與△ABC相似的三角形，只不過用了類比的數學方法和從特殊到一般的數學思想.

師：思路很清楚，想法很深刻，總結很精彩，活學活用，那么能否用文字語言來歸納一下這個神奇的關系呢？

生：圓內接四邊形的兩條對角線的積等于兩組對邊之積的和.

師：這是一個著名的幾何定理——托勒密定理，非常佩服，其實同學們善于思考，勤于鉆研，也能像數學家一樣發現以你的名字命名的數學定理.

二、啟發與反思

1.重視學生的體驗，使課堂靈動而不失韻味

幫助學生積累數學活動經驗是數學教學的重要目標，數學活動經驗需要在“做”的過程和“思考”的過程中積淀，在數學活動中逐步積累.習題教學是知識熟練運用能力的積累，是交匯型知識綜合運用能力的積累，是思想方法滲透經驗的積累，是解決相似問題經驗的積累.本案例中，從一道常見習題的解法探究到托勒密定理的驚奇發現與多種證法，確是“千淘萬漉雖辛苦，吹盡狂沙始到金”.無論點D位置的變化中AD、BD、CD三者之間的關系的不變，還是截長補短的變化中數學思想方法的不變，無論已知條件的變化中探索AD、BD、CD三者之間的關系的不變，還是一般情形的圖形變化中構造與△ABC相似的三角形的方法的不變，學生都有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程.這樣不僅能積累數學解題經驗，而且可獲得基本的數學活動經驗，將活動經驗轉化為能力，最終獲得具有個性特征的感性認識、情感體驗、數學意識、數學能力和數學素養，這樣的課堂才是靈動而不失韻味的.

2.關注理性思維，數學課堂教學中的靈韻之筆

數學是思維的科學、思維的體操，數學的學習必須要通過思維去把握，去理解數學的實質.一題多解培養學生思維的發散性，一題多變培養學生思維的靈活性，理性思維的形成是以數學題目為載體，在題目的解決過程中形成的.本案例中，由點D為半圓上任意一點的信息的獲取，自然想到特殊值法尋找AD、BD、CD三者之間的關系，由45°角和倍的特殊關系，自然想到等腰直角三角形的構造，線段之間的和差關系問題，常常考慮用割補轉化的思想方法解決，從特殊條件到一般情形，自然想到類比構造與△ABC相似的三角形，呈現過程符合學生心理的認知規律，是合乎邏輯的思維方法，學生始終主動地參與深層次的思維活動以及數學地、合乎邏輯地、有條理地思考問題與解決問題的習慣與能力，它有明確的思維方向，有充分的思維依據，它既有發散，又有收縮，必將培養學生的運動思維，促進學生思維發展的連續性、遞進性、發展性.在教學中，教師的講解必須要貼近學生思維的發展水平，要遵循學生思維的發展規律，可使學生的認知思維過程自然流暢、水到渠成，從而能提高學生的思維能力，優化學生的思維結構.從AD、BD、CD三者之間的關系的探究到AD·BC+BD·AC=AB·CD六邊之間有著神奇而簡約的關系的發現，“形變而神不變”，經歷美妙的數學思維的歷程，呈現出數學之奇與數學之美，充分品味探究的魅力，體驗數學學習的樂趣，這是數學課堂獨特的“靈韻”之美.

1.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

2.張建良.從“看出”向“證出”提升——一道復習題教學的啟示［J］.中學數學（下），2013（10）.

3.成亮.“動中求定”感受數學之靈韻［J］.上海教育科研，2013（1）.

4.孫麟.淺談初中生數學學習經驗積累的探索［J］.中學數學（下），2013（10）.WG

·江蘇省無錫市王華民名師工作室·