例、習題的結論能否作為證明的依據——使用滬科版數學教材的幾點困惑與思考

☉安徽省當涂縣大隴初級中學 倪興隆 王小虎

例、習題的結論能否作為證明的依據
——使用滬科版數學教材的幾點困惑與思考

☉安徽省當涂縣大隴初級中學 倪興隆 王小虎

何謂證明？滬科版數學教材八年級上冊第78頁就明確規(guī)定：“從已知條件出發(fā)，依據定義、公理、已證定理，并按照邏輯規(guī)則，推導出結論，這一方法稱為演繹推理（或演繹法），演繹推理的過程，就是演繹證明，簡稱證明.”其中，定理是“從公理或其他真命題出發(fā)，用推理方法證明為正確的，并被選作判斷命題真假的依據.”通常證明有三大步驟，即：（1）根據題意，畫出圖形；（2）根據題設、結論，結合圖形，寫出已知和求證；（3）經過分析，找出由已知推出結論的途徑，寫出證明過程，并注明推理的依據.但是在使用滬科版教材（或配套教學用書）教學時，竟然發(fā)現多處運用例題或習題的結論作為證明依據的案例，給教師的教和學生的學帶來了許多困惑，現將課本原文部分摘錄，以饗讀者，供大家探討.

【案例1】滬科版教材八年級下冊第79頁例5

例題：求證：經過三角形一邊中點與另一邊平行的直線必平分第三邊.

課本中的證明過程略.

連接三角形兩邊中點的線段，叫做三角形的中位線.

關于三角形的中位線，有如下的定理.

定理：三角形兩邊中點連線平行于第三邊，并且等于第三邊的一半.

已知：如圖1，D、E分別是△ABC的邊AB、AC的中點.

同理，過點D作DF∥AC交BC于點F，則點F為BC的中點.

則四邊形DFCE為平行四邊形.

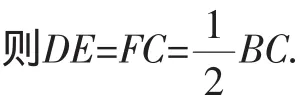
困惑：（1）定理中說“連線平行于第三邊”沒有問題，但能否說“連線”等于第三邊的一半？“連線”與“連線段”有區(qū)別嗎？

（2）教科書中用例5的結論作為三角形中位線定理證明的依據，這與教科書之前給出的證明的含義相悖，這種做法有無違背證明的邏輯規(guī)則？

思考：（1）關于“連線”與“連線段”.

連線應該是連接兩點的直線，連線段應該是連接兩點的一條線段.直線沒有長短，因此不能說連線等于第三邊的一半.而線段與直線平行不矛盾，所以本人認為定理的說法有問題，應該改為：“三角形兩邊中點的連線段平行于第三邊，并且等于第三邊的一半.”

（2）關于困惑（2）.

課本中例5實際上是平行線等分線段定理的一個推論.但滬科版教材八年級下冊第107頁A組復習題第13題，僅僅以習題的形式彰顯了平行線等分線段定理，真正以定理的形式呈現，還是在九年級上冊第61頁.

人教版教材在編排上就非常科學合理，首先編排了平行線等分線段定理和推理，繼而才有三角形中位線定理和梯形中位線定理.因此，在證明三角形中位線定理時，就不會出現上述用例題結論作證明依據的尷尬局面.

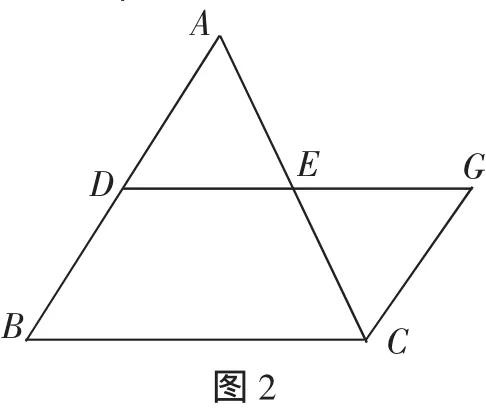
平行線等分線段定理的證明，只需要具備三角形全等的知識就足夠了，所以滬科版教材要么根據學生的認知結構，像人教版那樣調整一下編排順序，要么采用圖2的輔助線，利用全等三角形和平行四邊形的知識來證明，這樣就可避免這種令人困惑的事情發(fā)生.

【案例2】1.滬科版教材八年級下冊第100頁習題20.5第5題

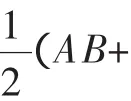
ADC）.

（2）求證：梯形的面積等于中位線與高的積.

證明過程略.

2.滬科版教材八年級下冊第110頁C組復習題第10題

習題：（1）如圖4，從◇ABCD的頂點A、B、C、D向形外的任意直線MN作垂線AA′、BB′、CC′、DD′，垂足分別是A′、B′、C′、D′，求證：AA′+CC′=BB′+DD′.

（2）如圖5，將直線MN向上平移，使得點A在直線一側，B、C、D三點在直線的另一側，這時，從A、B、C、D向直線MN作垂線，垂足分別為點A′、B′、C′、D′，那么垂線段AA′、BB′、CC′、DD′之間存在什么關系？

（3）如圖6，再將直線MN向上平行移動，使兩側各有兩個頂點，從A、B、C、D向直線MN作垂線段AA′、BB′、CC′、DD′，它們之間又有什么關系？根據圖5、圖6寫出你的猜想，并加以證明.（圖5和圖6省略）

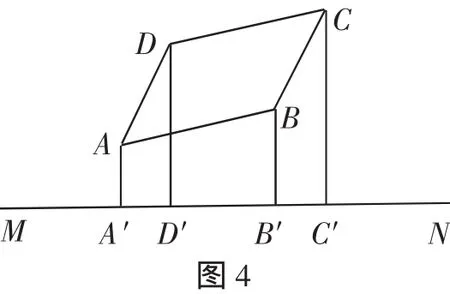
滬科版配套教學用書中的參考答案：（1）證明過程略；（2）CC′-AA′=BB′+DD′；（3）CC′-AA′=DD′-BB′.利用全等三角形或梯形中位線性質證明.

困惑：（1）上述第5題的第一問就是梯形中位線的性質定理，其他版本教材中都是以定理的形式呈現給學生的，為什么滬科版卻以習題的形式給出？在解決梯形的相關計算和證明時，能否用該習題的結論作為解題的依據呢？

（2）第5題的第二問實際上是梯形中位線定理的推論，問：在以后計算梯形面積時能否直接套用該公式？

（3）C組復習題中的第10題，雖然用三角形全等的知識能解決，但在證第二問和第三問時非常麻煩，如果采用梯形中位線的性質來證明，就簡單扼要多了.而梯形中位線的性質，課本中沒有作為定理向學生傳授，學生能用、會用或敢用嗎？

思考：（1）上百度網搜索初中常用的數學定理，明確記有平行線等分線段定理、三角形中位線定理和梯形中位線定理以及它們的推論.那么，滬科版教材為什么不能將梯形中位線性質及推論以定理的形式呈現給學生呢？

（2）根據學生現有的認知結構，完全可以將這些定理及推論編排在平行四邊形和梯形的學習內容中.這樣既可以為學生的解題提供簡潔、快捷的方法，也可以開發(fā)學生的思維，拓展學生的知識面.

（3）滬科版教材其課程內容沒有呈現部分定理和推論，估計是受到課程標準的影響.筆者仔細閱讀課程標準，發(fā)現課程內容中只是安排了“探索并證明三角形的中位線定理”，而沒有設計與梯形相關的知識內容.但是，課程標準又明確規(guī)定，教材編寫應體現科學性和整體性，教材的整體設計要呈現不同數學知識之間的關聯.一些數學知識之間存在邏輯順序，教材編寫應有利于學生感悟這種順序.

（4）滬科版教材既然已經將梯形作為一個單元編排在課本內容當中，并將梯形中位線定理設計于習題之中，就不妨按照“平行線等分線段定理及推論——三角形中位線定理——梯形中位線定理及推論——例、習題”的邏輯順序來設計教材內容，這樣就不會出現運用例、習題的結論來作為證明依據而有違邏輯規(guī)則的事情了.

數學教材為學生的數學學習活動提供了學習主題、基本線索和知識結構，是實現數學課程目標、實施數學教學的重要資源.雖然教材編排提倡凸顯特色，積極探索教材的多樣化，但是，必須在不違背數學知識邏輯關系的基礎上，根據學生的數學學習認知規(guī)律、知識背景和活動經驗，合理安排學習內容，形成自己的編排體系，體現出自己的風格和特色.同時，數學教材又是教師進行教學的重要資源，是專家們精挑細選出來供學生學習的材料……因此，作為教師，在理解教材時，要根據教材內容和學生的實際情況進行創(chuàng)造性地靈活運用；要讀懂知識的內在聯系，找出一條主線統(tǒng)領相關內容體系，創(chuàng)造性地引出、發(fā)現并證明結論.

以上觀點不知是否正確，敬請各位專家同仁批評斧正！

1.陳金紅.“理解教材”的靈動思考與教學創(chuàng)新［J］.中學數學（下），2013（8）.

2.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

3.義務教育課程標準實驗教科書·數學·八年級·下冊［M］.上海：上海科學技術出版社，2009.