山地城市應急救護中心選址研究

熊周年，宋永朝

(重慶交通大學 交通運輸學院，重慶 400074)*

0 引言

中國位居世界兩大地震帶——歐亞地震帶與環太平洋地震帶之間，受印度板塊與菲律賓海板塊還有太平洋板塊的擠壓，地震斷裂帶極多而且活躍.上世紀90年代以來，我國一共發生6級以上地震近800次，其范圍遍布除浙江與貴州及香港特別行政區以外所有的省、自治區、直轄市.地震這種自然災害的頻發性和嚴重性是我國的一大基本國情.而由于山地城市路網的特殊性，在地震來臨后道路的破壞使救援工作無法及時進行，這樣找出一個地點設立應急救護中心使其能在震后能順利到達最多地方進行救護工作就十分必要了.

對于城市路網的震后連通性國內外已經有了部分研究.早在 1982年日本學者 Kawai和Mine［1］就初次提出了連通可靠度的概念，而后國內的宋建學［2］對震后城市交通系統的連通性進行了模擬，陶小林［3］就山地城市的特征對比平原地區城市差異的基礎上對倒塌模型進行了改進.筆者在此基礎上運用蒙特卡羅法對震后山區路網連通性進行模擬，分析其連通概率，以此為基礎為應急救護中心的選址提供依據.

1 山地城市道路連通率計算

連通率又可以叫做連通可靠度，它是評價路網可靠性的一項重要指標.它可以評估出災后路網任意兩節的連通程度，為災后的救援工作提出幫助.山區路網有別于平原城市是由:路段，橋梁，邊坡，隧道等組成的一個復雜的系統，山地城市道路連通率的計算可以反映出路網在災害下任意相鄰節點間的連通情況.

在平原地區路網的組成主要為:道路和橋梁.其道路的聯通概率計算式為:

式中:P為道路連通率;Pw為路段單元通行概率;Pb為橋梁單元通行概率.

而山地城市的路網組成因其地形的復雜性而不同，其路網組成通常包括:路段，橋梁，邊坡，隧道等，串聯而成.所以道路的連通率的計算公式為

式中:P為道路連通率;Pw為路段單元通行概率;Pb為橋梁單元通行概率;Ps為邊坡單元通行概率;Pt為隧道單元通行概率

關于路段單元，橋梁單元，邊坡單元，隧道單元的通行概率計算;宋建學等［2］提出了關于災后道路沿線建筑倒塌后的瓦礫阻塞量預測模型，陶小林［3］提出了具體計算方法.

2 復雜網絡可靠性指標求取方法

復雜網絡的可靠指標求取方法主要有兩種解析法與蒙特卡羅模擬法.解析法在實際的工作中使用較多，因為使用數學模型可以準確描述出系統與子系統之間的關系，這樣可以大規模評估系統的可靠指標.它的數學模型精度高可以評估可靠指標的平均值和期望，但其計算隨著系統規模的增大而變得龐大.當網絡較為龐大和復雜時將難以計算，而這時用蒙特卡洛法進行計算機的模擬分析將較為方便.

2.1 蒙特卡羅法

概率論中講到:當所研究的樣本數量趨于無窮大時，頻率就等于概率.蒙特卡羅模擬法就是利用此結論，假如采用隨機抽樣的頻率來作為概率的近似值.其分析方法是通過計算處于連通狀態的源點與匯點的連通頻率，并以這一近似頻率計算代替精確概率分析.

2.2 蒙特卡羅模擬法分析步驟

(1)對網絡圖各節點進行編號，有關聯性的兩節點間用0～1的數來表示節點之間的可靠性數值.

(2)由節點間的可靠性數值和節點之間的關系建立關聯矩陣Qij:

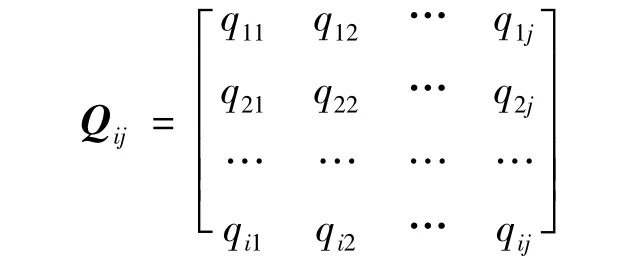
式中:當i=j時，qij=1;當節點間相關聯時，0≤qij≤1;當節點間不相關聯時，qij=0.

(3)設置隨機樣本值矩陣:Xij，并計算Aij=Qij-Xij;

(4)如果Aij＞0，則Aij=1;則表示節點i在經過若干條道路后可通往節點j;如果Aij=0，則表示節點i在此路網中無法到達節點j.

(5)重復(2)～(4)步驟，然后進行N次這樣的重復試驗，若n次后連通，則可以得出該路網的可靠性描述，源點與匯點之間的連通可靠度(連通概率)R≈n/N.

利用上述步驟進行重復計算，當計算的次數越多，則其從源點到匯點的連通概率會越精確，就越趨近于真實值.

3 應急救護中心選擇方法

(1)計算出路網中個路段道路連通率;

(2)以蒙特卡洛模擬法分析，在計算機上利用Matlab進行10萬次模擬得出路網連通可靠度;

(3)以路網中任意節點作為應急救護中心選址地點，分析改交叉口是否為最佳選擇地點，使其能在災后作為應急救護中心時能夠到達路網中的其他節點的數量最多，則選該點作為應急救護中心.選址步驟為:①假定路網中任意一個節點作為應急救護中心，用蒙特卡洛法計算出該節點到其他節點的連通率;②用上述方法計算出所有節點連通率，并統計出各節點至其他節點連通率的均值和方差，均值最大表示改節點震后能到達的節點越多，方差越小表示該節點到達其他節點的概率偏差較小.所以最后結果取均值較大方差相對較小的點.

4 重慶某區域路網算例

4.1 研究區域地形地貌及路網特征

本文所研究的路網是重慶市某區域路網.首先來介紹一下研究區域地形地貌及路網特征:

本文所研究的區域屬于重慶市某區域路網，地處銅鑼山以西、長江以南、巴南區以北，地處川東平行嶺谷區，背斜、向斜平行散布.因背斜成山，向斜成谷，是以形成低山、丘陵、平壩、河谷的組合地貌特征.重慶某區域內山地和丘陵大量散布，且一般海拔在200～500 m之間.正因山地丘陵大量散布，導致本區域內地形起伏較大，故其路網形式以自由式路網結構為主.在這種地形變化較大區域中進行道路選線時，為達到降低縱坡的目的，通常利用延長道路長度去克服自然高差，結合地形沿河岸或山麓布置，從而導致道路蜿蜒曲折且無固定的幾何類型.如圖1所示.

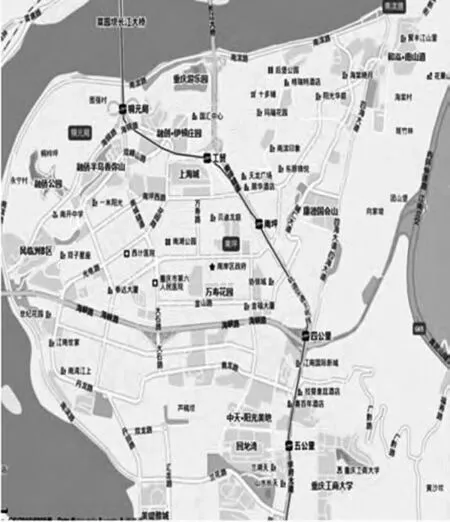
圖1 重慶市某區域路網

4.2 研究區域路網結構圖

圖2為根據重慶某區域路網圖繪制的區域路網結構圖，用來進行路網連通度分析.是按照重慶市某區域路網地圖，選取研究區域內的主干道和次干道繪制而成的.圖中用小寫數字標記的點為道路之間的交點即節點;用帶圈數字標記的為研究路段代號.由圖2可知，研究對象路網包括節點33個，路段52條.

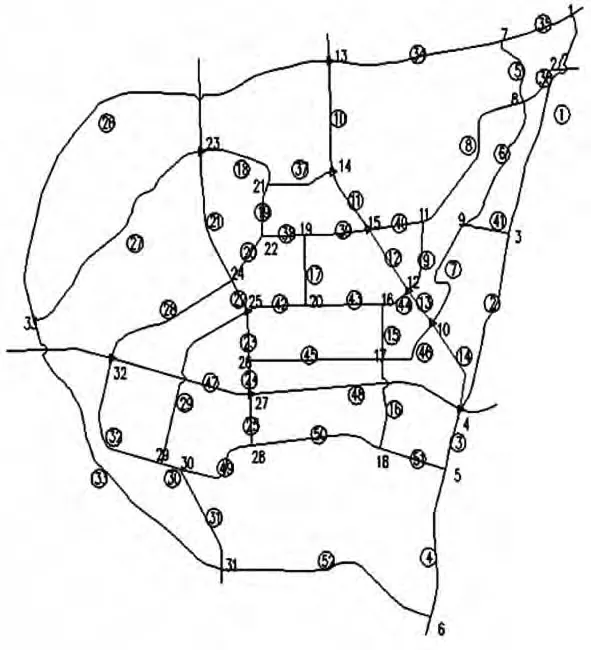
圖2 重慶市某區域路網結構圖

4.3 計算出路網中各道路連通率

通過計算，得出各個路段的連通率如表1所示，因文章篇幅所限，本文只給出部分樣例數據.

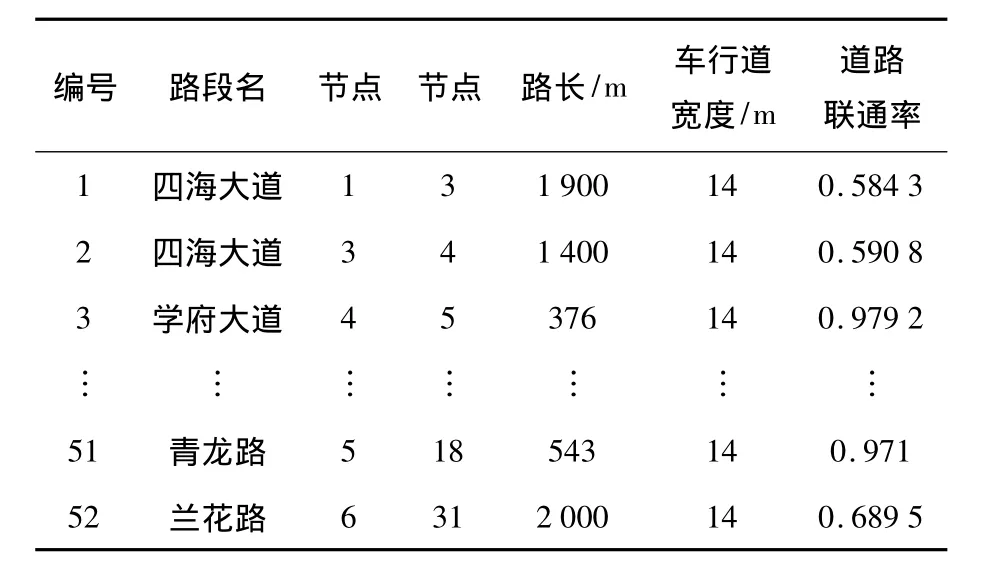
表1 重慶某區域路網道路連通率

4.4 運用蒙特卡羅法在Matlab上進行計算

計算結果如表2所示.由表2可以得出均值最大 的 點 有 14(0.969315，0.012 875)33(0.969315，0.012 875)，節點 14 與節點 15 的方差均為 0.012 875與 33個節點的方差均值0.012638出入1.876%相差較小，考慮到節點14較節點33處于路網中心，所以應急救護中心可以選擇在節點14處.如果經費允許的情況下節點14和33處都應建立一個應急救護中心.

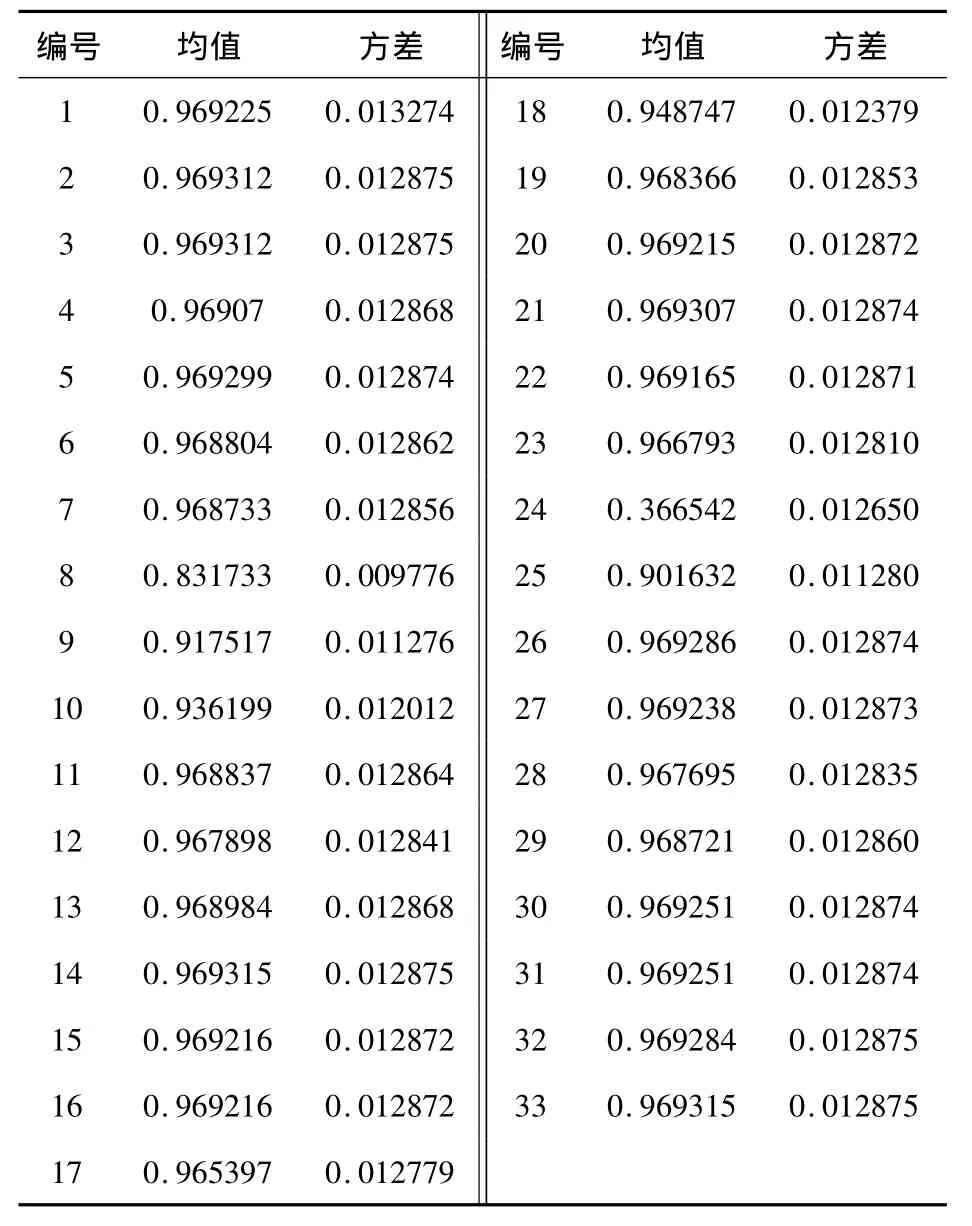
表2 各節點至其他節點連通率的均值和方差

5 結論

(1)對比了平原城市與山地城市道路連通率計算方法的不同，提出山地城市道路連通率計算應按串聯的方式考慮:路段，橋梁，隧道，邊坡等;

(2)對于路網的可靠指標可以用解析法和蒙特卡羅法進行分析.在復雜網絡中運用蒙特卡羅法模擬出路網中各個節點到其他節點的道路聯通率;

(3)以重慶南岸區為例子闡述了應急救護中心的選址過程，其結果以均值和方差來進行分析，取均值最大方差相對較小的點作為應急救護中心的選址地點.

［1］MINE H，KAWAI H.Mathematics for reliability analysis［M］.Tokyo:Asakura-shorten，1982.

［2］宋建學，李杰.震后城市交通系統連通性模擬［J］.自然災害學報，1996，5(1):73-78.

［3］陶小林.山地城市交通系統震害預測及應用研究［D］.重慶:重慶大學，2007.

［4］金國梁.生命線工程網絡震害預測方法討論［J］.工程抗震，1994，12(4):32-36.

［5］李英民，王麗萍，劉立平.山地城市交通系統震害預測模型及其應用［J］.西南交通大學學報，2009，44(2):171-176.

［6］柳春光，杜瑋，瞿桐.城市交通系統抗震可靠性研究［J］.地震工程與工程振動，1999，19(2):95-99.

［7］覃子建.20世紀地震災害概述及預測預防［J］.中國災害，2000，10(10):32-35.

［8］宋建學.地震災場模擬與模擬控制理論研究［D］.鄭州:鄭州工學院，1995.