風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)中風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重的重構(gòu)與修正研究——基于條件概率和貝葉斯定理
○董麗虹
(人民銀行銀川中心支行內(nèi)審處 寧夏 銀川 750001)
一、引言
國際內(nèi)部審計(jì)實(shí)務(wù)標(biāo)準(zhǔn)及其最新發(fā)展趨勢表明,內(nèi)部審計(jì)應(yīng)采用風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)理論和方法,更好地履行內(nèi)部審計(jì)職能。風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)是內(nèi)部審計(jì)人員通過對被審計(jì)對象風(fēng)險(xiǎn)的分析與評價(jià),全面把握被審計(jì)對象的風(fēng)險(xiǎn)狀況,根據(jù)量化風(fēng)險(xiǎn)水平識別高風(fēng)險(xiǎn)領(lǐng)域,在此基礎(chǔ)上確定審計(jì)重點(diǎn)和頻率,以便合理配置審計(jì)資源和協(xié)助管理風(fēng)險(xiǎn),實(shí)現(xiàn)審計(jì)價(jià)值增值的獨(dú)立、客觀的簽證和咨詢活動(dòng)。近年來,我國學(xué)術(shù)界就風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)做了大量的研究,深入闡述了風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)的涵義、特征,并結(jié)合當(dāng)前我國內(nèi)部審計(jì)的現(xiàn)狀,提出了推進(jìn)風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)模式應(yīng)用的策略。
人民銀行開展風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)是與國際先進(jìn)審計(jì)標(biāo)準(zhǔn)接軌的必然趨勢,也是符合央行職能轉(zhuǎn)變和業(yè)務(wù)發(fā)展需要的必然要求。《人民銀行內(nèi)審工作轉(zhuǎn)型2011—2013年規(guī)劃》的制定積極推進(jìn)了內(nèi)審工作的轉(zhuǎn)型與發(fā)展,各基層行運(yùn)用“風(fēng)險(xiǎn)引導(dǎo)審計(jì),審計(jì)關(guān)注風(fēng)險(xiǎn)”的內(nèi)部審計(jì)理念,從實(shí)施風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)的基礎(chǔ)與環(huán)境,風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)模式的構(gòu)建以及風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)模式的應(yīng)用路徑等方面進(jìn)行了深入的探索。然而,風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)的關(guān)鍵環(huán)節(jié)是風(fēng)險(xiǎn)評估,在風(fēng)險(xiǎn)評估過程中,風(fēng)險(xiǎn)因素權(quán)重的設(shè)定對評估結(jié)果的準(zhǔn)確性起著至關(guān)重要的作用,如何驗(yàn)證權(quán)重設(shè)定的科學(xué)性和準(zhǔn)確性,并根據(jù)審計(jì)實(shí)踐對風(fēng)險(xiǎn)權(quán)重進(jìn)行重構(gòu)與修正成為我們亟待解決的難題。
二、條件概率和貝葉斯定理
根據(jù)《概率論》,采用標(biāo)準(zhǔn)差作為風(fēng)險(xiǎn)測量指標(biāo),徹底避開了先實(shí)施風(fēng)險(xiǎn)登記量化賦值,再根據(jù)量化值測量風(fēng)險(xiǎn)這種主觀性較強(qiáng)的評估模式,并在實(shí)務(wù)操作中,結(jié)合被審計(jì)主體的履職目標(biāo)進(jìn)行風(fēng)險(xiǎn)識別,梳理其各風(fēng)險(xiǎn)因素(即風(fēng)險(xiǎn)類型、風(fēng)險(xiǎn)環(huán)節(jié)和風(fēng)險(xiǎn)點(diǎn))。將概率概念納入風(fēng)險(xiǎn)分析框架,不僅有力地克服了事先給定權(quán)重的人為因素,使得審計(jì)結(jié)果更加真實(shí)可靠,也為我們的研究提供了一種啟示和思路,也就是從概率的角度,對權(quán)重進(jìn)行重構(gòu)并結(jié)合審計(jì)實(shí)踐進(jìn)行修正,以期達(dá)到更加理想的結(jié)果。本文從簡要介紹概率論和貝葉斯定理的原理和計(jì)算方法到基層央行的審計(jì)實(shí)踐,闡述了聯(lián)合概率在風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重重構(gòu)方面的應(yīng)用,以及結(jié)合具體審計(jì)實(shí)際工作運(yùn)用貝葉斯定理對這一權(quán)重進(jìn)行修正的具體方法。
貝葉斯定理機(jī)率論或概率論是研究隨機(jī)性或不確定性等現(xiàn)象的數(shù)學(xué)。人們根據(jù)不確定性信息作出推理和決策需要對各種結(jié)論的概率作出估計(jì),這類推理稱為概率推理。概率推理既是概率學(xué)和邏輯學(xué)的研究對象,也是心理學(xué)的研究對象,但研究的角度是不同的。概率學(xué)和邏輯學(xué)研究的是客觀概率推算的公式或規(guī)則,而心理學(xué)研究人們主觀概率估計(jì)的認(rèn)知加工過程規(guī)律。貝葉斯推理的問題是條件概率推理問題,這一領(lǐng)域的探討對揭示人們對概率信息的認(rèn)知加工過程與規(guī)律,指導(dǎo)人們進(jìn)行有效的學(xué)習(xí)和判斷決策都具有十分重要的理論意義和實(shí)踐意義。
1、概率的幾種表示方式
條件概率:就是事件A在另外一個(gè)事件B已經(jīng)發(fā)生條件下的發(fā)生概率。條件概率表示為P(A|B),讀作“在B條件下A的概率”。條件概率公式:
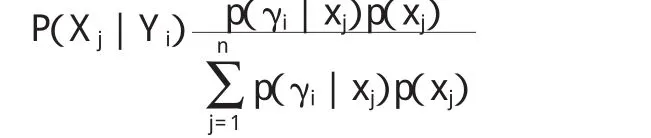
聯(lián)合概率:表示兩個(gè)事件共同發(fā)生的概率。A與B的聯(lián)合概率表示為 P(A B)或者 P(A,B)。
邊緣概率:是某個(gè)事件發(fā)生的概率,而與其它事件無關(guān)。邊緣概率是這樣得到的:在聯(lián)合概率中,把最終結(jié)果中不需要的那些事件合并成其事件的全概率而消失(對離散隨機(jī)變量用求和得全概率,對連續(xù)隨機(jī)變量用積分得全概率)。這稱為邊緣化(marginalization)。A的邊緣概率表示為P(A),B的邊緣概率表示為 P(B)。
需要注意的是,在這些定義中A與B之間不一定有因果或者時(shí)間順序關(guān)系。A可能會(huì)先于B發(fā)生,也可能相反,也可能二者同時(shí)發(fā)生。A可能會(huì)導(dǎo)致B的發(fā)生,也可能相反,也可能二者之間根本就沒有因果關(guān)系。
考慮一些可能是新的信息的概率條件性可以通過貝葉斯定理實(shí)現(xiàn)。
2、貝葉斯定理
貝葉斯定理由英國數(shù)學(xué)家貝葉斯(Thomas Bayes 1702-1761)發(fā)展,用來描述兩個(gè)條件概率之間的關(guān)系,比如P(A|B)和P(B|A)。根據(jù)《概率論》中條件概率的討論中,我們可知,在獲得新的信息之后對概率進(jìn)行修正,是一種很重要的概率分析手段。經(jīng)常地,我們開始分析時(shí),總以初始的或先驗(yàn)的概率對所關(guān)心的特殊事件進(jìn)行估計(jì),然后,我們從一些諸如樣本、報(bào)告和統(tǒng)計(jì)實(shí)踐等信息源中獲得了有關(guān)該事件的新的信息,有了這些信息,我們就能通過計(jì)算對先驗(yàn)概率值進(jìn)行修正,從而變?yōu)楹篁?yàn)概率。貝葉斯定理就是進(jìn)行這種概率計(jì)算的一種方法。
早在18世紀(jì),英國學(xué)者貝葉斯(1702—1761)曾提出計(jì)算條件概率的公式用來解決如下一類問題:假設(shè)H[,1],H[,2]…互斥且構(gòu)成一個(gè)完全事件,已知它們的概率 P(H[,i],i=1,2,…,現(xiàn)觀察到某事件 A與H[,1],H[,2]…相伴隨而出現(xiàn),且已知條件概率 P(A/H[,i]),求 P(H[,i]/A)。
貝葉斯公式(發(fā)表于 1763年)為:P(H[,i]/A)=P(H[,i])P(A│H[,i])/[P(H[,1])P(A│H[,1])+P(H[,2])P(A│H[,2])+…]
這就是著名的“貝葉斯定理”,一些文獻(xiàn)中把 P(H[,1])、P(H[,2])稱為基礎(chǔ)概率,P(A│H[,1])為擊中率,P(A│H[,2])為誤報(bào)率[1]。
三、條件概率和貝葉斯定理在風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重重構(gòu)與修正中的應(yīng)用
1、風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重的重構(gòu)
我們借鑒基層行的研究,根據(jù)被審計(jì)主題的履職目標(biāo)進(jìn)行風(fēng)險(xiǎn)識別,梳理出各風(fēng)險(xiǎn)因素(即風(fēng)險(xiǎn)類型、風(fēng)險(xiǎn)環(huán)節(jié)和風(fēng)險(xiǎn)點(diǎn))。以往的審計(jì)實(shí)踐中,對于風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重的賦值,存在較為嚴(yán)重的人為因素,使得最后的得分具有或輕或重的不可信和不可靠。所以,有必要克服風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重確定的這一人為因素。
我們知道風(fēng)險(xiǎn)環(huán)節(jié)風(fēng)險(xiǎn)權(quán)重的高低不僅受到風(fēng)險(xiǎn)點(diǎn)風(fēng)險(xiǎn)程度的影響,而且與其多少存在正相關(guān),因此,可以根據(jù)風(fēng)險(xiǎn)點(diǎn)的多少構(gòu)造風(fēng)險(xiǎn)環(huán)節(jié)與風(fēng)險(xiǎn)點(diǎn)風(fēng)險(xiǎn)情況來重構(gòu)風(fēng)險(xiǎn)環(huán)節(jié)風(fēng)險(xiǎn)權(quán)重的多少。以基層行對貨幣發(fā)行管理的審計(jì)實(shí)踐為例:如表1所示。
其中,風(fēng)險(xiǎn)點(diǎn)風(fēng)險(xiǎn)程度高、中、低個(gè)數(shù)的設(shè)定是根據(jù)審計(jì)內(nèi)容確定的。A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12分別表示“制度建設(shè)及人員配置”,“庫區(qū)設(shè)施”,“組合鎖使用管理”,“基本制度執(zhí)行情況”,“人員進(jìn)出庫區(qū)管理”,“庫存實(shí)物管理”,“出入庫業(yè)務(wù)管理”,“貨金系統(tǒng)管理”,“會(huì)計(jì)核算”,“殘損幣銷毀”,“應(yīng)急管理”,“職業(yè)道德”。
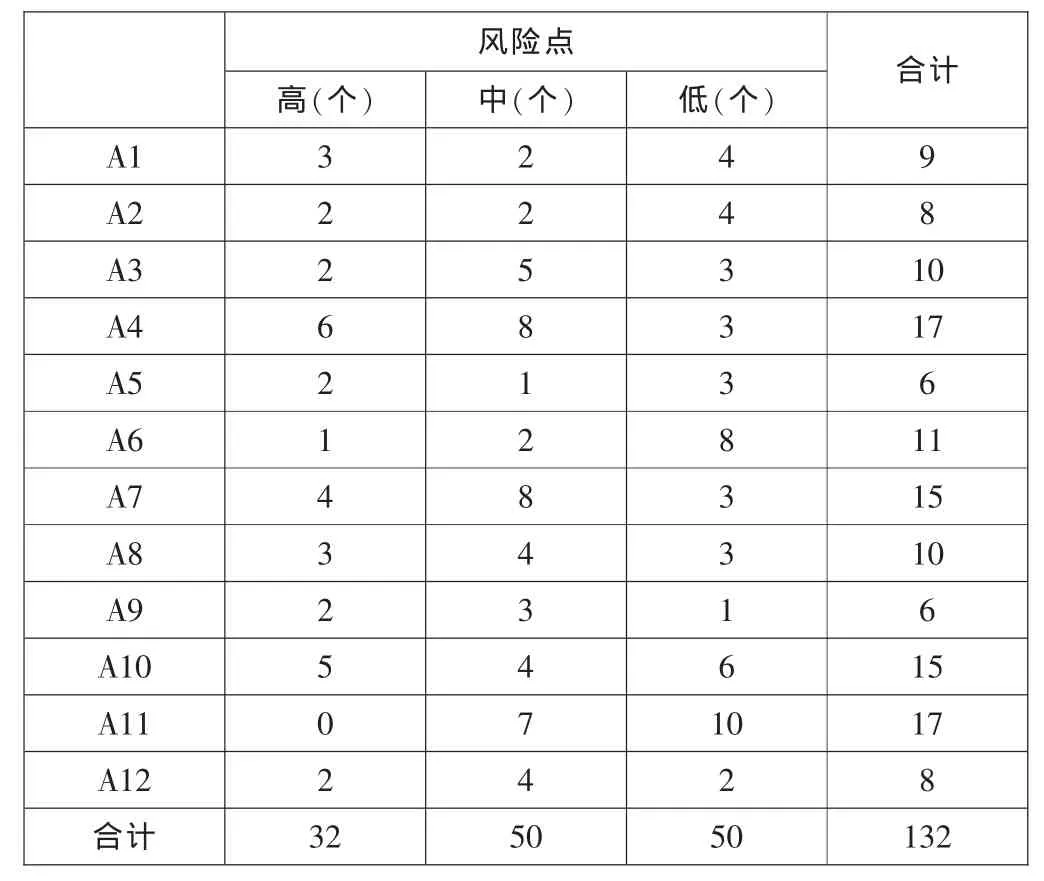
表1 風(fēng)險(xiǎn)環(huán)節(jié)與風(fēng)險(xiǎn)點(diǎn)情況表
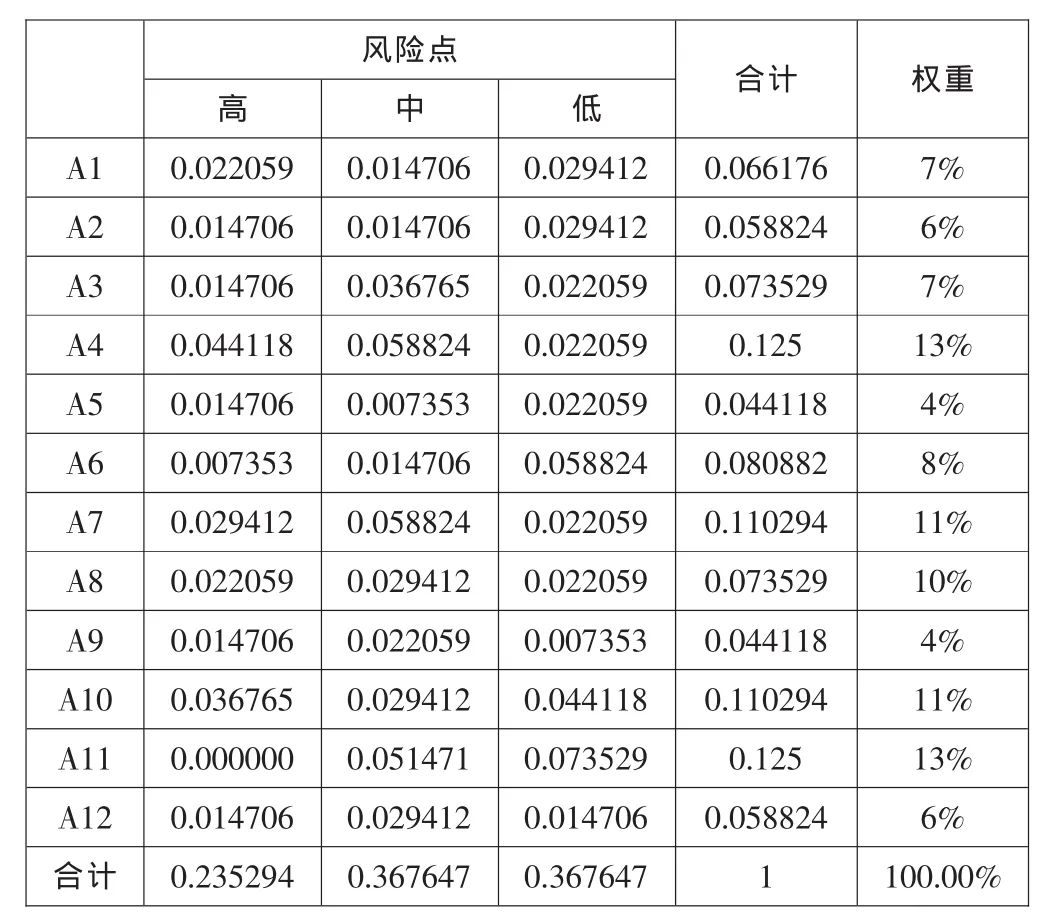
表2 風(fēng)險(xiǎn)環(huán)節(jié)與風(fēng)險(xiǎn)點(diǎn)聯(lián)合概率分布表
現(xiàn)在我們根據(jù)《概率論》中條件概率的知識,構(gòu)造表2:風(fēng)險(xiǎn)環(huán)節(jié)風(fēng)險(xiǎn)權(quán)重的聯(lián)合概率分布表。在聯(lián)合概率分布表的邊緣分別列出了每個(gè)風(fēng)險(xiǎn)環(huán)節(jié)的概率。即P(A1)=0.066176…….。這些概率就是邊際概率。根據(jù)邊際概率,我們知道7%為“制度建設(shè)及人員配置”的權(quán)重,6%為“庫區(qū)設(shè)施”的權(quán)重,7%為“組合鎖使用管理”的權(quán)重,13%為“基本制度執(zhí)行情況”的權(quán)重,4%為“人員進(jìn)出庫區(qū)管理”的權(quán)重,8%為“庫存實(shí)物管理”的權(quán)重,11%為“出入庫業(yè)務(wù)管理”的權(quán)重,10%為“貨金系統(tǒng)管理”的權(quán)重,4%為“會(huì)計(jì)核算”的權(quán)重,11%為“殘損幣銷毀”的權(quán)重,13%為“應(yīng)急管理”的權(quán)重,6%為“職業(yè)道德”的權(quán)重。
接下來的具體審計(jì)實(shí)際中,我們以此邊際概率作為各個(gè)風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重的賦值進(jìn)行分值的計(jì)算,這樣就可以避免風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重量化賦值的人為估值因素,有利于增強(qiáng)審計(jì)結(jié)果的真實(shí)性和可靠性。
2、風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重的修正
經(jīng)常地,我們開始的分析總以初始的或先驗(yàn)的概率對所關(guān)心的特殊事件進(jìn)行估計(jì),然后,我們從一些諸如樣本、報(bào)告和統(tǒng)計(jì)實(shí)踐等信息源中獲得了有關(guān)該事件的新的信息,有了這些信息,我們就能通過計(jì)算對先驗(yàn)概率值進(jìn)行修正,從而變?yōu)楹篁?yàn)概率。貝葉斯定理就是進(jìn)行這種概率計(jì)算的一種方法。用它來進(jìn)行修正概率,其步驟如圖1所示。

圖1 利用貝葉斯定理進(jìn)行概率修正
又如:在我們對國庫業(yè)務(wù)風(fēng)險(xiǎn)管理審計(jì)的研究中,我們根據(jù)我們審計(jì)的具體實(shí)際工作需要,結(jié)合多年審計(jì)實(shí)踐定義A1=“風(fēng)險(xiǎn)來自制度建設(shè)”,A2=“風(fēng)險(xiǎn)來自業(yè)務(wù)管理”,A3=“風(fēng)險(xiǎn)來自業(yè)務(wù)操作”,A4=“風(fēng)險(xiǎn)來自核算系統(tǒng)管理”,A5=“風(fēng)險(xiǎn)來自應(yīng)急管理”,A6=“風(fēng)險(xiǎn)來自道德行為規(guī)范”。根據(jù)多年的審計(jì)實(shí)踐初步設(shè)定先驗(yàn)概率 P(A1)=0.1,P(A2)=0.3,P(A3)=0.3,P(A4)=0.1,P(A5)=0.1,P(A6)=0.1。
風(fēng)險(xiǎn)的高低由于來源的不同而不同,六個(gè)風(fēng)險(xiǎn)來源的風(fēng)險(xiǎn)高低的審計(jì)實(shí)際數(shù)據(jù)見表3中。
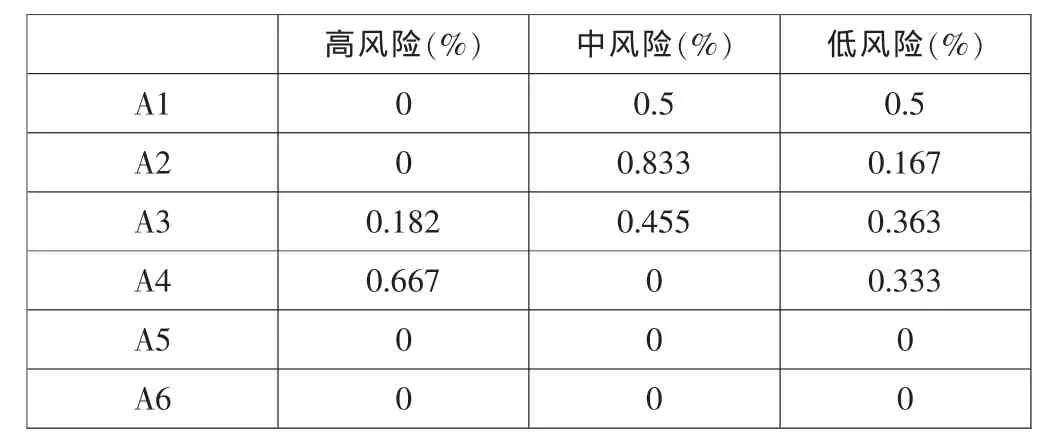
表3 風(fēng)險(xiǎn)環(huán)節(jié)的實(shí)際數(shù)據(jù)表
如果我們以G表示事件“高風(fēng)險(xiǎn)”,M表示事件“中風(fēng)險(xiǎn)”,N表示事件“低風(fēng)險(xiǎn),則表1中的信息可以用下面的條件概率來表示:
P(G—A1)=0P(M—A1)=0.5 P(N—A1)=0.5
P(G—A2)=0P(M—A2)=0.833 P(N—A2)=0.167
P(G—A3)=0.182 P(M—A3)=0.455 P(N—A3)=0.363
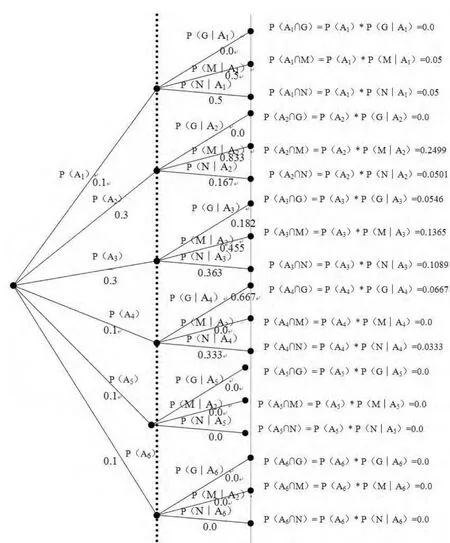
圖2 風(fēng)險(xiǎn)環(huán)節(jié)的概率樹
P(G—A4)=0.667 P(M—A4)=0P(N—A4)=0.333
P(G—A5)=0P(M—A5)=0P(N—A5)=0
P(G—A6)=0P(M—A6)=0P(N—A6)=0
我們可以用樹形圖表示這個(gè)兩步驟實(shí)驗(yàn)。我們首先從六個(gè)風(fēng)險(xiǎn)環(huán)節(jié)的某一環(huán)節(jié)出發(fā),然后再檢驗(yàn)這個(gè)風(fēng)險(xiǎn)環(huán)節(jié)里風(fēng)險(xiǎn)點(diǎn)的風(fēng)險(xiǎn)高中低。我們看到最終有18個(gè)實(shí)驗(yàn)結(jié)果。
我們看到每個(gè)實(shí)驗(yàn)結(jié)果都是兩個(gè)事件的交,可以利用乘法公式計(jì)算其概率,比如:
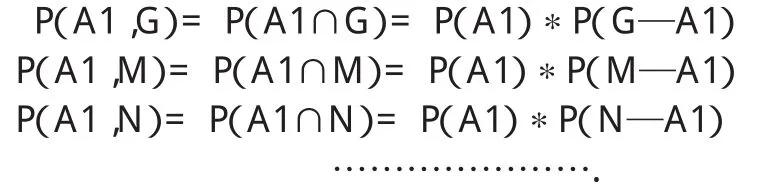
現(xiàn)在來自這六個(gè)風(fēng)險(xiǎn)環(huán)節(jié)的風(fēng)險(xiǎn)被用到審計(jì)實(shí)踐中,在已知存在風(fēng)險(xiǎn)的信息后,根據(jù)著名的“木桶原理”可以從“低”風(fēng)險(xiǎn)這一層面對來自風(fēng)險(xiǎn)環(huán)節(jié)的概率進(jìn)行修正,即“低”風(fēng)險(xiǎn)分別來自 A1,A2,A3,A4,A5,A6的概率為多少。有了概率樹上的信息(圖2),用貝葉斯定理就可以解答這樣的問題。
N表示事件“低風(fēng)險(xiǎn),我們現(xiàn)在要求后驗(yàn)概率P(A1—N),P(A2—N),P(A3—N),P(A4—N),P(A5—N),P(A6—N),從條件概率公式,我們知道

參考概率樹,我們看到
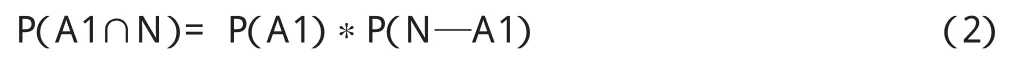
為求 P(N),我們有
P(N)=P(A1∩N)+P(A2∩N)+P(A3∩N)+P(A4∩N)+P(A5∩N)+P(A6∩N)
=P(A1)*P(N—A1)+P(A2)*P(N—A2)
+P(A3)*P(N—A3)+P(A4)*P(N—A4)
+P(A5)*P(N—A5)+P(A6)*P(N—A6)
(3)
將式(2)和式(3)代入式(1)中,并以類似方法得到 P(A2—N),P(A3—N),P(A4—N),P(A5—N),P(A6—N)的結(jié)果。
在本例中,計(jì)算結(jié)果:
P(A1—N)=0.2064
P(A2—N)=0.2068
P(A3—N)=0.4494
P(A4—N)=0.1374
P(A5—N)=0.0000
P(A6—N)=0.0000
我們注意到,開始時(shí)對于風(fēng)險(xiǎn)有0.1的概率“來自制度建設(shè)”,但是,在實(shí)際審計(jì)中給定了存在風(fēng)險(xiǎn)的信息以后,則這個(gè)風(fēng)險(xiǎn)“來自制度建設(shè)”的概率上升到了0.2064。這樣,根據(jù)修正后的風(fēng)險(xiǎn)概率和審計(jì)實(shí)際中的扣分值,按照比率計(jì)算方法,最終得到修正后的實(shí)際得分值。本例中在審計(jì)實(shí)際中,原來是按0.1的概率扣分0.3分,則按修正后的0.2064概率的扣分值為0.2064*0.3/0.1=0.6192分,進(jìn)而得到實(shí)際得分值,這樣就會(huì)得到整個(gè)風(fēng)險(xiǎn)環(huán)節(jié)的實(shí)際得分值,以此為例,被審計(jì)行按照修正后的實(shí)際分值為82分,原來按照多年審計(jì)實(shí)踐初步人為設(shè)定的概率計(jì)算的實(shí)際分值為84.3分,二者比較分值相近,這充分說明貝葉斯后驗(yàn)修正概率定理可以運(yùn)用到具體的審計(jì)實(shí)踐中,并且可以取得預(yù)期的效果。
四、結(jié)論
人民銀行開展風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)是一門新的課題,盡管近幾年來人民銀行在內(nèi)部審計(jì)實(shí)踐中就如何應(yīng)用風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)模式也摸索出了一定的方法,但是目前風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)仍然處于積極探索階段。本文從概率論中聯(lián)合概率分布和貝葉斯后驗(yàn)定理的視角,探索構(gòu)建了風(fēng)險(xiǎn)環(huán)節(jié)權(quán)重,并依據(jù)審計(jì)實(shí)際工作對其系數(shù)進(jìn)行了修正,取得了預(yù)期的結(jié)果。同時(shí),風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)也是一項(xiàng)系統(tǒng)工作,本文只是在克服根據(jù)先驗(yàn)事先給定權(quán)重的人為因素和定量評估風(fēng)險(xiǎn)環(huán)節(jié)的權(quán)重方面做了一些探索,就風(fēng)險(xiǎn)點(diǎn)風(fēng)險(xiǎn)程度高、中、低的設(shè)定也存在著一定的人為因素。因此,有關(guān)這方面的研究有待進(jìn)一步深入。
[1]劉文俊:風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)模式的應(yīng)用[J].商業(yè)會(huì)計(jì),2010(22).
[2]劉曼惠:風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)策略探析[J].現(xiàn)代商業(yè),2010(32).
[3]付春:完善風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)的應(yīng)用[J].會(huì)計(jì)之友,2009(10).
[4]李曉春、高維紅:實(shí)行風(fēng)險(xiǎn)導(dǎo)向內(nèi)部審計(jì)的難點(diǎn)和對策[J].商業(yè)會(huì)計(jì),2010(20).
[5]張?jiān)剑猴L(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)在內(nèi)部審計(jì)應(yīng)用中的探索[J].現(xiàn)代審計(jì)與經(jīng)濟(jì),2009(4).
[6]王孝玲:現(xiàn)代風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)在人民銀行內(nèi)部審計(jì)中的應(yīng)用探析[J].西部金融,2010(2).
[7]中國人民銀行武漢分行內(nèi)審處課題組:風(fēng)險(xiǎn)導(dǎo)向?qū)徲?jì)模式在人民銀行風(fēng)險(xiǎn)管理中的應(yīng)用[J].中國內(nèi)部審計(jì),2010(1).

