快速響應熱流/溫度傳感器設計與特性分析

楊慶濤，白菡塵，張濤，楊娟，王輝

(1. 中國空氣動力研究與發(fā)展中心 超高速空氣動力研究所 高超聲速沖壓發(fā)動機技術重點實驗室，四川綿陽621000;2. 中國空氣動力研究與發(fā)展中心 超高速空氣動力研究所，四川綿陽621000)

0 引言

高超聲速飛行器及其發(fā)動機在大氣層內(nèi)飛行(工作)時，結(jié)構(gòu)承受很大的熱載荷，在防熱/冷卻結(jié)構(gòu)設計時，必須清楚地掌握結(jié)構(gòu)壁面的熱環(huán)境，熱流測量是掌握壁面熱環(huán)境的常用手段［1］。

有些高超聲速飛行器地面試驗，如熱結(jié)構(gòu)考核試驗［2］、沖壓發(fā)動機燃燒組織試驗［3］、燃燒室結(jié)構(gòu)熱載荷匹配試驗［4］等，壁面熱流高(往往超過1 MW/m2)，時間長(從幾秒到上千秒)，壁面溫度會上升幾百甚至接近2 000 K. 在這些試驗中，熱流受到壁面溫度的影響，與常溫冷壁面熱流存在較大差異，因此需要掌握壁面溫度與熱流的關系。

反映壁面溫升與熱流關系的傳感器應該具備以下特點:1)響應快;2)可根據(jù)試驗時間使用若干秒到數(shù)十秒;3)結(jié)構(gòu)尺寸小(增加測點密度);4)同時測得熱流和溫度數(shù)據(jù)。

目前的熱流測量技術常用一維傳熱的假設，熱量沿壁面法向或者面向方向傳遞。根據(jù)傅里葉定律，熱量沿壁面方向傳遞時，在壁面會存在溫度梯度(如戈登計［5］)，因此無法研究壁面溫度對熱流的影響。沿法向傳遞的熱流測量技術包括瞬態(tài)測量技術［6-8］和穩(wěn)態(tài)測量技術。對于長時間、高熱流的試驗測量，瞬態(tài)測量技術不能適用。

沿法向傳遞的穩(wěn)態(tài)熱流測量技術分為兩類:1)基于能量平衡原理的水卡量熱計，其響應時間取通常從幾秒到幾十秒［9］，不能滿足快速響應的要求。2)熱阻式熱流傳感器［10-12］，通常在非金屬熱阻層兩側(cè)形成熱電偶接點，同時測得表面溫度和熱流。但非金屬熱阻層與金屬水冷或熱沉結(jié)構(gòu)連接時會存在明顯接觸熱阻，在長時間試驗中測量兆瓦平方米級熱流時，不適于兆瓦平方米級熱流、長時間的試驗［5-7］。

一些文獻基于熱阻式熱流測量原理，對在長時間試驗中的溫度和熱流測量進行了探索。文獻［13］介紹了一種柱塞式熱流傳感器，在高溫合金柱體側(cè)面安裝4 根熱電偶，測量穩(wěn)態(tài)/動態(tài)熱流，利用數(shù)據(jù)擬合獲得表面溫度，但其加工難度大，并且每個點的熱流需要測量4 個溫度數(shù)據(jù)。文獻［14］從戈登計原理出發(fā)，發(fā)展了一種水冷熱流/壁溫一體化傳感器，可以測得表面溫度和熱流，響應時間在5 s 左右。文獻［13］研究了一種用于長時間隔熱材料試驗的三段式穩(wěn)態(tài)量熱計，利用紫銅和康銅形成一種三段式結(jié)構(gòu)，在靠近交界面的紫銅上連接熱電偶，將測量的溫度近似為交界面溫度，根據(jù)溫差計算得到穩(wěn)態(tài)熱流，其響應時間不小于20 s.

針對長時間試驗中同時測量表面溫度與熱流的需求，本文設計一種新型傳感器，既能承受長時間氣動加熱，又能快速響應，反映表面溫度與熱流的對應關系。最后通過數(shù)值計算分析，驗證設計的合理性，對傳感器性能進行評價。

1 設計原理

1.1 結(jié)構(gòu)設計

針對常規(guī)熱阻式熱流傳感器的缺點，將非金屬熱阻層換為金屬熱阻層，解決與水冷結(jié)構(gòu)的連接難題。

為測量金屬熱阻層上下表面溫度，借鑒戈登計測溫原理［5］，在金屬熱阻層上下表面連接其他金屬，在兩種金屬層上分別用相應的同種材料導線連接，保持導線另一端溫度不變作為參考端，形成一種接點位于金屬熱阻層界面位置的特殊熱電偶。測量兩種金屬導線之間的電壓，可以換算得到金屬熱阻層上、下界面溫度。這樣設計的熱阻式傳感器是一種三明治結(jié)構(gòu)，中間為金屬熱阻層，上下兩側(cè)為其他金屬，見圖1 所示。

圖1 新型熱阻式熱流傳感器原理圖Fig.1 Principle diagram of novel thermal resistance type heat flux sensor

新型熱阻式熱流傳感器的中間熱阻層不再直接與加熱氣流接觸，其上界面溫度與傳感器壁面溫度不一致。為使其上界面溫度接近壁面溫度，需選用導熱率高的金屬。為獲得高靈敏度，需增大其上下溫差，應選用低導熱率金屬。考慮銅、康銅的導熱率差別(相差一個數(shù)量級)，并且二者熔點接近，易于焊接，因此選擇銅-康銅-銅作為三明治結(jié)構(gòu)新型傳感器的3 層金屬材料。

這種傳感器結(jié)構(gòu)與文獻［15］的三段式熱流傳感器相似，但利用金屬層交界面作為熱電偶接點，可避免在側(cè)面連接熱電偶，接點與金屬界面不重合造成的系統(tǒng)誤差。

1.2 數(shù)據(jù)處理方法

傳感器結(jié)構(gòu)/系統(tǒng)本身決定了熱電偶接點位置的溫度響應特性。然而，作為一個過程量，熱流取決于溫度的分布和變化，無法直接測得，只能通過測得的溫度，結(jié)合數(shù)據(jù)處理計算得到。采用不同的數(shù)據(jù)處理方法，計算所得熱流的時間響應也會不同［10，16］。同時，由于新的傳感器結(jié)構(gòu)在金屬熱阻層上界面不再與加熱氣流接觸，也不能直接測得，只能通過數(shù)據(jù)處理計算得到。只有設計適當?shù)臄?shù)據(jù)處理方法，才能得到較準確的表面溫度數(shù)據(jù)，并正確反映傳感器熱流測量的響應特性。

如圖1 所示，設傳感器壁面、康銅層上、下界面處的熱流分別為q0、q1和q2，溫度分別為T0、T1和T2. 上純銅層、康銅層的熱物性和厚度δ 分別取下標1 和2.

對于如圖1 所示的傳感器，在試驗中能夠直接測得的量是康銅層的上下界面溫度T1和T2. 通過對傳感器的傳熱模型進行分析，建立表面溫度T0和熱流q0與已測數(shù)據(jù)之間的聯(lián)系，計算得到表面溫度和熱流。

采取技術措施使傳感器側(cè)向有效絕熱，忽略側(cè)向傳熱影響，傳感器內(nèi)部熱量沿法向傳遞，為一維傳熱。根據(jù)能量守恒原理，傳感器表面的熱流，一部分通過x=δ1界面，向康銅層內(nèi)部傳遞，另一部分轉(zhuǎn)化為其他金屬層1 內(nèi)能的上升:

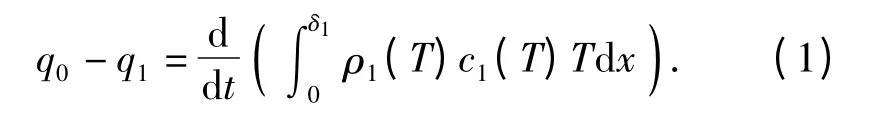
銅的導熱率很高，對于2 mm 厚的銅層，在輸入熱流為2 MW/m2時，上下溫差在穩(wěn)態(tài)時約為10℃，達到穩(wěn)態(tài)前溫差更小，物性參數(shù)的變化可以忽略［17］:

在δ1較薄時，假定溫度沿x 線性分布:

式中:A 為比例系數(shù)(K/m)。

將(3)式帶入(2)式，得

根據(jù)傅里葉定律，不同位置的熱流可以用當?shù)氐臏囟忍荻萪T/dx 來表示，有

式中:k1，0和k1，1分別為銅在溫度T0和T1時的導熱率(W/(m·K))。

在x=δ1處，有T0+Aδ1=T1，此時:

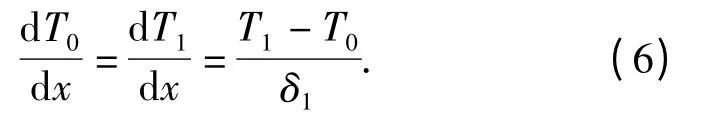
將(6)式帶入(5)式:

將(4)式與(7)式相加，整理得

根據(jù)傅里葉定律，對于0.5 mm 厚的康銅層，在輸入熱流為2 MW/m2時，其穩(wěn)態(tài)上下溫差約為27 ℃，康銅層內(nèi)ρ2c2的變化量約1.8%，導熱率k2變化量約7.9%. 可見康銅層ρ2c2的變化較小，而導熱率隨溫度的變化較大。與(1)式～(8)式類似，有

式中:k2，1和k2，2分別為康銅在溫度T1和T2時的導熱率(W/(m·K))。

聯(lián)立(4)式和(9)式，得

(10)式中包含未知量T0，因此需要進一步簡化。

銅的導熱率要比康銅高一個數(shù)量級，在δ1和δ2相近的情況下，其他金屬層1 的熱阻要遠小于康銅層。根據(jù)集總熱容法［18］，當導熱元件的內(nèi)部熱阻遠小于其相鄰熱阻時，其內(nèi)部溫度趨于均勻。另外，康銅導熱率遠小于銅，可將其他金屬層1 看做背后緊貼低導熱率材料的薄壁，在一定時間(兩種材料的熱物性比時，傅里葉數(shù)Fo==0.57)后，其上下表面的溫度變化率會趨于一致［19］。根據(jù)上述分析，一定時間以后，有dT0/dt≈dT1/dt，可將(10)式簡化為

這樣，根據(jù)(9)式與(11)式，可以計算得到q1和q0.

根據(jù)(7)式，忽略銅導熱率隨溫度的變化，計算出傳感器表面溫度T0:

得到T0后，不再采用dT0/dt≈dT1/dt 假定，利用(10)式計算q0.

在穩(wěn)態(tài)條件下，(11)式簡化為

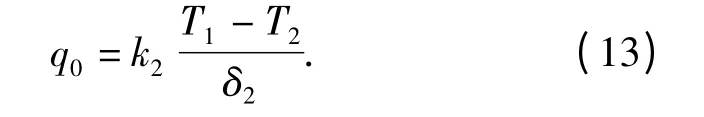
這是常規(guī)熱阻式熱流傳感器的數(shù)據(jù)處理方法［10］，只適用于穩(wěn)態(tài)熱流測量，存在水冷時，其響應時間比較長［15］。

這種傳感器量程主要取決于傳感器運行最高表面溫度限制。根據(jù)上述分析，傳感器表面溫度由輸入熱流、各金屬層尺寸和水冷條件決定。設計確定傳感器基本尺寸和水冷條件后，由傳感器表面溫度限制可以得到傳感器量程。

傳感器的測量誤差主要取決于銅-康銅測溫誤差、金屬層厚度測量誤差和熱物性近似誤差等。熱電偶測溫誤差通過標定確定，金屬層厚度測量誤差取決于長度測量方法，熱物性近似誤差取決于金屬層溫度，可分析確定。

另外，傳感器側(cè)向理想絕熱是工程上無法實現(xiàn)的，總會存在一定的側(cè)向傳熱，也會引起誤差。通過理論和數(shù)值分析，發(fā)現(xiàn)采用小長徑比的傳感器結(jié)構(gòu)、選用更小的隔熱材料、增加隔熱材料與金屬壁面間的接觸熱阻可以減小側(cè)向?qū)嵴`差。由于篇幅所限，側(cè)向隔熱層的設計及其對測量結(jié)果的影響不再贅述。

2 數(shù)值模擬驗證

2.1 數(shù)值模型及驗證

2.1.1 模型網(wǎng)格與邊界條件

利用有限元方法，對傳感器的二維瞬態(tài)傳熱模型進行數(shù)值模擬。模型網(wǎng)格如圖2 所示，選用8 節(jié)點平面四邊形單元，其他金屬層1、2 的x 向單元長度為0.04 mm，金屬熱阻層的x 向單元長度為0.01 mm. 模型共包括3 900 個單元，12 021 個節(jié)點。傳感器模型的主要尺寸見表1. 為模擬氣動加熱中壁面溫度對熱流的影響，上表面設為對流加熱條件。傳感器底部存在水冷，也設為對流換熱條件，傳感器側(cè)面設置為絕熱條件。傳感器初始溫度設為300 K.計算總時間為5 s，通過對比時間步長分別為0.020 s、0.010 s 和0.005 s 時的傳感器表面(x =0)溫升率dT0/dt(見圖3)，三者隨時間的變化曲線符合良好，考慮到計算效率，選擇時間步長0.010 s.不同算例的邊界條件設置見表2.

圖2 數(shù)值模型計算網(wǎng)格Fig.2 Computational grids of numerical model

表1 數(shù)值模型網(wǎng)格Tab.1 Sizes of the numerical model

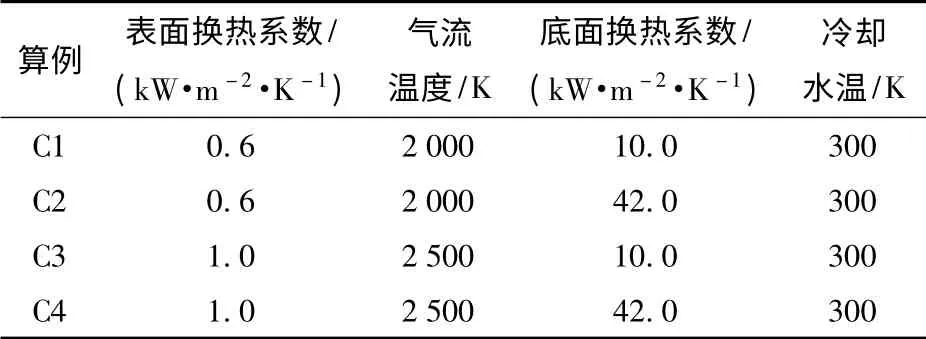
表2 算例邊界條件Tab.2 Boundary conditions for numerical cases

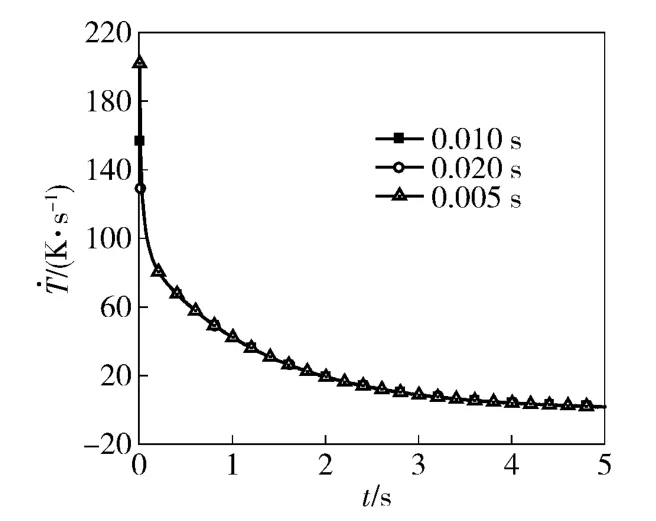
圖3 不同時間步長的表面溫升率Fig.3 Rising rates of surface temperature for different time steps

2.1.2 數(shù)值模型有效性檢驗

根據(jù)能量守恒原理對有限元傳熱分析的有效性進行定量檢驗，圍繞流進和流出任意節(jié)點能量必須保持平衡［20］，用單元熱能誤差來表示:

式中:ei為單元熱能誤差;K 為傳導矩陣;Δq 為節(jié)點熱流誤差向量;V 為單元體積。

ei越接近0，說明數(shù)值誤差越小。上述數(shù)值模型中，各算例條件下ei的最大值均小于10-10.

還可通過與理論結(jié)果的對比來驗證數(shù)值結(jié)果的有效性。在一維穩(wěn)態(tài)導熱條件下，傳感器各處溫度保持不變，根據(jù)傅里葉定律，傳感器熱流大小可以用金屬熱阻層兩側(cè)溫差來計算［1，15］。上述數(shù)值模型中忽略了側(cè)向?qū)岬挠绊懀梢院喕癁橐痪S導熱問題。在算例條件下，傳感器的穩(wěn)態(tài)軸向溫度分布見圖4.利用數(shù)值分析所得的金屬熱阻層兩側(cè)溫度，根據(jù)(13)式計算所得熱流q0與數(shù)值模擬所得表面熱流qs的相對誤差小于0.002 5%.

圖4 傳感器穩(wěn)態(tài)軸向溫度分布Fig.4 Steady axial temperature profile of sensor

對數(shù)值模型的全面驗證應與實驗結(jié)果對比，根據(jù)上述設計加工了傳感器樣件，將利用輻射加熱設備進行標定驗證，其結(jié)果將另文論述。

2.2 結(jié)果及分析

2.2.1 穩(wěn)態(tài)溫度分布

由圖4 可見，即使表面對流加熱條件相同(C1 與C2，C3 與C4)，由于底面冷卻條件不同，其表面溫度也會存在不同。輸入熱流可以利用在傳感器尺寸一定的情況下，工程上可以通過調(diào)整冷卻水壓力(流量)，改變底面冷卻條件，控制傳感器表面溫度，研究表面溫度變化與熱流的關系。

2.2.2 x 向溫度分布

圖5 為算例C1 所得傳感器x 向無量綱溫度分布(以T2為標準溫度)隨溫度的變化。利用最小二乘法分別對其他金屬層1 和康銅層溫度分布進行線性擬合，不同時刻，其他金屬層1、康銅層趨勢線與溫度分布線之間的相關系數(shù)R2見表3. 其他算例的結(jié)果與此接近。

圖5 不同時刻軸向溫度分布Fig.5 Axial temperature profiles at different times

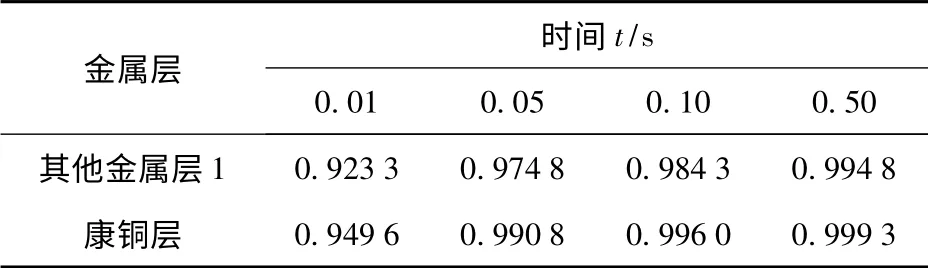
表3 溫度分布線及其擬合趨勢線的相關系數(shù)R2Tab.3 Correlation coefficients R2 of temperature profiles and their fitting trend lines

可見對于所模擬的傳感器尺寸，在初始時刻，1.2 節(jié)中溫度沿x 向線性分布的假定不夠準確，但是一定時間后，利用線性分布假定來描述金屬層內(nèi)部溫度分布是合理的。

金屬層內(nèi)部溫度分布的線性程度還與厚度有關，其他金屬層1 的溫度分布線性度比康銅層稍差，主要是因為算例中其他金屬層1 的厚度是康銅層的4 倍。

2.2.3 其他金屬層1 溫升率

算例C1 條件下Ts、T1和T2隨時間的溫升率見圖6. 由圖6 可見，在初始時刻，Ts最低，此時表面熱流最高，因此最大;隨著表面溫度的上升，輸入熱流降低，另外傳感器向底部導熱使儲能量減小，造成不斷減小。同時受上表面導熱輸入和向康銅層導熱輸出雙重因素影響，一開始輸入項占主導，增大，在0.03 s 時達到最大，之后輸出項占主導，不斷減小。Ts和T1的溫升率相對偏差在0.03 s(Fo=0.22)后小于10%，0.08 s(Fo =0.58)后小于5%，表明在一定時間以后，(11)式中關于的假定是合理的。

圖6 傳感器不同位置的溫升率Fig.6 Arising rates of temperature at different positions of heat flux sensor

2.2.4 內(nèi)部溫度響應

圖7 為算例C1 中Ts、T1、T2及表面熱流隨時間的變化。由圖7 可見，隨著表面溫度的上升，傳感器輸入熱流不斷下降，反映了壁面溫度對氣動加熱的影響。

圖7 傳感器溫度響應和表面熱流隨時間的變化Fig.7 Temperature responses and surface heat flux vs. time for the heat flux sensor

圖8為不同算例條件下的表面溫升率隨時間的變化。由圖8 可見，表面氣動加熱條件和底部水冷條件的變化都會影響傳感器的溫度響應:水冷條件相同，表面熱流越大，傳感器達到穩(wěn)態(tài)所需時間越長;表面氣動加熱條件相同，水冷越充分，傳感器達到穩(wěn)態(tài)所需時間越短。在4 個算例中，傳感器溫度達到穩(wěn)態(tài)需時間都超過了2.5 s.

2.2.5 熱流與表面溫度處理結(jié)果

圖8 不同算例條件下的表面溫升率Fig.8 Arising rates of surface temperature for different cases

圖9為分別利用(10)式和(13)式所得熱流q0m與數(shù)值結(jié)果qs的對比。由圖9 可見，利用(13)式處理數(shù)據(jù)，由于忽略了傳感器儲能的影響，所得熱流明顯滯后于實際熱流變化，不能反映表面溫度上升造成的熱流下降。而利用(10)式所得熱流q0與qs符合良好，較好地反映了表面溫度變化對輸入熱流的影響。

圖9 不同數(shù)據(jù)處理方法所得的表面熱流對比Fig.9 Comparison of surface heat fluxes achieved using different data reduction methods

定義熱流測量的相對誤差:

規(guī)定相對誤差|Er|≤2%對應的時間為數(shù)據(jù)處理所得熱流的特征響應時間。算例C1 ～C4 中，分別利用(13)式和(10)式所得到的特征響應時間見表4. 可見在算例條件下，對于所計算的傳感器尺寸，在數(shù)據(jù)處理時同時考慮溫差項與儲能項的影響，熱流的特征響應時間比穩(wěn)態(tài)處理結(jié)果小約一個數(shù)量級。

利用(12)式計算所得表面溫度T0作為根據(jù)熱阻層界面溫度測量結(jié)果處理得到的表面溫度，用數(shù)值模擬所得表面溫度Ts作為真實溫度，用二者的差T0-Ts來評價表面溫度測量結(jié)果的準確性。圖10為算例C4 中T0和Ts隨時間的變化，圖11 為不同算例條件下T0-Ts隨時間的變化。可見利用(12)式處理數(shù)據(jù)得到的溫度響應可以較好反映氣動加熱過程中壁面溫度的變化趨勢。在傳感器響應初期，由于實際溫度分布偏離線性分布較多，表面溫度誤差較大(大小與氣動加熱和水冷條件有關)，之后溫度偏差越來越小。相同加熱條件下，水冷越充分，表面溫度的處理誤差越小。

表4 不同算例的特征響應時間Tab.4 Characteristic response times for different numerical cases s

圖10 溫度處理結(jié)果Fig.10 Reduction results of temperature

圖11 表面溫度處理誤差Fig.11 Reduction errors of surface temperature

3 結(jié)論

根據(jù)上述分析，可得以下主要結(jié)論:

1)所設計的傳感器利用多層金屬作為測溫元件，在金屬層交界面上形成熱電偶接點，可避免側(cè)面連接熱電偶的定位誤差。

2)傳感器測量元件由純銅-康銅-純銅構(gòu)成，既具有高靈敏度，又可得到準確的表面溫度。

3)數(shù)值模擬結(jié)果驗證了傳感器設計和數(shù)據(jù)處理方法的合理性，表明在數(shù)據(jù)處理時同時考慮溫差項和儲能項，處理所得熱流的特征響應時間比穩(wěn)態(tài)處理結(jié)果小約一個數(shù)量級。

本文的結(jié)果只是理論和數(shù)值分析結(jié)果，傳感器的實際性能還需要進一步的實驗驗證。

References)

［1］劉初平. 氣動熱與熱防護試驗熱流測量［M］. 北京:國防工業(yè)出版社，2013.LIU Chu-ping. Heat flux measurement in aerothermodynamics and thermal protection test［M］. Beijing:National Defense Industry Press，2013.(in Chinese)

［2］陳連忠，程梅莎，洪文虎. φ1 m 電弧風洞大尺度防隔熱組件燒蝕熱結(jié)構(gòu)試驗［J］. 宇航材料工藝，2009(6):71 -73.CHEN Lian-zhong，CHENG Mei-sha，HONG Wen-hu. Ablationthermal-structure test of large scale model in φ1 m arc heated wind tunnel［J］. Aerospace Materials ＆ Technology，2009(6):71 -73. (in Chinese)

［3］江強，周樂儀，覃正，等. 液體碳氫燃料超燃沖壓發(fā)動機支板凹槽穩(wěn)焰技術試驗［J］. 推進技術，2011，32(5):680 -683.JIANG Qiang，ZHOU Le-yi，QIN Zheng，et al. Experimental investigation of strut-cavity flameholder technology in liquid hydrocarbon fueled scramjet combustor［J］. Journal of Propulsion Technology，2011，32(5):680 -683. (in Chinese)

［4］郭朝邦，李文杰，邢婭. 法國超燃沖壓發(fā)動機主動冷卻耐高溫結(jié)構(gòu)部件研究進展［J］. 飛航導彈，2011(11):84 -91.GUO Chao-bang，LI Wen-jie，XING Ya. Research advances in active cooling hot structure components of scramjet in france［J］.Aerodynamic Missile Journal，2011(11):84 -91. (in Chinese)

［5］ASTM E511-07 Standard test method for measuring heat flux using a copper-constantan circular foil，heat-flux transducer［S］.US:ASTM International，2007.

［6］Lee H J，Seung I S，Lee B J，et al. Heat flux measurement techniques over the protuberance at the hyper-sonic flow of Mach 7［C］∥16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference. Bremen，Germany:AIAA，2009:19 -22.

［7］Chadwick K M. Stagnation heat transfer measurement techniques in hypersonic shock tunnel flows over spherical segments ［R］.Buffalo，New York:AIAA，1997.

［8］Lewis D R，Norris J D. Techniques for thin-skin heat-transfer measurements for surface roughness at AEDC tunnel 9［C］∥26th AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Seattle，Washington:AIAA，2008:23 -26.

［9］ASTM E422-99 Standard test method for mea-suring heat flux using a water-cooled calorimeter［S］. US:ASTM International，1999.

［10］Kidd C T，Adams J J C. Fast-response heat-flux sensor for measurement commonality in hypersonic wind tunnels［J］. Journal of Spacecraft and Rockets，2001，38(5):719 -729.

［11］Raphael-Mabel S. Design and calibration of a novel high temperature heat flux sensor［D］. Virginia:Virginia Polytechnic Institute and State University，2005.

［12］Roediger T，Knauss H，Estorf M，et al. Hypersonic instability waves measured using fast-response heat-flux gauges［J］. Journal of Spacecraft and Rockets，2009，46(2):266 -273.

［13］Liebert C H，Kolodziej P. Dual active surface heat flux gage probe［C］∥41st International Instrumentation Symposium. Denver，Colorado:Instrument Society of America，1995:7 -11.

［14］李龍，范學軍，王晶. 高溫壁面熱流與溫度一體化測量傳感器研究［J］. 實驗流體力學，2012，26(2):93 -99.LI Long，F(xiàn)AN Xue-jun，WANG Jing. Study of integrated high temperature sensor for wall heat flux and temperature measurements［J］. Journal of Experiments in Fluid Mechanics，2012，26(2):93 -99. (in Chinese)

［15］涂建強，劉德英，陳海群. 長時間隔熱材料環(huán)境的穩(wěn)態(tài)熱流測量方法［J］. 宇航材料工藝，2008(2):76 -80.TU Jian-qiang，LIU De-ying，CHEN Hai-qun. Steady-state heatflux measurement method for environment of long-time insulation materials［J］. Aerospace Materials＆ Technology，2008(2):76-80. (in Chinese)

［16］Hubble D O，Diller T E. A hybrid method for measuring heat flux［J］. Journal of Heat Transfer，2010，132(3):031602.

［17］胡芃，陳則韶. 量熱技術和熱物性測定［M］. 第2 版. 合肥:中國科技大學出版社，2009.HU Fan，CHEN Ze-shao. Calorimetry technology and thermal physical property measurement［M］. 2nd ed. Hefei:University of Science and Technology of China Press，2009. (in Chinese)

［18］Incropera F P，DeWitt D P，Bergman T L，et al. 傳熱和傳質(zhì)基本原理［M］. 第6 版. 葉宏，葛新石，徐斌，譯. 北京:化學工業(yè)出版社，2009.Incropera F P，DeWitt D P，Bergman T L，et al. Fundermantals of heat and mass transfer［M］. 6th ed. YE Hong，GE Xin-shi，XU Bin，Translated. Beijing:Chemistry Industry Press，2009.(in Chinese)

［19］楊慶濤，白菡塵，楊娟. 薄壁量熱計后壁面導熱損失的影響及修正［C］∥第四屆高超聲速科技學術會議. 海南三亞:中國力學學會，中國科學院高超聲速科技中心，中國科學院力學研究所，高溫氣體動力學國家重點實驗室，2011.YANG Qing-tao，BAI Han-chen，YANG Juan. Influence and error correction due to heat conduction loss of thin-skin calorimeter back surface［C］∥4th Hypersonic Science and Technology Conference. Sanya，Hainan. The Chinese Society of Theoretical and Applied Mechanics，Hypersonic Research Center，CAS，Institute of Mechanics，CAS，State Key Laboratory of High Temperature Gas，2011. (in Chinese)

［20］Moaveni S. 有限元分析——ANSYS 理論與應用［M］. 歐陽宇，王崧，譯. 北京:電子工業(yè)出版社，2003.Moaveni S. Finite element analysis—ANSYS theory and application［M］. OUYANG Yu，WANG Song，translated. Beijing:Publishing House of Electronics Industry，2003. (in Chinese)