基于干擾觀測器的動力陀螺式導引頭干擾力矩補償

劉俊輝，單家元，趙新

(1.北京理工大學 宇航學院 飛行器動力學與控制教育部重點實驗室，北京100081;2.中國兵器科學研究院，北京100089)

0 引言

導引頭是尋的制導回路中的測量敏感元件，主要用于穩定探測器在空間的指向，跟蹤目標并輸出與目標視線角速度成比例的電信號［1］。彈體姿態運動產生的干擾力矩不僅會影響導引頭的跟蹤測量精度，而且使導彈制導回路中形成一個額外的隔離度寄生回路。隔離度寄生回路將直接影響導彈的制導回路穩定性及制導精度［2］。

導引頭伺服系統正常工作的前提是系統動力學穩定［3］。在導引頭系統穩定的條件下，影響導引頭跟蹤測量精度的因素主要有光學系統、探測器、力矩電機精度、電位計精度及導引頭干擾力矩等。文獻［4］分析了質量不平衡力矩、框架摩擦力矩和導線干擾力矩對制導回路的影響，并提出通過神經網絡在線辨識干擾力矩的方法來對干擾力矩進行補償。

日本學者Ohnishi 提出通過干擾觀測器(DOB)來對干擾力矩進行補償，從而提高伺服控制系統的控制精度［5］。一般通過小增益定理來確定系統穩定性，從而確定DOB 濾波時間常數選取范圍［6］。但小增益定理得出的穩定性條件是充分性而非必要性的條件，因此由小增益定理設計出的系統較保守。

本文通過設計實際的導引頭DOB 發現，通過小增益定理設計出來的系統的穩定性與仿真結果得出的穩定性差別較大。小增益定理基本不能設計合適的DOB 濾波器。文獻［6］直接將控制系統轉換到離散域進行設計，考慮了零階保持器及系統中延時的影響，但并沒有考慮多速率采樣問題。本文受文獻［7］分析制導回路中采樣保持對系統穩定性及性能影響的啟發，提出通過奈奎斯特穩定性定理來設計DOB;并考慮實際系統中的多速率采樣保持環節對系統的影響，分析獲得DOB 采樣保持和濾波器時間常數;設計出的濾波器具有較好的效果。奈奎斯特穩定性條件為充要條件，因此去除了小增益定理設計的保守性，并且還能直觀得出系統穩定的裕量。仿真結果表明了設計分析方法的有效性。

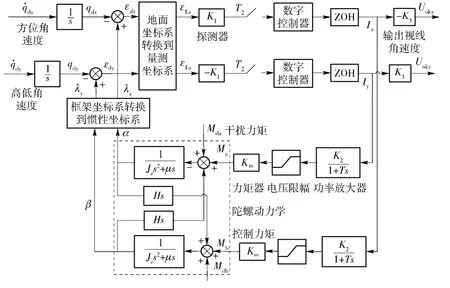
圖1 導引頭控制系統模型Fig.1 Control system model of seeker

1 導引頭及干擾力矩建模

1.1 導引頭動力學建模

建立導引頭陀螺動力學模型［1］如(1)式，為便于分析，將視線角速度在地面坐標系下描述，并考慮實際導引頭探測器不隨轉子轉動，而且視線信號為離散脈沖信號，建立導引頭控制系統模型，如圖1 所示。其中框架坐標系與量測坐標系的定義參考文獻［8］。

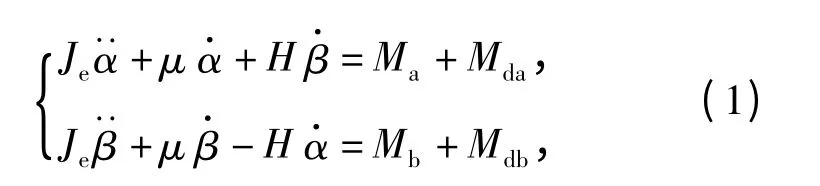
式中:α、β 分別為繞內外環轉動的角度;Je為陀螺繞內、外環框架軸的轉動慣量;μ 為粘性系數;H 為轉子的動量矩;Ma和Mb分別為加到陀螺上的控制力矩在兩框架軸方向上的分量;Mda和Mdb為干擾力矩在陀螺兩框架軸方向上的分量。圖中其余變量下角標帶d 的表示在地面坐標系下描述，下角標帶L 的表示在量測坐標系下描述。q·dx，q·dy分別為地面坐標系下方位和高低視線角速度;λ 為導引頭進動角;ε為失調角;K1為導引頭失調角到控制電流的傳遞比;K2為功率放大器放大系數;K3為視線角速度提取調整系數;Km為力矩器系數;T2為激光脈沖時間周期。

對導引頭動力學方程分析可知，方程(1)式等號左側式子中，相對于陀螺效應項，陀螺的慣性效應所產生的耦合力矩可以忽略。因此，DOB 設計時可以將導引頭控制系統進行解耦，對方位和高低通道分別進行設計。

1.2 導引頭干擾力矩模型

在工程實際中，一般通過質量配平來減小質量不平衡力矩。質量不平衡力矩通常可以減小到很小，而框架軸摩擦力矩和導線干擾力矩一般較難克服。因此本文針對導引頭框架軸摩擦力矩和導線干擾力矩進行研究分析。由于DOB 干擾力矩補償與干擾力矩模型沒有聯系，只與干擾力矩大小及帶寬有關系，因此忽略質量不平衡及其他干擾力矩是可行的。參考文獻［9］得到的摩擦力矩模型為

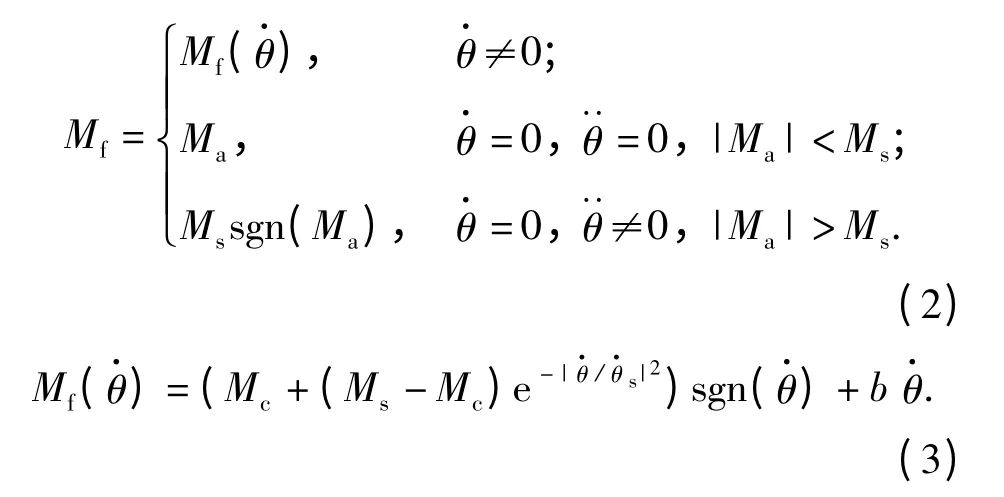
式中:Mf為框架軸摩擦力矩;Ms、Mc分別表示最大靜摩擦力矩和滑動摩擦力矩;Ma為進動力矩;分別代表相對角速度、加速度和Stribeck 速度;b代表粘滯摩擦系數;sgn 為符號函數。

導引頭通過導線為陀螺及探測器提供電能，探測器量測信號的傳遞也需要導線。由于導線一端固定于基座，一端連接于運動陀螺，因此陀螺在運動過程中導線將產生一定的干擾力矩作用于框架軸上。導線引起的非線性恢復力矩［3］可以描述為

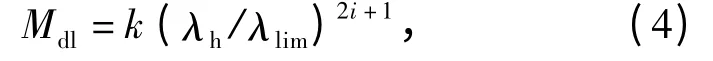
式中:k 為非線性彈簧系數;λh為框架軸相對于基座運動角度;λlim為閾值;i 為整數，常取1.

2 實用DOB 設計

2.1 導引頭DOB 設計

對導引頭控制回路進行簡化，忽略慣性耦合力矩，在縱向平面內以俯仰通道為例可以得到導引頭控制系統模型，如圖2 所示。通過簡化模型來設計導引頭DOB，如圖3 所示。

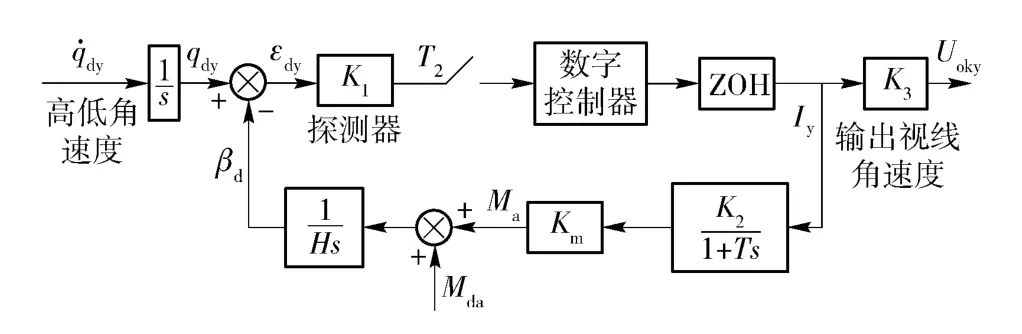
圖2 導引頭控制系統簡化模型Fig.2 Simplified control system model of seeker

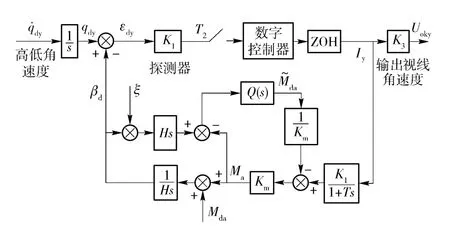
圖3 基于導引頭簡化模型的DOBFig.3 DOB of seeker based on simplified model

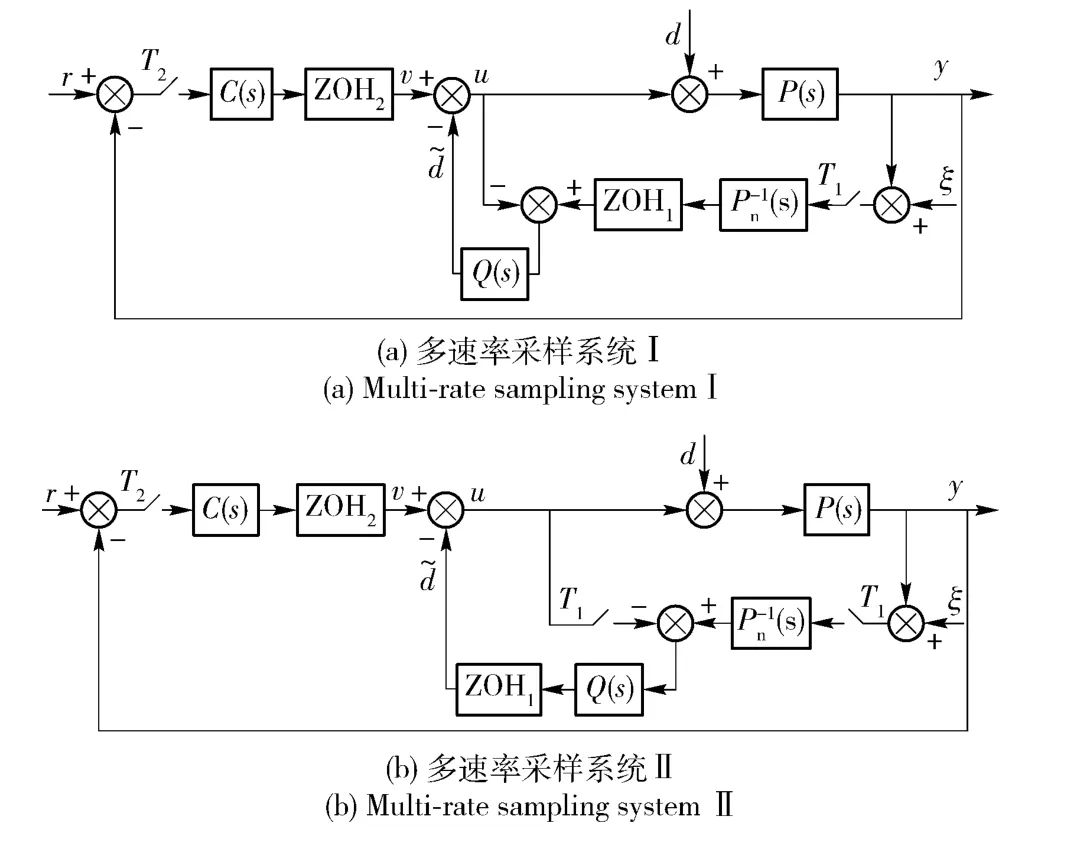
圖4 帶DOB 的多速率采樣系統Fig.4 Multi-rate sampling systems with DOB

為了將設計方法推廣到一般系統，將帶有DOB的導引頭系統模型轉化為通用模型［5-6］。圖中ξ 為進動角測量噪聲，加入位置根據導引頭的實際模型作了相應調整。考慮到實際采樣保持環節的引入點及濾波器環節實現(數字或模擬式)，設計實用DOB，如圖4(a)與圖4(b)所示。多速率采樣系統I中，逆系統的實現采用數字式，濾波器的實現采用模擬式。系統II 中逆系統及濾波器的實現均采用數字式，而且控制指令也需要進行采樣。本文通過理論與仿真分析得到系統II 的效果不如系統I，而且本質上二者都屬于多速率采樣控制系統，設計方法相同。本文只針對系統I 進行設計驗證。

2.2 導引頭DOB 參數選取

在實際控制回路中，設計DOB 前通常就已經確定系統采樣保持時間T2和控制器C(s). 通過后面的分析可知，系統控制器的設計可以與DOB 的設計分離，二者間的相互影響很小，可以忽略。因此，在控制回路中需要設計的參數為DOB 采樣保持時間T1、Q(s)的濾波時間常數以及信號通過逆系統)的處理方式。

俯仰通道上，將導引頭控制回路轉換為如圖4(a)所示的系統得到控制器

由(1)式得到實際被控對象陀螺的傳遞函數為

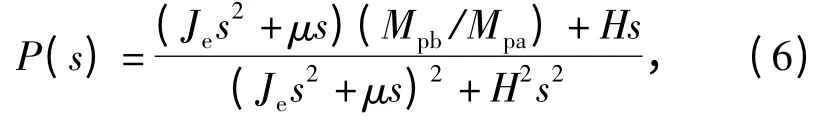
式中:Mpb=Mb+Mdb，Mpa=Ma+Mda. 考慮實際導引頭系統中的干擾力矩，得出|Mpb/Mpa| ＜12.

為了方便設計DOB，簡化實際陀螺模型，得到標稱被控對象為

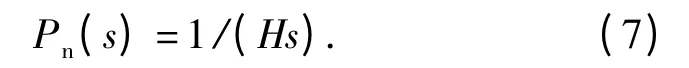
由(6)式和(7)式得到被控對象的乘性攝動為

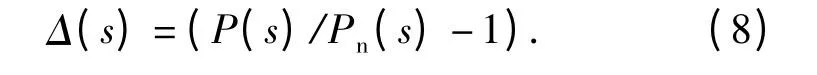
系統中的采樣開關當作理想采樣，連續系統開環傳遞函數采樣后得到［7］

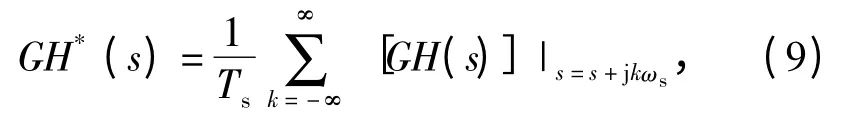
式中:Ts為采樣周期;ωs為采樣頻率。

系統中的零階保持器

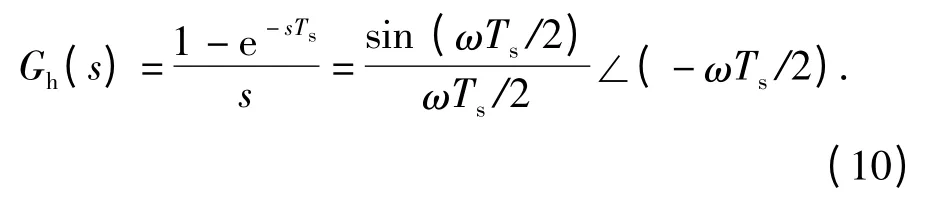
零階保持器具有低通特性，采樣系統經過零階保持器后，高頻部分將會大幅度衰減，而只保留采樣系統中的原始部分。因此經過采樣保持后的系統可以近似為

DOB 開環傳遞函數為

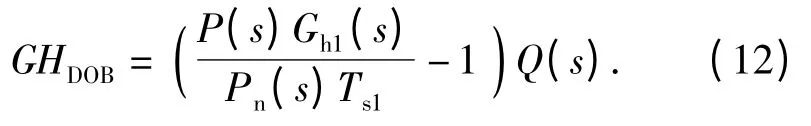
導引頭回路開環傳遞函數為

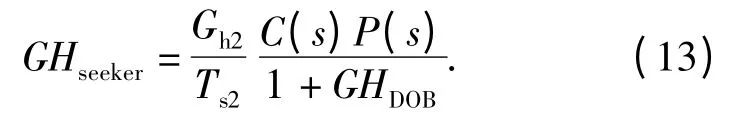
至此，帶DOB 的導引頭多速率采樣系統已轉化為連續域模型，通過繪制DOB 和系統開環傳遞函數波特圖，對DOB 響應速度、穩定裕量以及系統響應速度、噪聲抑制能力、穩定裕量進行權衡來選取系統參數，確定逆系統處理方式，以使系統性能達到最優。

連續系統中采樣保持環節的引入相當于在原有系統基礎上附加了采樣保持環節的幅值衰減和相位滯后。相位滯后與頻率呈線性關系，對系統穩定性將帶來較大影響。

DOB 中濾波器Q(s)的選取對控制系統的性能有較大的影響。常采用的濾波器如下式［10］:

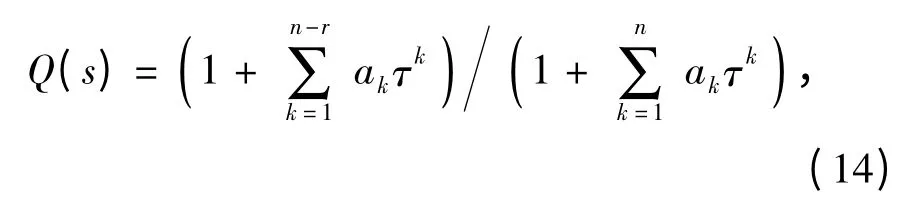
式中:n 是Q(s)的階次;τ 是濾波器時間常數;r 是Q(s)的相對階次。

考慮到實際中1 階濾波器易于實現，設計中采用1 階慣性濾波器

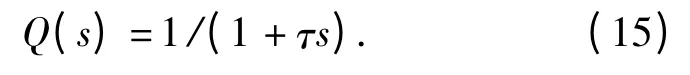
由小增益定理得到系統的穩定性條件為

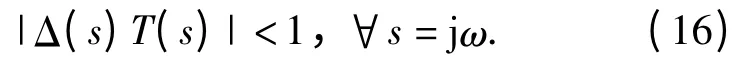
T(s)為DOB 回路或系統回路的補靈敏度函數，在兩種補靈敏度函數下系統都必須滿足(16)式才穩定。通過(16)式來確定DOB 及系統的穩定性［6］，從而設計濾波器時間常數τ. 這種方法在設計實際DOB 時，會因為小增益定理的保守性而無法獲得滿意的濾波時間常數。

導引頭系統的參數如表1 所示，導引頭采樣時間為激光脈沖周期。繪制系統圖4(a)的波特圖如圖5 所示，圖5(a)虛線為DOB 補靈敏度函數幅值，圖5(b)虛線為系統補靈敏度函數幅值。在導引頭采樣時間取0.1 s 和DOB 采樣時間取0.02 s 條件下，由小增益定理得，只有當τ≥0.7 s 時，系統才穩定，而由實際仿真可知，當τ≥0.03 s 時，系統已經穩定。小增益定理設計參數過于保守。因此提出采用奈奎斯特穩定性條件來設計濾波器時間常數τ.

在導引頭回路中，DOB 采樣保持時間與濾波時間常數對DOB 與系統的影響，如圖6 ～圖9 所示。由圖7 和圖9 可以看出，DOB 采樣時間和濾波時間常數對導引頭系統的幅值與相位特性影響很小，僅濾波時間常數對導引頭系統相位特性有所影響。其對導引頭系統的影響體現在對系統穩定裕度的影響上。因此，DOB 與系統控制器可以分離設計。

在濾波時間常數為0.2 s 條件下，DOB 采樣保持時間對DOB 和系統開環波特圖的影響，如圖6 和圖7 所示。由圖6 可以看出，隨著采樣時間的增加，DOB 低頻中頻段幅值增益增大，但始終小于0 dB.雖然高頻諧振點幅值大于0 dB，但該頻率點上的相位大于-180°，因此DOB 還有較大的幅值增益裕度。由圖7 可以得到在4 個不同采樣時間下導引頭系統都保持穩定，隨著采樣保持時間增加，系統的增益裕度與相位裕度下降。

表1 導引頭系統參數Tab.1 Parameters of seeker

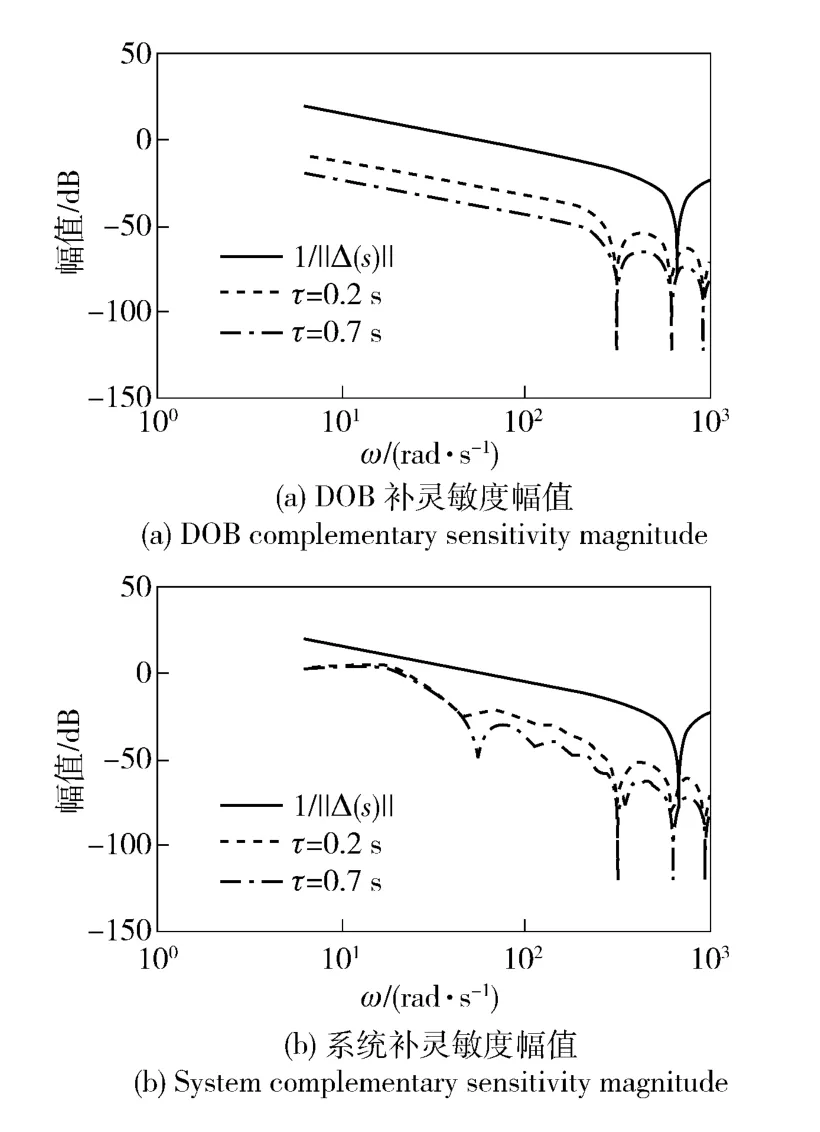
圖5 DOB 及系統補靈敏度幅值Fig.5 DOB and system complementary sensitivity magnitudes

采樣保持時間為0.02 s 時，濾波器時間常數對DOB 和系統的影響如圖8 和圖9 所示。由圖8 可知，在濾波時間常數為0.01 s 時，由于幅值裕度為負值，DOB 內回路不穩定。隨著濾波時間常數的增大，DOB 內回路穩定裕度增大。由圖9 可得，4 個時間常數下，系統都保持穩定，而且隨著濾波時間常數的增大，系統的穩定裕量增大，而響應速度有所下降。

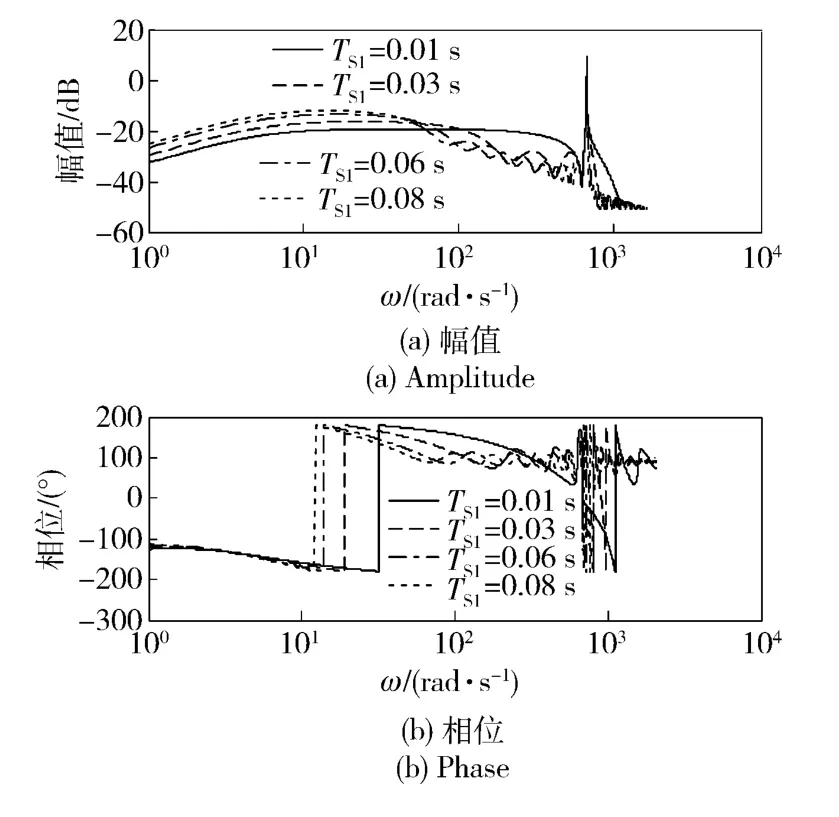
圖6 不同采樣時間下DOB 波特圖Fig.6 DOB Bode diagrams at different sampling times

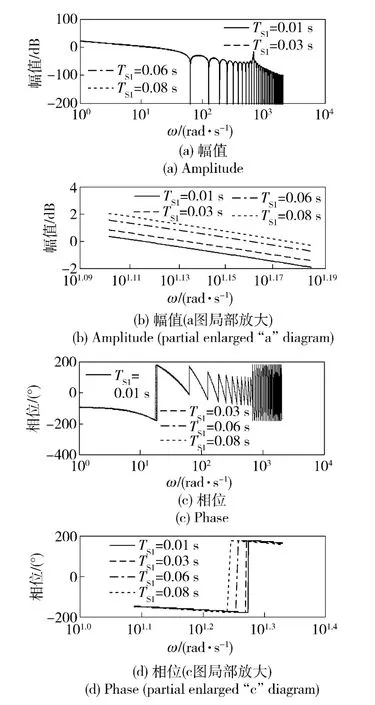
圖7 不同采樣時間下系統波特圖Fig.7 System Bode diagrams at different sampling times

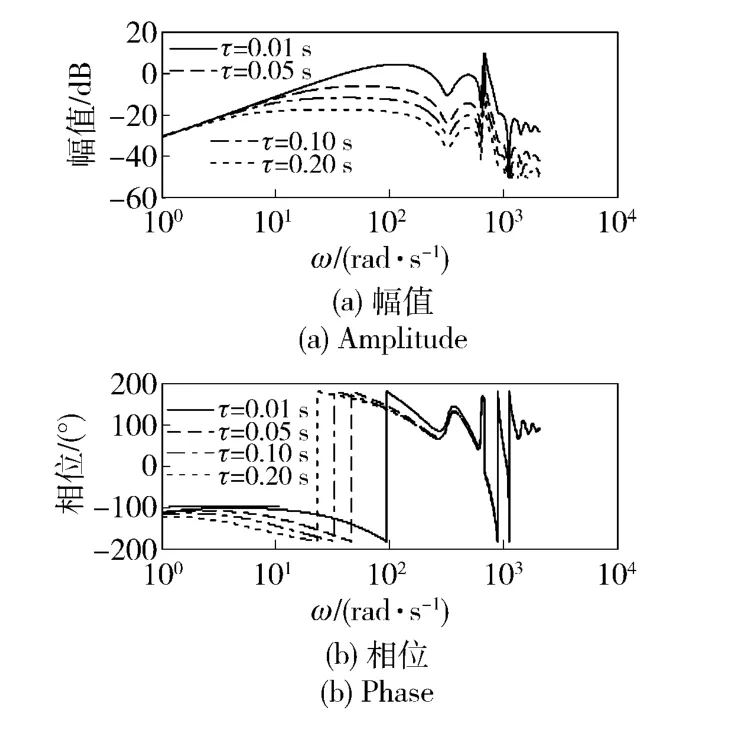
圖8 不同濾波時間常數下DOB 波特圖Fig.8 DOB Bode diagrams with different filtering time constants

為分析DOB 采樣保持時間及濾波時間常數對系統穩定性的影響，繪出了不同采樣保持時間下系統(見圖10(a)和圖10(b))及DOB 回路(見圖10(c))穩定性裕度隨濾波器時間常數的變化。由圖8 和圖10 可以看出，為保證DOB 回路穩定，濾波器時間常數需要大于0.03 s，而且隨著濾波時間常數的增大，DOB 回路的增益裕度增大，噪聲抑制能力加強。由圖9 和圖10 可以得到，隨著濾波器時間常數的增大，系統低頻增益增大，幅值裕度和相位裕度變化較緩。由圖10 可以看出，隨著采樣保持時間的增大，DOB 及系統的穩定裕度下降較快。因此綜合考慮系統穩定裕度、干擾和噪聲抑制性能及實際DOB 實現難度(主要體現在采樣保持時間的硬件實現)，選取DOB 采樣保持時間為0.02 s，濾波時間常數為0.20 s. 此時，DOB 幅值裕度為17.4 dB，系統相位裕度為27.13°，幅值裕度為3.66 dB，系統穿越頻率為13.18 rad/s.

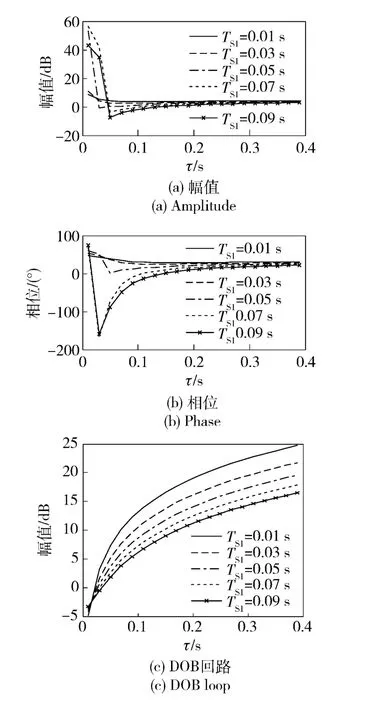
圖10 不同參數下系統穩定裕度和DOB 穩定裕度Fig.10 System stability margins and DOB stability margins with different parameters

2.3 DOB 所需信息提取

為了實現DOB，還需對逆系統進行處理。在導引頭回路中逆系統為Hs，即只需獲取進動角的微分即可。但是，在導引頭回路中進動角并不能直接獲取。導引頭是通過量測視線角與進動角之間的偏差而實現反饋控制。由于視線角不能獲取，因此不能通過視線角和失調角來獲得進動角。

與半捷聯導引頭工作原理一致，導引頭的進動角速度可以通過彈上彈體姿態信息與導引頭框架角信息來間接獲得導引頭的進動角，然后再微分獲得導引頭的進動角速度。

以高低方向為例，高低方向彈體、目標和導引頭光軸的幾何關系如圖11 所示。由幾何關系可知

式中:λy為導引頭光軸俯仰進動角;?y為彈體俯仰角;β 為導引頭俯仰框架角。

方程(17)式等號兩邊同時微分得

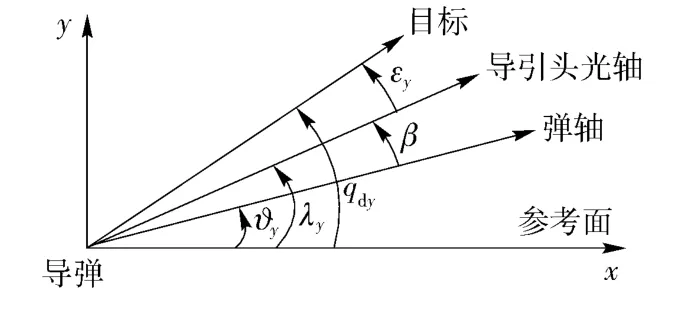
圖11 彈體、目標和導引頭光軸的幾何關系Fig.11 Geometric relation of missile，target and optic axis

一般情況下，彈體俯仰角速度和偏航角速度為自動駕駛儀使用信息，可直接利用。如果在導引頭框架軸上安裝測量角速度的裝置，那么DOB 所需的信息就可以通過彈體角速度與框架軸角速度直接求和得到。但是，在現有的型號中，導引頭通常只測框架角信息，因此需要通過微分算法來獲得框架角速度信息。

3 仿真分析

為了評價導引頭干擾力矩補償效果，使用耦合度和跟蹤精度兩個指標來對導引頭跟蹤性能進行評價。動力陀螺式導引頭耦合度定義為導引頭交叉通道的輸出幅值與導引頭輸入信號幅值之比。導引頭跟蹤精度定義為導引頭輸出幅值與目標視線角速度之間的比值。耦合度與隔離度產生的原因相同，都是由干擾力矩引起的，因此在此就不再進行隔離度的仿真。

采用前文中摩擦力矩及導線干擾力矩模型，模型中的參數通過實際數據辨識可以得到。導引頭的進動角速度通過直接數值微分獲得。傳感器噪聲模型采用均勻分布白噪聲，仿真步長及其他仿真條件如表2 所示，采用4 階龍格庫塔仿真算法。

對導引頭兩個通道同時設計DOB，采用圖1 中的模型進行仿真。仿真結果如圖12 所示，對比補償前后容易得出DOB 對干擾力矩具有較好的補償作用。補償干擾力矩后，導引頭測量耦合度由11.3%提高到5.0%，導引頭測量精度由92.5%提高到100%. 圖13 為干擾力矩補償前后陀螺的控制力矩。需要注意的是，干擾力矩的補償是以消耗控制力矩為代價的。必須保證導引頭的力矩器有足夠的控制能力，即能產生足夠控制力矩，這樣才能達到對干擾力矩進行補償的目的。

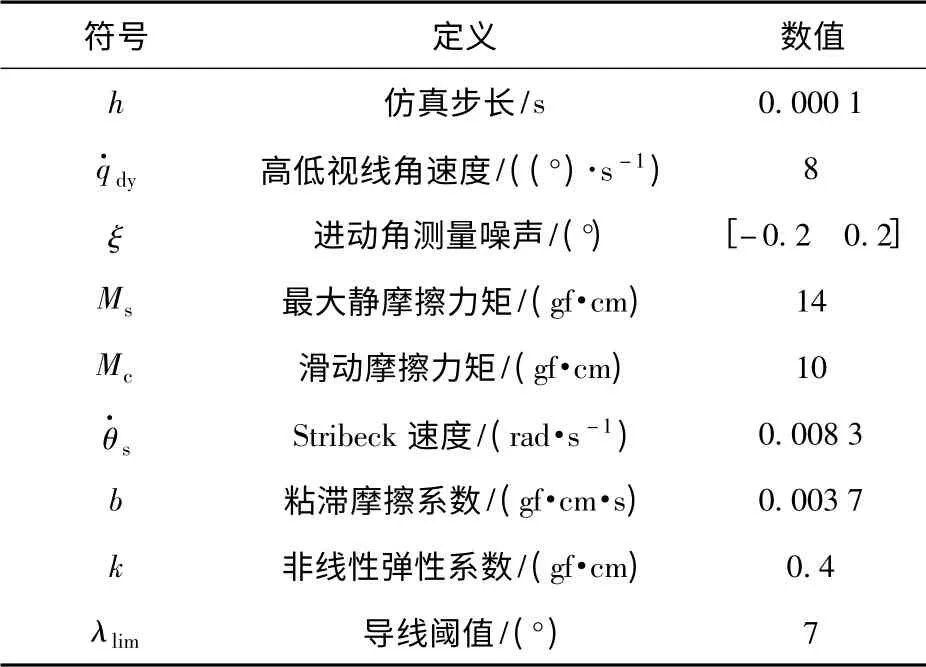
表2 仿真條件Tab.2 Simulation condition

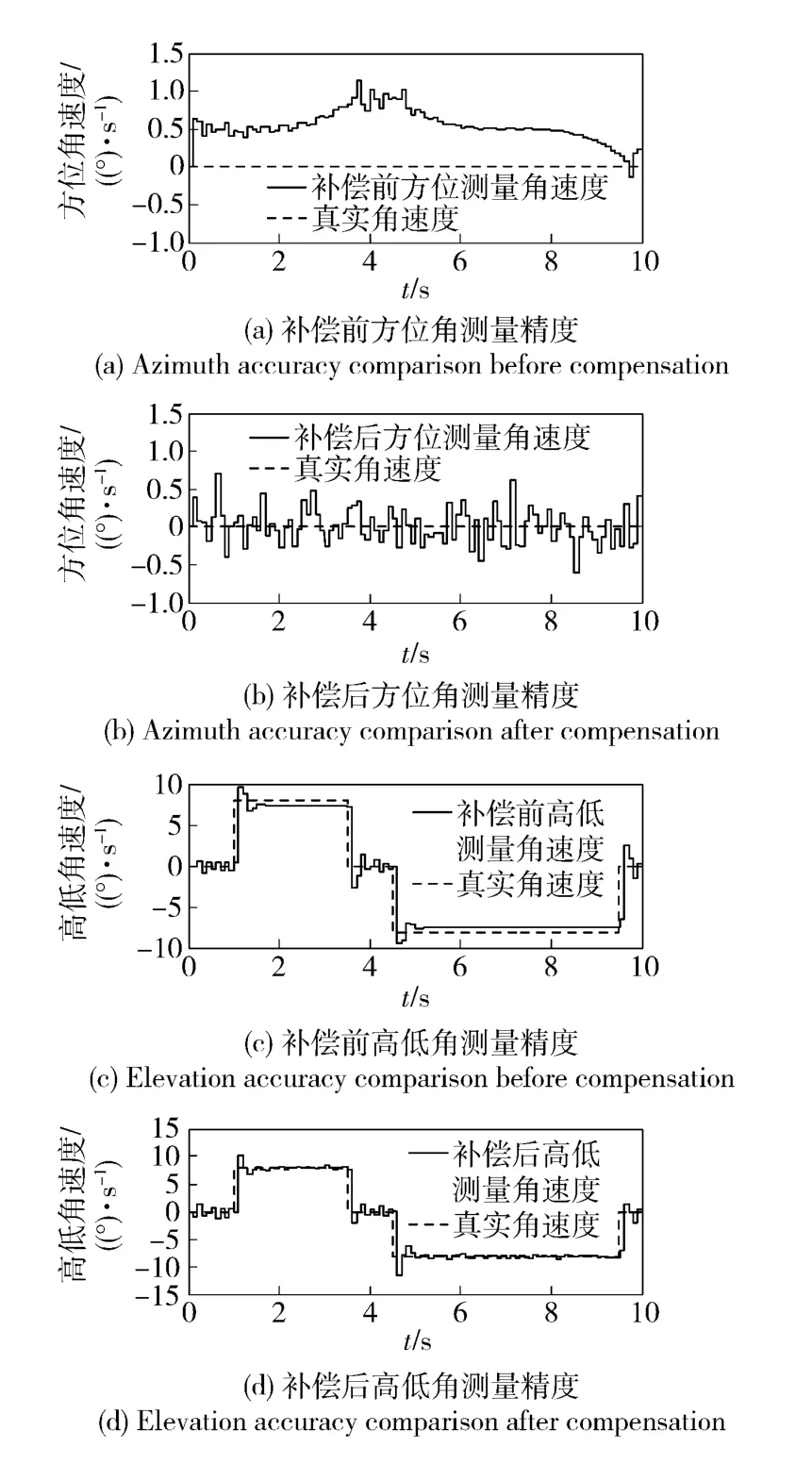
圖12 補償后導引頭的測量精度Fig.12 Seeker measurement accuracyies before and after compensation

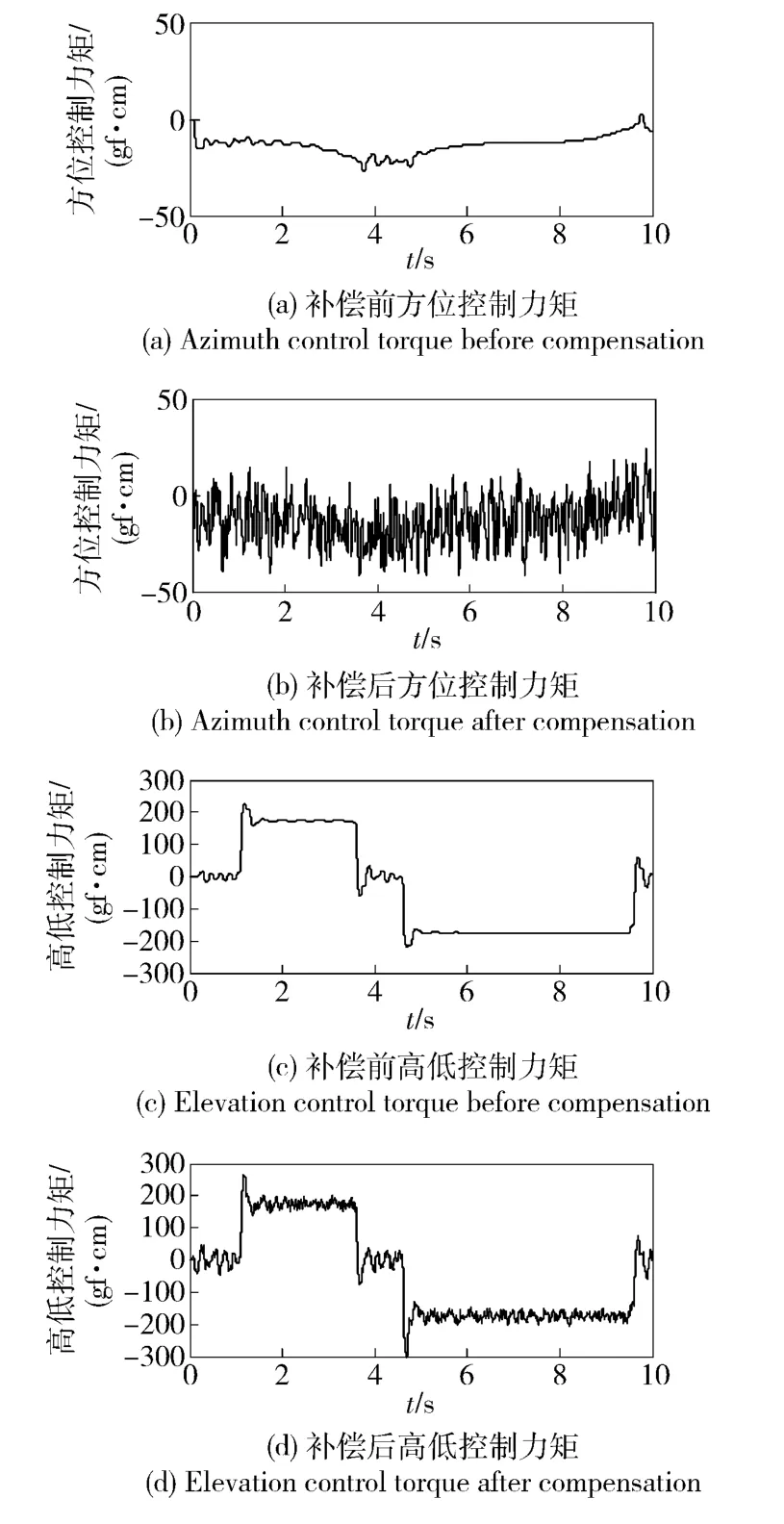
圖13 導引頭的控制力矩對比Fig.13 Comparison of seeker control torques

4 結論

以上的理論分析和仿真結果表明，考慮實際系統的多速率采樣問題，本文提出的由連續域奈奎斯特穩定性理論來指導設計導引頭DOB 采樣保持時間及濾波時間常數，能有效地幫助工程設計人員選取合適的參數。通過分析彈上可用信息，得到DOB所需的導引頭進動角速度信息可以直接由彈上測量信息獲得。利用DOB 對干擾力矩進行補償能有效提高導引頭的測量精度，減小導引頭隔離度。本文提出的方法對實際工程設計有參考意義，可以用來提高動力陀螺式導引頭的跟蹤測量精度。

References)

［1］陳佳實. 導彈制導與控制系統的分析與設計［M］. 北京:宇航出版社，1989:25 -47 CHEN Jia-shi. Analysis and design of missile guidance and control systems［M］. Beijing:China Astronautics Publishing House，1989:25 -47. (in Chinese)

［2］宋韜，林德福，王江. 平臺導引頭隔離度對導彈制導系統影響［J］. 哈爾濱工程大學學報，2013，34(10):1234 -1241.SONG Tao，LIN De-fu，WANG Jiang. Influence of seeker disturbance rejection rate on missile guidance system［J］. Journal of Harbin Engineering University，2013，34(10):1234 - 1241. (in Chinese)

［3］劉俊輝，單家元，劉永善. 動力陀螺式導引頭跟蹤能力分析［J］. 紅外與激光工程，2013，8(42):2209 -2215.LIU Jun-hui，SHAN Jia-yuan，LIU Yong-shan. Tracking performance of gyro-stabilized seeker［J］. Infrared and Laser Engineering，2013，8(42):2209 -2215. (in Chinese)

［4］Chun-Liang Lin，Yi-Hsing Hsiao. Adaptive feedforward control for disturbance torque rejection in seeker stabilizing loop［J］. IEEE Transactions on Control Systems Technology，2001，9(1):108 -121.

［5］Ohnishi K. A new servo method in mechatronics［J］. Trans Jpn Soc Elect Eng，1987(1):83 -86.

［6］Kempf C J，Kobayashi S. Disturbance observer and feedforward design for a high-speed direct-drive positioning table［J］. IEEE Transactions on Control Systems Technology，1999，7(5):513 -526.

［7］William F N，Zarchan P. Digital homing guidance-stability vs performance tradeoffs［J］. Journal of Guidance，Control，and Dynamics，1985，8(2):255 -261.

［8］單家元，孟秀云，丁艷，等. 半實物仿真［M］. 北京:國防工業出版社，2012:283 -286 SHAN Jia-yuan，MENG Xiu-yun，DING Yan，et al. Hardware in the loops［M］. Beijing:National Defense Industry Press，2012:283 -286. (in Chinese)

［9］于爽，付莊，趙言正，等. 基于干擾觀測器的慣性平臺摩擦補償方法［J］. 哈爾濱工業大學學報，2008，40(11):1820 -1833.YU Shuang，FU Zhuang，ZHAO Yan-zheng，et al. Method of friction compensation based on disturbance observer in inertial platform［J］. Journal of Harbin Institute of Technology，2008，40(11):20 -1833. (in Chinese)

［10］Takaji Umeno，Yoichi Hori. Robust speed control of DC servomotors using modern two degrees-of-freedom controller design［J］.IEEE Transactions on Industrial Electronics，1991，38(5):363 -367.