基于磁流變懸置的整車建模與振動控制的研究*

張自偉,鄭 玲,鄧召學,付江華,郭敏敏

(1.重慶大學，機械傳動國家重點實驗室，重慶 400030； 2.長安汽車研究院NVH研究所，重慶 401120)

前言

磁流變懸置是以磁流變液為載體構成的發(fā)動機隔振裝置，在外磁場作用下，磁流變液體黏度急劇變化，導致磁流變懸置阻尼力在一個較大范圍內改變[1]，磁流變懸置為實現(xiàn)發(fā)動機的有效寬頻隔振，提供了重要手段[2]。

由于磁流變懸置本身的高度非線性和滯回特性[3]，建立合理的磁流變懸置正、逆模型，是實現(xiàn)發(fā)動機磁流變懸置系統(tǒng)精確控制的前提條件[4]。參數(shù)化的Bingham模型簡單易于分析，能夠很好地表達力-位移特性，但不能描述磁流變阻尼器屈服前特征，即雙黏性特征、滯后特性和剪切變稀現(xiàn)象[5]。非參數(shù)化神經網絡[6]模型由于其良好的非線性逼近能力是最具應用前景的模型辨識方法之一。文獻[7]中利用遞歸神經網絡(RNN)對磁流變阻尼器建模，RNN網絡以內部狀態(tài)反饋來描述磁流變阻尼器的非線性特征，但因網絡結構復雜，存在訓練算法收斂速度慢的問題。

近年來，國內外的很多學者在發(fā)動機單自由度模型的基礎上，研究了基礎與發(fā)動機之間的隔振及其控制問題[8]，取得了較為豐富的研究成果。然而單自由度模型只適合研究單質量塊單方向的振動，為了研究發(fā)動機最主要的垂向-橫搖、垂向-橫向等振動，文獻[9]中研究了單層隔振系統(tǒng)放置于車身上的2自由度隔振模型及垂向隔振控制問題。長期以來，國內外學者在研究發(fā)動機自身振動時，往往把它模擬成一個6自由度的剛體，建立發(fā)動機整機振動的一般模型——6自由度模型，并以此為基礎來研究發(fā)動機的隔振和各種控制方法問題[10]，具有更普遍的意義。

目前，國內外學者對磁流變懸置的半主動控制也做了大量研究工作，文獻[11]中對實時阻尼調節(jié)做了較深入的研究，其關鍵是確定輸入信號(轉速信號)與輸出信號(磁流變懸置的勵磁電流)之間精確的數(shù)學關系式，從而起到最佳的控制效果。文獻[12]中以減小發(fā)動機對基座的垂向力為目標，設計了仿人思想修改參數(shù)的發(fā)動機垂向隔振模糊控制器。根據發(fā)動機激勵頻率和力傳遞率，通過建立的模糊規(guī)則可得到磁流變懸置需要的阻尼大小。文獻[13]中在磁流變懸置系統(tǒng)內設計了一個線性二次型高斯(LQG)控制器，實驗表明：結構的加速度振動水平和傳遞到機座的力能被有效減小。

本文中利用廣義回歸神經網絡(GRNN)，只須確定一個光滑因子參數(shù)，即可降低人為確定權值對逼近能力的影響，通過磁流變懸置的動態(tài)試驗數(shù)據建立GRNN正、逆模型；然后針對基于磁流變懸置的整車10自由度動力學系統(tǒng)，設計了模糊控制器，對發(fā)動機的垂向振動進行控制。仿真結果表明，該模糊控制器的設計合理有效，能很好地衰減發(fā)動機的振動，驗證了GRNN正、逆模型的正確性。

1 磁流變懸置結構設計和動態(tài)性能試驗

針對某汽車動力總成設計了基于周徑向流動模式的磁流變懸置結構，如圖1所示。懸置上部通過橡膠主簧、加強塊和連接螺栓與發(fā)動機連接，懸置下部通過下殼體法蘭盤上的通孔利用螺栓與車架連接，橡膠主簧和磁芯之間、磁芯和橡膠底膜之間分別形成上、下液室，液室充滿磁流變液體。內上磁芯和外上磁芯、下磁芯之間形成周向阻尼通道，內上磁芯和內磁芯、內磁芯與下磁芯之間形成徑向阻尼通道。在發(fā)動機動載荷作用下，發(fā)動機通過連接螺栓帶動加強塊和橡膠主簧上下運動，磁流變液體通過阻尼通道在上下液室之間流動。當勵磁電流改變時，阻尼通道內的磁感應強度也隨之改變，使阻尼通道中的磁流變液黏度發(fā)生變化，從而實現(xiàn)磁流變懸置輸出阻尼力無級連續(xù)可調。

采用MTS綜合試驗臺對自行設計的磁流變懸置進行動態(tài)性能測試，如圖2所示，試驗共采集了行程為0.2和1mm，頻率范圍為1～50Hz，頻率間隔為1Hz，電流為0、0.5、1.0和1.5A時的試驗數(shù)據，為磁流變懸置模型和控制算法的設計奠定基礎。

2 GRNN正逆模型

在上述GRNN模型上建立磁流變懸置辨識模型的步驟是：首先確定神經網絡的輸入輸出變量；然后處理原始訓練數(shù)據，即為消除各輸入變量因物理意義各異、數(shù)量級不同對其網格訓練的影響，在訓練網格之前對各輸入變量的數(shù)據進行歸一化處理；最后確定光滑因子σ。

2.1 GRNN正模型

利用磁流變懸置動態(tài)性能試驗數(shù)據，基于GRNN模型對磁流變懸置正模型進行辨識，其原理如圖4所示。選取前一時刻的位移xk-1、速度vk-1、電流Ik-1、恢復力Fk-1和當前時刻的激振頻率fk、位移xk、速度vk、電流Ik為輸入變量，當前時刻的恢復力Fk為輸出變量，其中N表示歸一化處理，D表示延遲單位采樣時間。

為定量評價GRNN正模型預測精度，建立評價指標[14]如下：

(1)

以激振頻率為15和25Hz，激振電流為0.5和1.0A為例進行說明，其試驗值與預測值如圖5所示，根據式(1)可計算出圖5中GRNN神經網絡的預測精度EF，如表1所示。

表1 相對預測精度EF

由表1可知，基于GRNN的非參數(shù)化磁流變懸置正模型能很好地預測其恢復力。

2.2 GRNN逆模型

同樣地，利用GRNN可建立其非參數(shù)化逆模型。其GRNN逆模型辨識原理如圖6所示，輸入變量分別為前一時刻的位移xk-1、速度vk-1、電流Ik-1、恢復力Fk-1和當前時刻的激振頻率fk、位移xk、速度vk、恢復力Fk，輸出變量為當前時刻的激勵電流Ik。其中N表示歸一化處理，D表示延遲單位采樣時間。

為定量評價GRNN逆模型預測精度，建立評價指標如下：

(2)

以激振頻率15Hz為例，經GRNN逆模型預測的激勵電流與試驗值如圖7所示。根據式(2)可計算出圖7中GRNN神經網絡的預測精度EI，見表2。

激勵條件00A05A10A15A預測精度EI00003569981%9957%9936%

由表2可知，基于GRNN的非參數(shù)化磁流變懸置逆模型能很好地預測其激勵電流。

綜上所述，基于GRNN的非參數(shù)化模型在磁流變懸置的正、逆模型辨識方面具有較高的辨識能力，為控制策略研究奠定了基礎。

3 磁流變懸置半主動控制

3.1 基于磁流變懸置的整車動力學模型

由于發(fā)動機往往處于復雜的整車工作環(huán)境中，為了體現(xiàn)發(fā)動機與車體間的振動傳遞關系，改善整車的NVH特性，把發(fā)動機隔振系統(tǒng)放在整車的振動模型中加以研究，往往更有實際意義。

建立如圖8所示的基于磁流變懸置的整車10自由度動力學模型，將車身視為剛體,考慮發(fā)動機的垂向、俯仰、側傾3個自由度的運動，車身的垂向、側傾、俯仰3個方向的運動，以及4個簧下質量的4個自由度運動。發(fā)動機由4點懸置支撐，其中1號為磁流變懸置，其他為被動橡膠懸置。發(fā)動機坐標系原點在發(fā)動機質心位置，x軸指向汽車前方，y軸指向汽車左側，z軸由右手定則確定。車身坐標系原點在車身質心處，坐標軸方向與發(fā)動機坐標系平行。

發(fā)動機動力學方程為

(3)

(4)

(5)

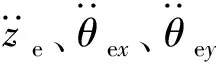
車身動力學方程為

(6)

leb2fe2+leb3fe3-leb4fe4+leb1u1

(7)

teb2fe2-teb3fe3-teb4fe4-teb1u1

(8)

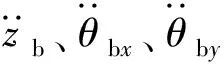
4個簧下質量垂向動力學方程為

(9)

(10)

(11)

(12)

式中：mui為簧下質量；kui為輪胎剛度；zui為簧下質量垂向位移，其中i=1～4。

對于傳統(tǒng)的被動懸架而言，其懸架力：

(13)

同理，其懸置力：

(14)

式中：kbi為懸架剛度；cbi為懸架阻尼；kei為懸置剛度；cei為懸置阻尼。

當車身俯仰角和側傾角較小時，懸架上端4個點的垂向位移與車身坐標原點位移的關系為

(15)

當發(fā)動機俯仰角和側傾角較小時，懸置上端4個點的垂向位移與發(fā)動機坐標原點位移的關系為

(16)

懸置下端4個點的垂向位移與車身坐標原點位移的關系為

(17)

令q=(zeθexθeyzbθbxθbyzu1zu2zu3zu4)T，U=(u10 0 0)T，F(xiàn)e=(FZFθxFθy)T，整理以上車輛運動方程，可得微分方程的標準形式：

(18)

式中：Mw為質量矩陣；Cw為阻尼矩陣；Kw為剛度矩陣；Bw為懸置可控阻尼力輸入矩陣；Dw為發(fā)動機激勵輸入矩陣。

(19)

Y=CX

(20)

建模過程中所用參數(shù)如表3所示。

3.2 模糊控制器設計

近年來由于模糊控制不需要被控對象的精確數(shù)學模型，控制靈活，魯棒性強，被越來越多地應用于復雜的非線性時變系統(tǒng)中，取得了良好的控制效果。圖9為磁流變懸置模糊控制示意圖。本文中設計了雙輸入單輸出的模糊控制器，以發(fā)動機2階主頻f和懸置點加速度a作為輸入，輸出量為磁流變懸置的可控阻尼力u。通過GRNN逆模型求得控制電流，再通過GRNN正模型求得實際控制阻尼力。

輸入量2階主頻變化范圍為[0 100]Hz，加速度變化范圍為[-20 20]m/s2，輸出阻尼力變化范圍為[-300 300]N。取輸入量2階主頻模糊集合初始論域為[0 8]，對應模糊子集為{PZPSPMPBPL}，輸入量加速度和輸出量可控阻尼力模糊集合初始論域為[-6 6]，對應模糊子集為{NBNMNSNZPZPSPMPB}。以經驗和理論推導，建立在“低頻時使振動位移盡快衰減為零和高頻時使振動速度盡快衰減為零”的控制原則，表4為模糊控制規(guī)則。

3.3 仿真試驗

利用Matlab仿真軟件，為某自主品牌車型建立基于磁流變懸置和被動懸置的整車仿真模型。仿真時，發(fā)動機采用單頻激勵方式，對轉速為400r/min的起動工況、750r/min的怠速工況和1 500r/min的穩(wěn)態(tài)工況時磁流變懸置1的上端加速度振動信號進行測量，并和被動與模糊控制策略進行對比，結果如圖10和圖11所示。

由圖可知，發(fā)動機轉速為400、750和1 500r/min時，與被動控制相比，模糊控制的振動加速度和加速度功率譜峰值均有顯著降低。

表5為懸置1點加速度均方根值。由表5可知，轉速為400、750和1 500r/min時，懸置點處速度均方根值分別下降58.51%、37.63%和22.75%，下降非常顯著，說明模糊控制器的設計合理有效，很好地衰減了發(fā)動機的振動。

4 結論

(1) 基于磁流變懸置動態(tài)性能試驗數(shù)據和GRNN辨識方法建立了磁流變懸置的正、逆模型。由辨識結果可知，GRNN具有非常高的辨識精度，適用于磁流變懸置力學模型辨識，具有較好的應用前景。

(2) 在GRNN正、逆模型的基礎上，建立了基于磁流變懸置的整車10自由度動力學模型，設計了垂向模糊控制器。仿真結果表明，在寬頻范圍內，很好地衰減了發(fā)動機的振動，特別是在發(fā)動機轉速對應的2階主頻處，控制后懸置點的振動加速度幅值下降顯著；該模糊控制器的設計是合理有效的。

[1] Koo J H, Goncalves F D, Ahmadian M. A Comprehensive Analysis of the Response Time of MR Dampers[J]. Smart Materials and Structures,2006,15(2):351-358.

[2] Carlson J D. Magnetorheological Fluid Actuators. Adaptronics and Smart Structures[M]. Edited by Jendritza DJ and Janocha H, Springer Verlag,1997.

[3] Heinonen J. Preliminary Study of Modelling Dynamic Properties of Magnetorheological Fluid Damper[R]. VTT Technical Research Centre of Finland. ESPOO,2006.

[4] Boada M J L, Calvo J A. Modeling of a Magnetorheological Damper by Recursive Lazy Learning[J]. International Journal of Non-Linear Mechanics 2011,46:479-485.

[5] Gamato D, Filisko F E. High Frequency Dynamic Mechanical Study of an Aluminosilicate Electrorheological Material[J].Journal of Rheology,1991,35:1411-1425.

[6] Du H, Lam J, Zhang N. Modelling of a Magneto-rheological Damper by Evolving Radial Basis Function Networks[J]. Engineering Applications of Artificial Intelligence,2006,19(8):869-881.

[7] Wang D H, Liao W H. Neural Network Modeling and Controllers for Magnetorheological Fluid Dampers[C]. The 10th IEEE International Conference on Fuzzy Systems,2001,3:1323-1326.

[8] Yu Y H, Naganathan N G, Dukkipati R V. A Literature Review of Automotive Vehicle Engine Mounting Systems[J]. Mechanism and Machine Theory,2001,36:123-142.

[9] Yang J M, Suematsu Y, Kang Z. Two-Degree-of-Freedom Controller to Reduce the Vibration of Vehicle Engine-Body System[J]. IEEE Transactions on Control System Technology,2001,9(2):295-304.

[10] 張紅靈.振動主動控制若干問題的研究[D].安徽:中國科技大學,2007.

[11] 魏付俊.汽車動力總成磁流變懸置的設計和半主動控制研究[D].南京:南京航空航天大學,2007.

[12] 李銳.發(fā)動機磁流變懸置隔振模糊控制與仿真[J].系統(tǒng)仿真學報,2009,21(4):944-947.

[13] Hong S R, Choi S B. Vibration Control of a Structural System Using Magneto-Rheological Fluid Mount[J]. Journal of Intelligent Material Systems and Structures,2005,16(11-12):931-936.

[14] 王昊,胡海巖.磁流變阻尼器的模糊逼近[J].振動工程學報,2006,19(1):31-36.