步槍彈侵徹明膠的表面受力模型

莫根林，吳志林，馮杰，劉坤

(南京理工大學 機械工程學院，江蘇 南京210094)

0 引言

彈道明膠被廣泛地用作人體組織的替代物，用于人體創傷的評估。它具有透明性質，利用高速攝影可以方便地獲得彈頭在其中的位置和方向信息。實驗表明步槍彈在明膠中的翻滾角度能夠大于90°，此時小攻角條件下的彈道方程不再適用，需要建立能夠描述彈頭在大攻角條件下運動的彈道模型［1］。

文獻［2］中:假設彈頭阻力和速度呈正比，建立了彈頭的水平運動方程;假設彈頭豎直方向的受力和彈頭的轉矩僅和彈頭的攻角有關，建立了彈頭的豎直運動方程和繞質心的轉動方程;根據實驗數據擬合得到了阻力系數和攻角的關系。Weinacht 等［3］在文獻［2］的基礎上獲得了彈頭在任意起始攻角下轉動方程的解析解。Peters 等［4］采用修正的伯努利方程建立了彈頭質心的水平運動方程，在彈頭的平面轉動方程中引入了動力矩系數和靜力矩系數，建立了力矩系數和彈頭外形的聯系。文獻［5 -6］假設彈頭質心的速度方向水平不變、阻力系數CD和法向力系數CN為偏角φ 的函數，利用實驗數據對模型假設進行了驗證;劉坤等［7］在彈頭的平面彈道模型中區分了攻角和偏角的概念，從而平面模型中考慮了彈頭豎直方向的運動。上述建立的模型均為平面彈道模型，沒有考慮彈頭的運動平面和拍攝平面的關系，也沒有考慮彈頭轉動對侵徹過程的影響。

為了獲得彈頭運動規律，首先需要確定彈頭的受力。在靶板的侵徹動力學中，彈頭表面和侵徹介質的相互作用力通常用彈頭的幾何尺寸和動力學參數表示［8］。將接觸應力表達為微元速度和靶標強度的方法分別在鋁板、混凝土靶、巖石靶和鋼板的侵徹實驗中得到了有效驗證［9-11］。本文將侵徹明膠彈頭表面的微元應力表達為微元速度和明膠強度的函數，通過步槍彈侵徹明膠的實驗，對該模型進行間接驗證。

1 模型

1.1 現象描述

現有步槍彈彈頭侵徹明膠過程中會發生失穩翻滾，步槍彈在30 cm 明膠塊中的位置和姿態變化示意圖如圖1所示。

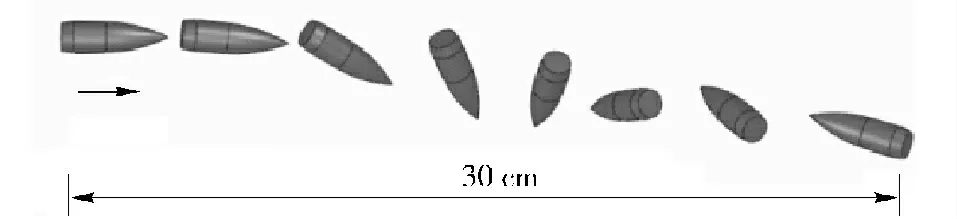
圖1 彈頭在明膠中的運動過程Fig.1 Penetration process of rifle bullet in gelatin

從圖中可以看出，彈頭侵徹過程中質心在水平方向和豎直方向均有位移變化，彈頭姿態的變化是空間的而不是平面的，彈頭攻角能夠達到幾十度。為了描述彈頭在明膠中的空間運動，必須確定彈頭任意時刻受到的合力和合力矩。

1.2 模型假設

為簡化模型，提出如下假設:

1)彈頭為剛性體，不考慮彈頭侵徹過程中的彈塑性變形;

2)彈頭為旋轉體，不考慮其表面劃痕等因素的影響;

3)彈頭在明膠中的運動時間一般小于1 ms，所以不考慮重力影響;

4)根據文獻［9 -11］，假設微元面侵徹明膠時的受力為F，可以表示為

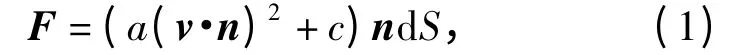
式中:a、c 為力學系數;v 為面元的速度;dS 表示面元的面積;n 為面元的外法線方向。

1.3 幾何和動力學參數

旋轉體彈頭可以看作是一條曲線繞中心線旋轉形成的實體。由于曲線可以近似看為微小直線段的組合，因此彈頭表面可以看作是很多圓錐面的組合，對彈頭表面的受力分析可以簡化為對錐面的受力分析。

為了分析錐面上任意位置微元的受力。建立慣性坐標系O'x'y'z'和連體坐標系Oxyz，如圖2所示。令O'x'y'z'的基矢量為i'、j'和k'，Oxyz 的基矢量為i、j 和k.采用歐拉角描述連體坐標系相對慣性坐標系的轉動，其中φ、ψ 和θ 分別為自轉角、進動角和章動角。θ 為Oz 軸與O'z'的夾角，原點O 位于彈頭的質心位置，Oz 與彈頭的對稱軸重合。zt和zb分別為微元頂面和底面的z 坐標，R2和R1分別為微元頂面和底面圓面的半徑。錐面上任意z 位置處A 點速度為

式中:vc為質心運動速度;ω 為彈頭轉動角速度;rA為A 點相對矢徑。

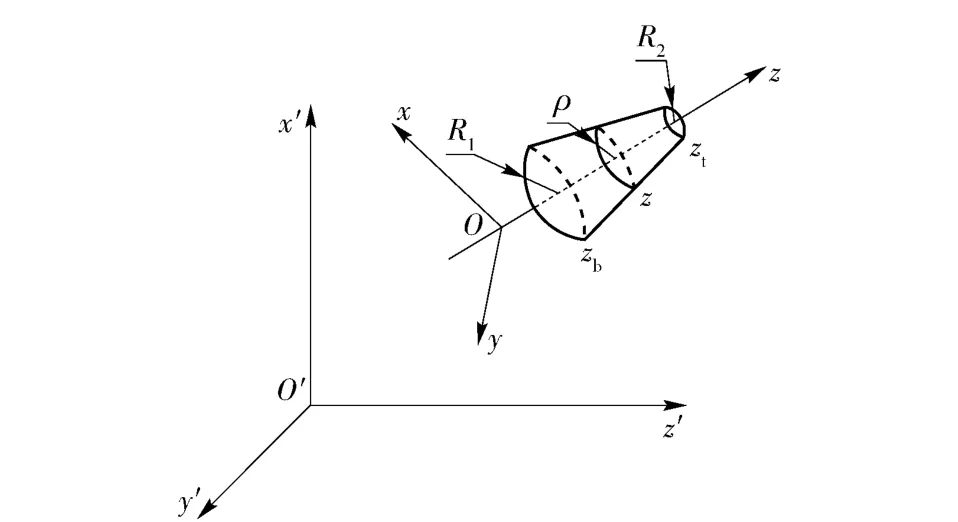
圖2 錐面和連體坐標系Oxyz 與固定坐標系O'x'y'z'關系Fig.2 Schematic of a frustum of a cone with body coordinate system Oxyz in fixed coordinate system O'x'y'z'

轉動角速度ω 可以表示為

式中:ωx、ωy和ωz為角速度在x、y 和z 方向的分量，表達式為

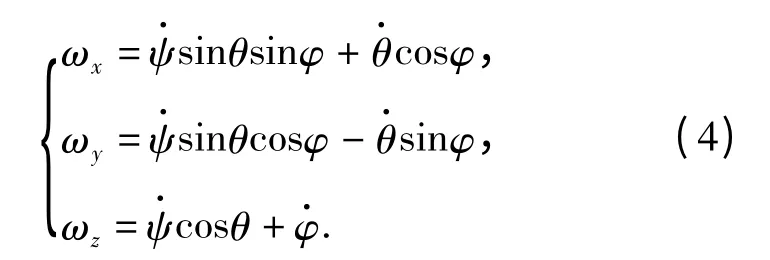
矢徑r'A可表示為

式中:r'c為彈頭質心的矢徑;rA可以表示為

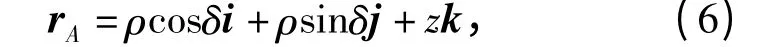
ρ 和δ 分別為rA在Oxy 平面的投影向量的模和投影向量與x 軸的夾角。

采用坐標z 和δ 表示微元的面積dS，可得

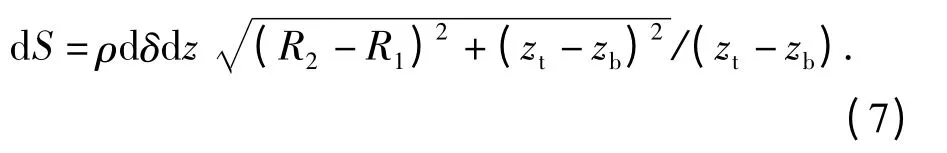
A 點的外法線方向n 可以表示為

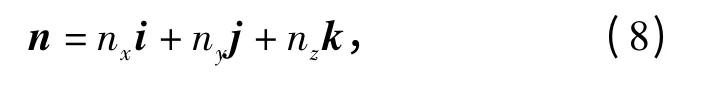
式中:

將(2)式～(9)式帶入(1)式即可求得任意位置點出的受力F.將F 對質心O 點取矩得

1.4 運動方程

根據高等動力學理論［12］，彈頭的質心運動方程可以表示為

式中:m 表示彈頭質量;x'c、y'c和z'c表示彈頭質心在固定坐標系中的坐標;∑Fx'、∑Fy'和∑Fz'為彈頭在i'、j'和k'方向所受的合力。

彈頭的歐拉運動方程可以表示為

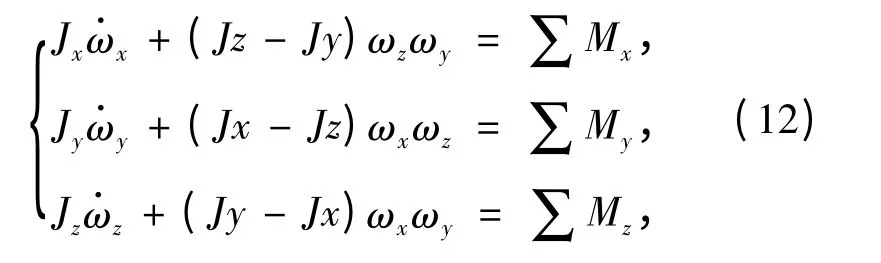
式中:Jx、Jy和Jz分別為彈頭繞x 軸、y 軸和z 軸的轉動慣量;∑Mx、∑My和∑Mz為彈頭繞x 軸、y軸和z 軸的力矩分量。

對(4)式、(11)式和(12)式整理可得x'c、y'c、z'c、φ、ψ 和θ 表示的剛體的空間方程為

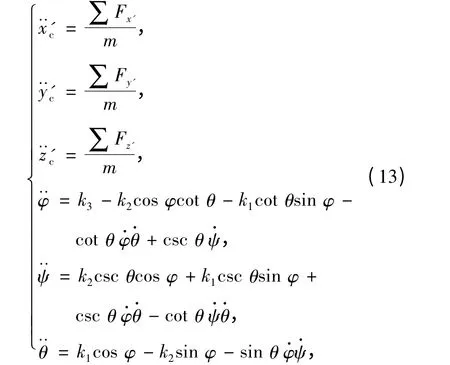
式中:k1、k2和k3分別為

利用數值積分，將(1)式和(10)式得到的∑Fx'、∑Fy'、∑Fz'、∑Mx、∑My和∑Mz帶入(13)式和(14)式。在初始條件已知的情況下，通過4 階龍格-庫塔法即可得到彈頭位置和姿態的變化規律。

2 實驗驗證

實驗中選用10%的彈道明膠，明膠塊尺寸為30 cm×30 cm×30 cm，明膠塊在使用前在4 ℃保溫箱中保溫24 h.彈道槍距離明膠塊50 m 發射7.62 mm步槍彈侵徹明膠塊，通過光電靶測量明膠前1 m 處彈頭速度，采用1.5 MHz 幀頻的高速攝影從側面拍攝彈頭在明膠中的運動姿態。圖3為高速攝影和明膠塊在固定坐標系中相對位置示意圖。圖4為彈頭在明膠出口位置的實驗圖像，可以看出彈頭在出口時幾乎沒有塑性變形，因此可以將侵徹過程中的彈頭看作剛性體。

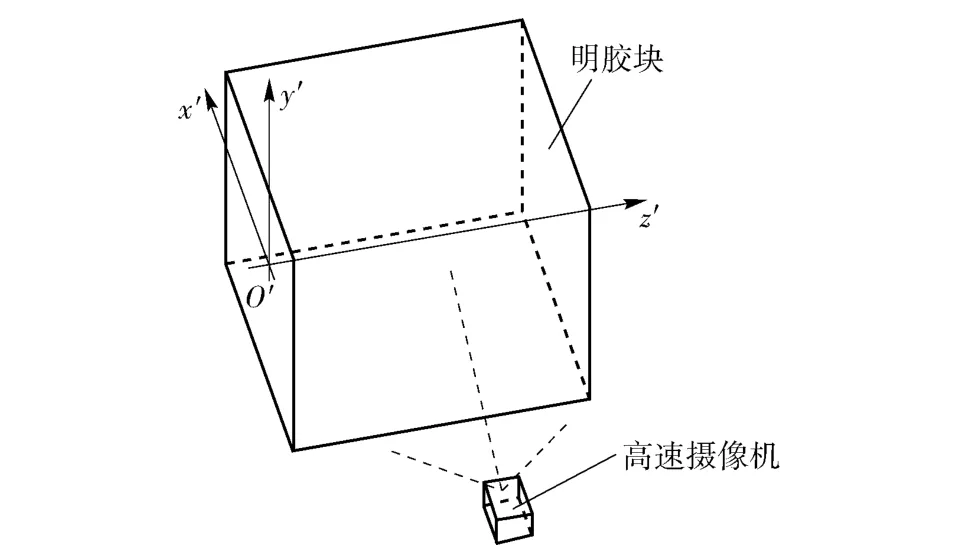
圖3 高速攝像機和明膠塊在固定坐標系O'x'y'z'中的位置Fig.3 Positions of the high-speed camera and gelatin block in O'x'y'z'

圖4 明膠塊出口處的7.62 mm 彈頭Fig.4 7.62 mm bullet at exit of the gelatin block

模型中的初始參數如表1和表2所示，下標“0”表示相應物理量的初始值，其中彈頭的角速度分量通過理論計算得到［13］。由于高速攝影獲得的平面圖像無法確定三維空間的歐拉角，所以初始歐拉角由試算得到。實驗表明空氣中彈頭歐拉角的取值必須保證彈頭的攻角比較小［13-14］，因此彈頭侵徹明膠的初始歐拉角必須是一個較小值。根據表1和表2可以得到彈頭攻角為3.5°，可以認為給定的初始值是合理的。明膠的力學參數根據鋼球侵徹明膠的實驗數據擬合得到［15］。

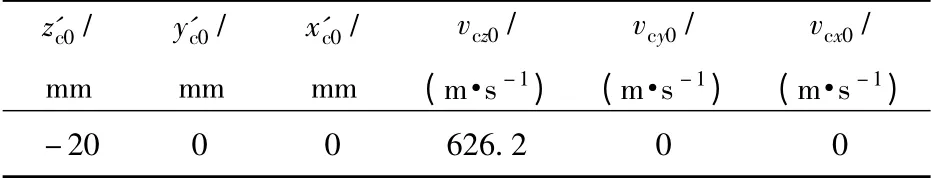
表1 7.62 mm 彈頭的初始位移和速度分量Tab.1 Initial displacements and initial velocity components of 7.62 mm projectile

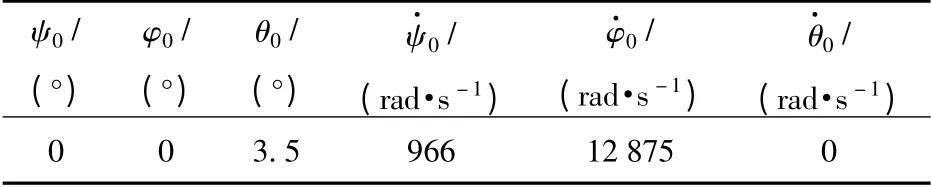
表2 7.62 mm 彈頭的初始歐拉角和初始角速度Tab.2 Initial Eulerian angles and initial angular velocities of 7.62 mm projectile

理論計算結果和實驗值的比較如圖5～圖7所示。圖5為彈頭質心z＇c坐標隨時間的變化，最大實驗誤差7.8 mm，平均實驗誤差3.1 mm;圖6為y＇c隨z＇c的變化，最大實驗誤差2.3 mm，平均誤差2.1 mm;圖7為彈頭在O'y'z'平面投影轉角隨z＇c坐標的變化，最大實驗誤差8.9°，平均誤差2.3°.可見，實驗值和理論值之間的誤差較小。

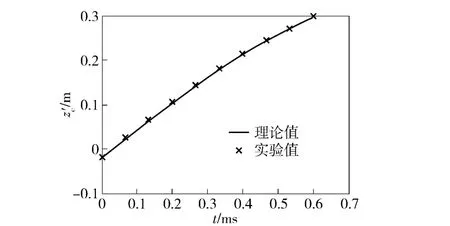
圖5 z＇c與t 的關系Fig.5 z＇c vs.t

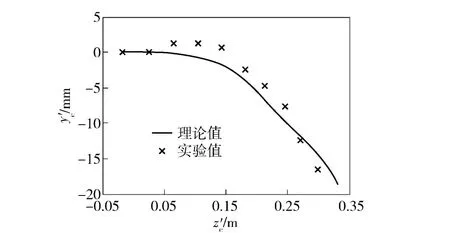
圖6 y'c與z＇c的關系Fig.6 y＇c vs.z＇c

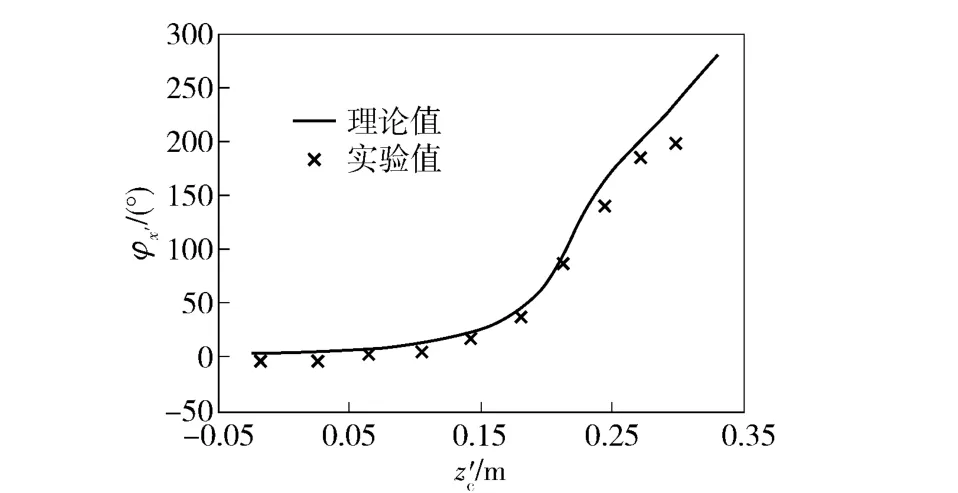
圖7 O'y'z'平面投影轉角φx'與z＇c的關系Fig.7 Projection angle φx' vs.z＇c on O'y'z'

3 討論分析

3.1 章動角和平面投影轉角

理論計算得到的彈頭章動角θ 和彈頭在O'y'z'平面投影轉角φx'的關系如圖8所示。它們的關系可表示為

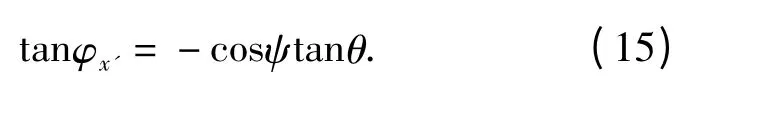
彈頭的平面運動模型中，若假設彈頭在高速攝影拍攝平面內運動［4-7］，此時其進動角為0°，從(15)式可知，θ 和φx'的大小相同;在空間運動中，當進動角變化或不為0°時，θ 和φx'將有很大的不同。因此平面模型的實驗驗證需要確定彈頭的運動平面。

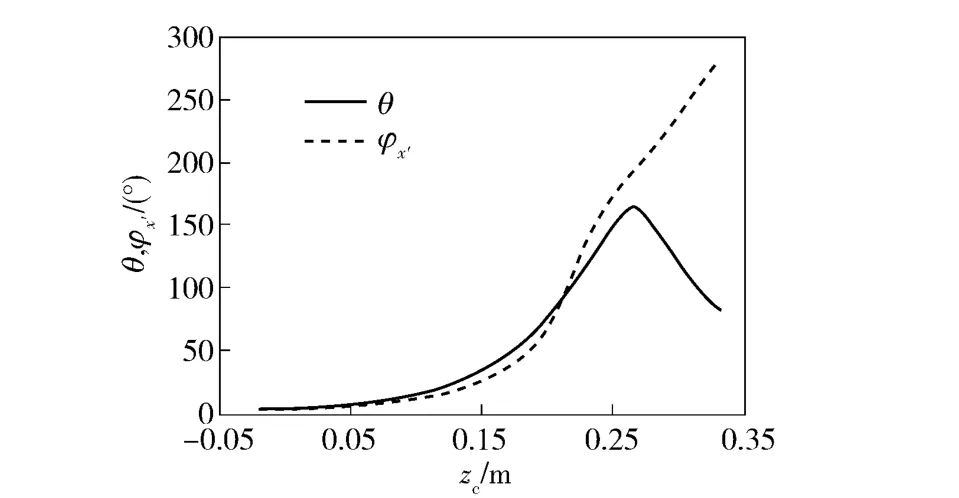
圖8 投影角φx'和θ 的比較Fig.8 Comparison between φx' and θ

彈頭外形在彈尖和彈尾處變化比較劇烈，與該處接觸的明膠必然處于應力集中狀態。明膠在軸對稱膨脹過程中，該處也就較容易產生徑向裂紋。顯然裂紋方向的變化是由彈頭的進動角變化引起的，所以彈頭在明膠中進動角的變化可以從明膠中的裂紋方向看出。圖9為第2 節中7.62 mm 彈頭進動角(理論值)隨侵徹距離的變化。圖10為明膠中裂紋方向變化形成的裂紋曲面，和圖9中的曲線變化相似，明膠中的裂紋方向在0.25 m 前基本不變，在0.25 m 后發生劇烈變化。圖10進一步表明了模型假設的合理性。

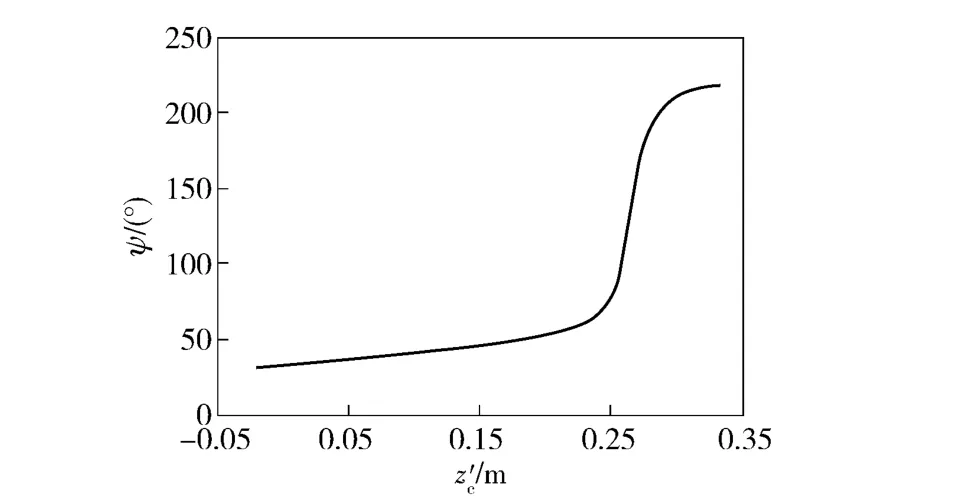
圖9 進動角隨z＇c的變化Fig.9 ψ vs.z＇c

3.2 力學系數a 和c

圖10 明膠中的裂紋曲面Fig.10 Curved surface of cracks in gelatin block

明膠是一種應變率相關材料。Kwon 等［16］利用單軸壓縮實驗獲得了10%明膠應變率在2 000 ～3 200 s-1之間時，應力與應變的實驗數據;Cronin 等［17］通過單軸壓縮實驗得到了應變率為0.01 s-1、10 s-1、117 s-1和1 552 s-1時，應力與應變的實驗數據;Moy 等［18］采用拉伸實驗得到了應變率為0.001 s-1、0.01 s-1和1 s-1時，應力與應變的實驗數據。上述實驗均表明明膠的力學性質與應變率具有較大相關性。對于明膠的本構模型，文獻［19 -20］建立了準靜態條件下的明膠超彈性本構模型和粘彈性固體模型。

Shepherd 等［21］通過實驗獲得了沖擊速度75 ～860 m/s 時，20% 明膠的雨貢紐曲線。文獻［16 -21］中的實驗數據是在明膠不存在剪切破壞的條件下獲得的。在破片侵徹實驗中可以觀察到彈道周圍的明膠存在明顯的剪切破壞，這種破壞對侵徹過程的影響程度尚不清楚。因此不能直接從上述文獻中得到10%明膠的力學參數a 和c.

Mo 等［15］采用本文的面元積分方法，對直徑3 mm、4 mm 和4.8 mm 球形破片侵徹明膠的實驗數據進行了擬合，間接確定了模型中的力學系數。本文力學系數a 和c 的取值與文獻［15］相同。實驗中破片撞擊速度在600 ～800 m/s 范圍。對于低速100 ～300 m/s 情況下，明膠的力學系數是否保持不變;明膠力學系數是否和破片外形的關系都有待進一步研究。將在實驗中增加對柱形和菱形破片的侵徹研究，并采用不同發射速度研究速度對力學系數的影響。

4 結論

本文在彈頭表面受力模型的基礎上，分析了旋轉體彈頭的受力，運用4 階龍格-庫塔法通過求解剛體的空間運動方程，得到了7.62 mm 步槍彈侵徹明膠過程的質心位置、空間姿態變化規律。理論計算值和實驗值誤差較小，從而間接證明了表面受力模型的合理性。模型中力學系數是從球形破片侵徹明膠的實驗中間接得到的，它們隨沖擊速度、破片外形的影響有待進一步研究。

References)

［1］ Kneubuehl B P，Coupland R M，Rothschild M A，et al.Wound ballistics:basics and applications［M］.Berlin:Springer，2011:95 -100.

［2］ Roecker E T.On yawing motion，velocity decay and path deflection of projectile penetrating cavitating media，ADA168220［R］.Maryland:US Army Ballistic Research Laboratory Aberdeen Proving Ground，1986.

［3］ Weinacht P，Cooper G R.Analytical solutions for the linear and nonlinear yawing motion in dense media［C］∥23rd International Symposiumon Ballistics.Tarragona， Spain: PAP Congresos，2007:1339 -1346.

［4］ Peters C E，Sebourn C L，Crowder H L.Wound ballistics of unstable projectiles.part I:projectile yaw growth and retardation［J］.Journal of Trauma，1996，40(3S):10S-15S.

［5］ Kneubuehl B，Sellier K.Woundballistics:a new understanding of the behavior of a bullet in a dense medium［C］∥Proceedings 13th International Symposium of Ballistics.Stockholm:IBC，1992:445 - 462.

［6］ Sellier K，Kneubuehl B P.Woundballlistics and the scientific background［M］.New York:Elsevier，1994:154 -168.

［7］ 劉坤，吳志林，徐萬和，等.彈頭侵徹明膠的運動模型［J］.爆炸與沖擊，2012，32(6):616 -622.LIU Kun，WU Zhi-lin，XU Wan-he，et al.A motion model for bullet penetrating gelatin［J］.Explosion and Shock Waves，2012，32(6):616 -622.(in Chinese)

［8］ Ben-Dor G，Dubinsky A，Elperin T.Ballistic impact:recent advances in analytical modeling of plate penetration dynamics-a review［J］.Applied Mechanics Reviews，2005，58(6):355-371.

［9］ Warren T L，Tabbara M R.Spherical cavity-expansion forcing function in PRONTO 3D for application to penetration problems，SAND-97-1174［R］.Albuquerque，NM:Sandia National Lab，1997.

［10］ Warren T L.Simulations of the penetration of limestone targets by ogive-nose 4340 steel projectiles［J］.International Journal of Impact Engineering，2002，27(5):475 -496.

［11］ Satapathy S，Bless S.Response of long rods to moving lateral pressure pulse:numerical evaluation in DYNA3D［J］.International Journal of Impact Engineering，2001，26(1):663 -674.

［12］ 張延教.高等動力學［M］.南京:華東工程學院，1984:56 -280.ZHANG Yan-jiao.Advanced dynamics［M］.Nanjing:East China Institute of Engineering，1984:56 -280.(in Chinese)

［13］ 高乃同.自動武器彈藥學［M］.北京:國防工業出版社，1990:334 -336.GAO Nai-tong.Automatic weapons and ammunition［M］.Beijing:National Defense Industry Press，1990:334 -336.(in Chinese)

［14］ Knudsen P J T，S?rensen O H.The initial yaw of some commonly encountered military rifle bullets［J］.Int J Legal Med，1994，107(3):141 -146.

［15］ Mo G L，Wu Z L，Liu K.Drag force analysis of spheres penetrating gelatin based on surface integral［J］.Applied Mechanics and Materials，2012，105:561 -565.

［16］ Kwon J，Subhash G.Compressive strain rate sensitivity of ballistic gelatin［J］.Journal of Biomechanics，2010，43(3):420 -425.

［17］ Cronin D S，Falzon C.Dynamic characterization and simulation of ballistic gelatin［C］∥2009 SEM Conference ＆ Exposition on Experimental ＆ Applied Mechanics.Albuquerque，NM:SEM，2009:1 -4.

［18］ Moy P，Tusit W T，Gunnarsson C L.Tensile deformation of ballistic gelatin as a function of loading rate［C］∥Proceedings of the 6th International Congress and Exposition.Orlando，FL:SEM，2008:2 -5.

［19］ Ottone M L，Deiber J A.Modeling the rheology of gelatin gels for finite deformations.part 1.elastic rheological model［J］.Polymer，2005，46(13):4928 -4937.

［20］ Ottone M L，Peirotti M B，Deiber J A.Modeling the rheology of gelatin gels for finite deformations.part 2.viscoelastic solid model［J］.Polymer，2005，46(13):4938 -4949.

［21］ Shephert C J，Appleby-Thomas G J，Hazell P J，et al.The dynamic behavior of ballistic gelatin［J］.AIP Conference Proceedings，2009，1195:1399 -1402.