電力系統最優潮流新模型及其內點法實現

聶永輝，肖 白，劉鳳蘭

（1.東北電力大學教務處，吉林132012；2.東北電力大學電氣工程學院，吉林132012；3.吉林市實驗中學，吉林132010）

最優潮流OPF（optimal power flow）問題是通過利用電力系統中可調節的控制手段，在滿足電力系統安全運行和物理約束條件限制下，使某種預定目標達到最優的系統穩定運行狀態。它是典型帶有連續變量和離散變量的大規模、非線性、非凸的規劃問題[1-2].從20 世紀60年代法國Carpentier提出最優潮流這個概念后，很多方法如線性規劃法、二次規劃法、簡約梯度法、牛頓法和智能方法等[3-4]，被用來解決復雜的優化問題，這些方法在某些方面存在明顯的缺陷，或不等式約束的處理問題，或最優解附近收斂性問題，或數值穩定性問題，制約了OPF 的求解范圍。

近年來，預測-校正原對偶內點法PCPDIPM（predictor-correctorprimal-dualinteriorpointmethod）被成功地應用于求解各種優化問題，因其具有良好的數值穩定性和快速收斂的特性被認為是解決大規模OPF 問題較有效的方法[5-11]。該算法主要是海森矩陣的形成和矩陣分解，約占了全部計算量的80%～90%，而現有的最優潮流模型是優化變量的高階函數，導致其海森矩陣不是定常矩陣，隨著迭代過程而變化，需要在迭代過程中不斷進行更新計算，為此增加了計算機消耗總時間。文獻[3]利用多中心柱正內點法的思想，通過關鍵參數的改進得至更大迭代步長，加速了算法整個收斂過程；文獻[5]利用最小度法MD（minimum degree）對修正方程系數矩陣進行節點優化排序，有效地減少了在三角分解過程中注入元產生的個數，以提高優化速度；文獻[9]根據電力系統拓撲結構的特點，通過重新排列原對偶變量在高度稀疏的修正方程系數矩陣中的順序，有效地減少了在三角分解過程中注入元產生的個數，從而降低計算機優化時間。

本文在有載調壓變壓器支路模型中增加虛擬節點，有載調壓變壓器支路功率方程用該節點的電壓來表達，使其不含有變壓器變比這個變量，從而在直角坐標系中建立了最優潮流問題的二次新模型，使得該模型有恒常的海森矩陣，在優化過程中也只需要一次計算，這樣縮短了內點法的計算總時間。為了進一步提高優化速度，利用列近似最小度法對內點法牛頓方程的系數矩陣進行節點優化排序，以進一步減少三角分解時注入元的產生。但由于虛擬節點的引入，增加了等式約束和優化變量的個數，從而增加了求解修正方程的時間，但增加的時間比形成修正方程時縮短的時間少，從而提高了計算速度。

1 最優潮流新模型

經典的有載調壓變壓器LTC（load tag changing tramsformer）支路模型，由理想變壓器和導納支路串聯組成，如圖1 所示。圖中：i 和j 分別為有載調壓變壓器的標準側節點和非標準側節點，t 為LTC變比，yt=gt+jbt為LTC 導納，=ei+jfi和=ej+jfj為LTC 各側節點電壓=PTij+jQTij和PTji+jQTji為標準側和非標準側節點注入功率。

則有載調壓變壓器支路功率方程為

圖1 有載調壓變壓器等效模型Fig.1 LTC equivalent model

由于LTC 變比的存在，導致有載調壓變壓器支路功率方程均是電壓和變比的高次函數，其對應的海森矩陣不是常數，因此在基于預測-校正原對偶內點的優化計算中，每次迭代都需要計算，增加了整個優化時間。為使式（1）～式（4）變成二次函數，本文在理想變壓器和串聯導納之間增加一個虛擬節點，其電壓為em+jfm，見圖1，S˙Tmj=PTmj+jQTmj是虛擬節點m 流向標準側節點j 的功率，S˙Tjm=PTjm+ jQTjm是低壓側節點j 流向虛擬節點m 的功率，則有載調壓變壓器支路功率方程變為

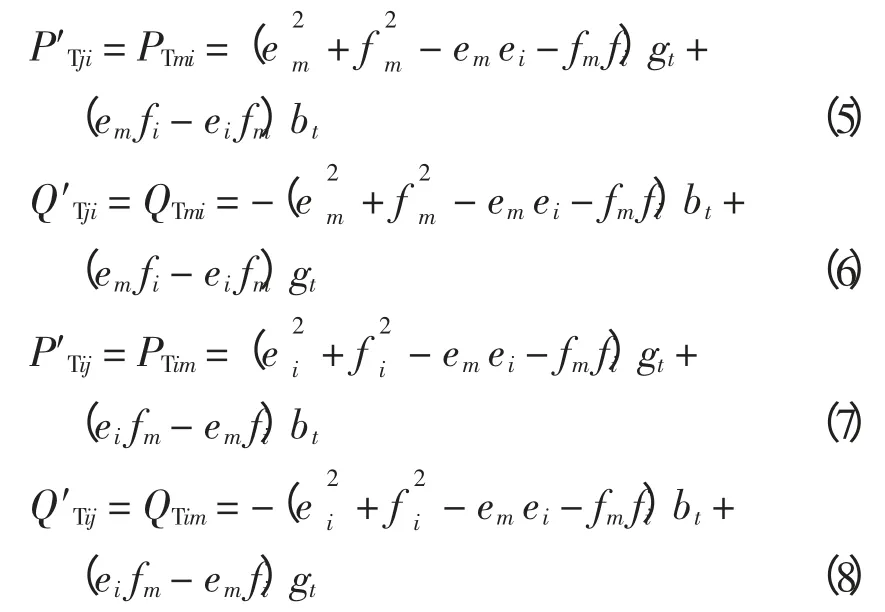
理想變壓器是無損的，其兩側電壓應滿足的關系為

引入以上變壓器模型，以各個節點的電壓實部與虛部、LTC 變比、發電機有功發電出力、無功發電出力及無功補償點無功出力為優化變量，在直角坐標下建立了二階最優潮流優化模型。

1）目標函數

以系統運行成本最小為目標函數的數學模型為

式中：PGi為第i 臺發電機的有功發電出力；c0i、c1i、c2i為其耗量特性曲線參數。

2）等式約束

等式約束包括節點功率平衡方程和電壓轉換方程，節點功率平衡方程為

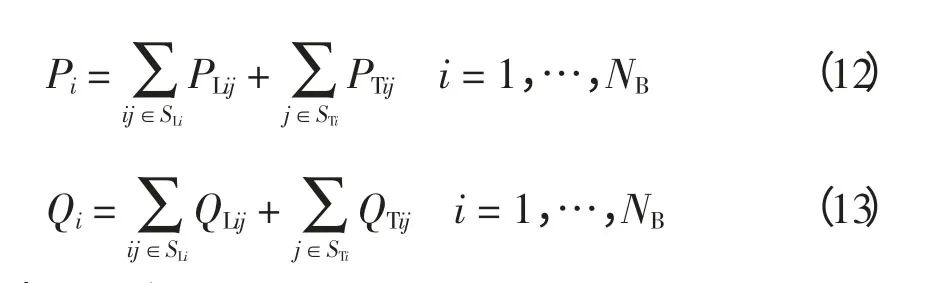
式中：PLij和QLij分別為常規線路及無載調壓變壓器支路的有功和無功；Pi和Qi分別為節點的有功注入和無功注入；PTij和QTij分別為有載調壓變壓器支路的有功功率和無功功率，如果節點i 為非標準側，則按式（5）和式（6）計算；如果節點i 為標準側，則按式（7）和式（8）計算；NB為系統原有的節點數，不包括虛擬節點；SLi為與節點i 相連的常規支路集合；STi為與節點i 相連的有載調壓變壓器支路集合。

（3）不等式約束

不等式約束包括節點電壓幅值、發電機有功發電出力和無功發電出力、并聯無功補償出力、LTC 變比的上下限約束和支路傳輸功率約束，即

式中，[]min、[]max為相應變量的下限和上限。

由于虛擬節點的引入，該最優潮流模型的目標函數、等式約束限制、不等式約束限制均是優化變量的二次函數。因此，各個函數的海森矩陣都是常數矩陣，在內點法的整個優化過程中只計算一次，不需要每次迭代都進行計算，優化計算的總時間大大降低[1-6]。

2 算例仿真

本文是在奔騰雙核（2G 內存）和操作系統為WINDOWS XP 的環境下，利用Matlab7 對IEEEl4、IEEE30、IEEE57、IEEE118、IEEE300 等節點系統建立新模型（Mod1）和常規模型（Mod2）進行仿真驗證，采用標幺值進行優化計算。表1 介紹了測試系統的基本情況，表中：n 代表系統節點數量，l 為系統支路數量，k 為系統變壓器支路數量，g 為系統發電機數量，r 為系統補償裝置數量，m1為等式約束個數，r1為不等式約束的個數，n1為修正方程的階數。由表1 可以看出，針對同一節點系統，有相同個數的不等式約束限制，但在等式約束限制的個數和修正方程的階數方面，所提模型比常規模型高。

表1 測試系統介紹Tab.1 Introduction of test systems p.u.

對于PCPDIPM 算法，其主要計算量是系數矩陣的形成和修正方程的求解，約占全部計算量的80%～90%。由于新模型的海森矩陣是常量，這極大地減少了形成系數矩陣所需要的時間。對于第2個問題，本文利用列近似最小度COLAMD（column approximateminimumdegree）算法和近似最小度AMD（approximate minimum degree）算法對內點法修正方程的系數矩陣進行節點優化編號，如表2 所示。不管采用哪種排序方法，LU 分解后矩陣的稀疏度都比分解前的要低。對于新模型，除了IEEE14 和IEEE30 節點系統外，COLAMD 算法比AMD 算法有更高的稀疏度；對于常規模型，除了IEEE118 和IEEE300 節點系統外，AMD 算法比COLAMD 算法有更高的稀疏度；由此，COLAMD 算法更適合高階修正方程的系統，更有效地減少了其LU 分解所產生的注入元，從而減少了求解修正方程所需要的時間。

表2 LU 分解前后的稀疏度Tab.2 Degree of sparsity before and after LU %

新模型與常規模型在1 次迭代時形成系數矩陣所需要的時間如表3 所示。可以看出，新模型在1 次迭代時形成系數矩陣所需要的時間比常規模型少，這是因為：由于所提模型是二次模型，其目標函數、等式約束和不等式約束相對應的各個海森矩陣是恒常矩陣，在整個迭代過程中只進行1次計算，導致較少的時間形成修正方程系數矩陣；但對傳統模型而言，由于交流LTC 支路的影響，其模型是高階函數，在每一次迭代過程中都需要求解對應的各個海森矩陣，因此需要更多的時間形成修正方程系數矩陣。

表3 第1 次迭代系數矩陣形成時間Tab.3 Time of forming coefficient matrix in first iteration s

新模型與常規模型在1 次迭代時求解修正方程所需要的時間如表4 所示。兩種模型的系數矩陣經COLAMD 算法優化后（用Ordering 表示）比優化前（用N-Ordering 表示）大大減少了求解修正方程所需要的時間；經COLAMD 算法優化后，新模型求解修正方程所需要的時間比常規模型有所增加，這是由于虛擬節點的引進增加了牛頓方程的階數，但COLAMD 算法對新模型更有效。從表3 和表4 可以看出，求解牛頓方程所增加的計算量小于計算系數矩陣所節省的形成時間，從而導致新模型優化的總時間比常規模型大大減少。

表4 第1 次迭代修正方程求解時間Tab.4 Time of solving correction equation in first iteration

用兩種模型求解最優潮流問題所需要的總時間、迭代次數和運行成本如表5 所示，總時間包括形成海森矩陣、雅可比矩陣、系數矩陣的時間和求解牛頓方程所需要的時間。通過對5 個節點系統仿真，新模型所需要的總時間比常規模型少，系統規模愈大，節省的時間愈多；兩種模型都有相同的迭代次數和優化結果。

為了更好地揭示新模型的收斂特性，表6 列出了IEEE30、IEEE57 和IEEE118 3 個系統在迭代過程中運行成本的變化，仿真結果顯示兩種模型有相同的收斂特性，對一特定系統，迭代過程的前幾次有些不同，但都收斂到相同的結果。

表5 優化總時間、迭代次數和優化結果Tab.5 Time，iterations and optimal results

表6 迭代過程中的燃料費用Tab.6 Fuel cost during the iterative process$/h

3 結語

本文在有載可調變壓器支路中引進虛擬節點，在直角坐標系中建立了包含有載可調變壓器變比的二階最優潮流新模型。該模型的海森矩陣在優化過程中是恒常矩陣，只需要計算1 次，這樣縮短了內點法的計算機消耗總時間。利用列近似最小度法對修正方程系數矩陣進行節點優化排序，進一步減少三角分解過程中注入元的產生。算例結果表明：新模型的迭代特性與傳統模型的基本相同，但優化速度卻有較大的提升。

[1]張勇軍，陳揚華，任震，等（Zhang Yongjun，Chen Yanghua，Ren Zhen，et al）. 計及電壓穩定的最優潮流綜述（Survey on optimal power flow considering voltage stability）[J]. 電力系統及其自動化學報（Proceedings of the CSU-EPSA），2008，20（4）：17-22.

[2]覃智君（Qin Zhijun）.最優潮流的原對偶內點法矢量化實現（Vectorization primal-dual interior point implementation of optimal power flow）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2009，21（5）：68-74.

[3]覃振成，樂秀璠，藍瀾，等（Qin Zhencheng，Le Xiufan，Lan Lan，et al）.基于改進非線性預報-校正內點法的最優潮流（Improved nonlinear predictor-corrector interior point method for optimal power flow）[J].電力系統自動化（Automation of Electric Power Systems），2005，29（9）：25-30.

[4]余娟，顏偉，徐國禹，等（Yu Juan，Yan Wei，Xu Guoyu，et al）.基于預測-校正原對偶內點法的無功優化新模型（A new model of reactive optimization based on predictor corrector primal dual interior point method）[J].中國電機工程學報（Proceedings of the CSEE），2005，25（11）：146-151.

[5]Wei H，Sasaki H，Yokoyama R. An application of interior point quadratic programming algorithm to power system optimization problems[J]. IEEE Trans on Power Systems，1996，11（1）：260-266.

[6]劉沛津，谷立臣，韓行（Liu Peijin，Gu Lichen，Han Xing）.基于內點法與改進遺傳法的無功規劃優化混合算法（Reactive power planning based on IPM and improved GA hybrid method）[J].電力系統保護與控制（Power System Protection and Control），2008，36（17）：56-59.

[7]熊寧，張魏，黃金海，等（Xiong Ning，Zhang Wei，Huang Jinhai，et al）.基于約束松弛變量策略的中心校正內點法（Centrality correction interior point method based on constrained slack variables strategy）[J].電力系統保護與控制（Power System Protection and Control），2012，40（14）：20-25.

[8]Torres G L，Quintana V H. An interior-point method for nonlinear optimal power flow using voltage rectangular coordinates[J].IEEE Trans on Power Systems，1998，13（4）：1211-1218.

[9]Liu Mingbo，Tso S K，Ying Cheng. An extended nonlinear primal-dual interior-point algorithm for reactive-power optimization of large-scale power systems with discrete control variables[J]. IEEE Trans on Power Systems，2002，17（4）：982-991.

[10]王曉東，李乃湖，丁恰（Wang Xiaodong，Li Naihu，Ding Qia）.基于稀疏技術的原對偶內點法電壓無功功率優化（A primal-dual interior point algorithm for optimal voltage/reactive power control with sparsity structure）[J].電網技術（Power System Technology），1999，23（3）：23-26，30.

[11]姚煜，蔡燕春（Yao Yu，Cai Yanchun）.離散粒子群與內點法結合的電力系統無功優化（A hybrid strategy based on DPSO and IPM for optimal reactive power flow）[J]. 電力系統保護與控制（Power System Protection and Control），2010，38（3）：48-52.