基于聚類分析的短期負荷智能預測方法研究＊

陳宏義，李存斌，施立剛?

（1.華北電力大學 經濟與管理學院，北京 102206；2.中國能源建設集團有限公司，北京 100029）

基于聚類分析的短期負荷智能預測方法研究＊

陳宏義1，2，李存斌1，施立剛1?

（1.華北電力大學 經濟與管理學院，北京 102206；2.中國能源建設集團有限公司，北京 100029）

短期電力負荷預測作為電網企業的基本工作，其精度的提高對于電網企業運營管理和調度管理具有較大的意義，然而由于電力負荷受到諸多非線性因素的影響，因此得到高精度的電力負荷預測結果是比較困難的.本文首先利用數據挖掘中的k-means聚類技術對訓練集的氣象數據進行聚類分析，分析提取相似日，在提取相似日的相關歷史數據后，建立支持向量機模型進行短期電力負荷預測.經算例結果證明，由該方法得出的預測結果平均相對誤差為0.88%，和同結構支持向量機預測的平均相對誤差（1.66%）以及ARMA預測的平均相對誤差（3.81%）相比，預測精度得到明顯的提高，證明了該方法的有效性.

數據挖掘；負荷預測；聚類；支持向量機；k-means

隨著電力工業市場化的進展，短期電力負荷預測精度的提高對電網企業的電力調度安排，電網調度自動控制，電網企業的營銷行為具有十分重要的意義［1］.20世紀80年代，國外學者Bunn和Farmer在研究負荷預測精度對電網企業的經濟效益影響時就已經指出，負荷誤差每增加1%將會增加10 000 000英鎊的電力經營成本［2］，因此，負荷預測精度的提高對電網企業而言將會產生較大的社會經濟效益.

很多研究負荷預測的學者已經對電力負荷預測的建模問題開展深入研究，其方法包括回歸擬合預測模型、灰色預測方法、時間序列分析以及幾種方法組合在一起的組合預測方法等.近二十年來，隨著人工智能領域的發展，越來越多的研究人員將神經網絡為代表的人工智能預測方法應用到負荷預測中，取得了一定的成果.其中人工神經網絡由于具有無需先驗經驗便可以按照任意精度進行非線性擬合的優點，受到了眾多學者的青睞，成為近些年來主要的研究方法之一.國內外學者對應用神經網絡進行電力負荷預測的文獻進行了綜述，并指出，和非智能的預測方法相比，神經網絡得到的負荷預測結果精度更高［3－6］.但是也有學者指出利用神經網絡進行預測的缺點是可能收斂于局部最優解，并且在訓練時需要大量的樣本［7］.

支持向量機預測方法的出現極大地改善了神經網絡的上述缺陷，具有要求確定的參數少、在理論上有全局最優唯一解的特點，在小樣本的條件下被認為是可以替代神經網絡的智能預測方法［8］.很多學者針對支持向量機在不同領域內的運用展開研究，均取得了不俗的效果，證明了支持向量機的實用性［9－11］.但是由于短期的負荷預測受到大量復雜影響因素的多重非線性干擾，如氣象、電力的實時需求、經濟影響、電力系統的影響、電力市場各參與方、政治活動等.因此，無論模型如何先進，如果不盡可能地考慮這些因素的影響，很難進一步提高負荷預測的精度.

近幾年，很多學者意識到利用數據挖掘技術首先對數據進行處理，再利用模式識別技術提取出相應的負荷預測影響相關的知識，能夠進一步提高預測的精度.在提取出的相關知識里，尤其是氣象相關的知識，如分類［12］、尋找相似日特征［13］等對提高負荷預測的精度作用最大.這表明將數據挖掘技術引入到電力負荷預測中不但是可行的，而且可以提高預測的精度.受此思路啟發，本文首先利用待預測日的氣象因素，采用數據挖掘中的k-means聚類算法進行聚類，得到相似日的結果，然后提取相似日的相關歷史負荷數據，并利用支持向量機模型對負荷進行預測.由于該預測方法在建模前，首先通過聚類方法找出和待預測日相似的負荷數據樣本進行短期負荷預測，因此和傳統預測方法利用近期樣本進行預測相比，能夠有效地進一步提高負荷預測的精度.

1 利用k-means聚類方法選取相似日數據

聚類分析是對樣本或指標按照各自的特性進行

其中E是所有樣本的平方誤差的總和；p是聚類空間中的樣本點；mi是簇Ci的平均值.

由于短期電力負荷預測受到較多因素的影響，因此能否針對待預測日，利用和待預測日相近日的數據進行預測是進一步提高短期電力負荷預測精度的一個關鍵步驟.這是因為利用數據挖掘在預測前先選取相似日可以將具有高度相似特征的類似負荷點尋找出來，尤其在利用智能算法對負荷進行預測時，可以避免由于具有不同特征的預測點對智能預測方法訓練時產生的收斂慢的問題.利用k-means聚類方法提取相似日電力負荷數據，結合智能預測模型進行預測的流程如下：

1）針對待預測日／時點，收集相關預測影響因素的數據，如天氣，日期類型等，組成一條數據記錄；

2）對上述數據記錄，針對歷史負荷數據中的數據，設定聚類個數k，利用k-means算法進行聚類尋找；

3）根據聚類結果，記錄日期標識，按照預測的“近大遠小”原則，選擇距離待預測日最近日期的相分類的一種多元統計分析方法，一般基于距離的標準對樣本數據分成不同的類或者簇.和分類相比，聚類不需要先驗知識，即，可以在無監督、無指導的條件下進行機器學習.聚類目前應用于很多領域中，包括數學、計算機科學、統計學、生物學和經濟學等.聚類算法主要以統計方法、機器學習、智能計算等方法為基礎，其中較著名的聚類方法是k-means劃分算法，也是最具有代表性的聚類方法之一.該算法只需要一個參數，即聚類個數k，然后將樣本n分為k個簇，分類原則是具有較高相似度的盡量劃分為一個簇，而不同簇之間的相似度則盡可能的小.k-means算法過程如下［14］：

1）從n個樣本中任選k個對象作為簇中心；

2）計算中心外樣本和中心之間的相似度（一般采用距離函數）；

3）按照相似度進行分配，具有較高相似度的樣本聚類為一簇；

4）計算聚類后所得簇的新的簇中心，并不斷重復，直到標準測度函數開始收斂為止.

k-means聚類的標準測度函數一般采用如式（1）所示的均方差予以計算：關歷史負荷數據，確定出待預測日的輸入因素，建立智能預測模型進行預測.

2 支持向量機預測模型

本文的智能預測模型選取的是支持向量機（support vector machine，SVM），該模型是 Vapnik于20世紀90年代中期提出的一種新的智能學習方法，起先用于非線性的模式識別問題，隨著應用領域的不斷擴展和對支持向量機研究的深入，支持向量機逐漸應用于非線性的擬合中，表現出了良好的性能，并且由于支持向量機利用結構風險最小化代替了神經網絡的經驗風險最小化對網絡結構進行訓練，因此具有較好的泛化能力，在理論上能夠搜索到全局最優解，能夠克服神經網絡易陷入局部最小值的缺點.由于支持向量機在小樣本的條件下學習速度快，因此可以認為支持向量機方法是可以在小樣本條件下取代神經網絡方法的較好的選擇.

支持向量機進行非線性擬合預測方法的原理如下［1］.

假設有訓練樣本集 G ＝ ｛（xi，di）｝，i＝1，…，N，xi∈Rn，di∈R1.支持向量機回歸的基本原理是通過映射將數據映射到一個高維特征空間中，并在該空間中尋找一個輸入空間到輸出空間的非線性映射 ψ（x），其回歸函數如下：

其函數逼近問題等價于如下函數最小：

通過引入兩個松弛變量ζ，ζ＊，上述函數可以變成如下形式：

利用拉格朗日型和Karush-Kuhn-Tucker條件，解其對偶問題，可以得到支持向量機回歸函數：

3 實證分析

本文以我國南方電網某地市級電力局的日整點負荷數據為例進行實證分析.利用聚類分析的因素數據有日期類型數據、氣象數據（包括氣壓相關數據、氣溫相關數據、濕度相關數據、降水量、人體舒適程度等）共12項屬性相關數據，共組織形成54條記錄形式，將最后1條數據作為測試記錄使用.其具體數值如表1所示.

接下來對這些記錄進行預處理，對于標識型的數據，利用數值予以替代.以星期為例，分別用0，1，…，6代替星期日，星期一，…，星期六，對于原本是數據類型的屬性值，利用等距離方法將其離散化，從而得到初始分析記錄集.

對于支持向量機模型的訓練，按照相關文獻，將輸入層節點選取L（t－24i），L（t－j），其中i＝1，2，3；j＝1，2，即，使用待預測時點的前三個時點和同一聚類中的日期待預測時間最近兩天的同一時點的數據作為輸入變量.此外，為方便對比分析，選取同結構的支持向量機，即，使用待預測時點的前三個時點和前兩天的同一時點數據作為輸入變量，同時，利用自回歸滑動平均模型ARMA（1，1）對上述數據分別進行預測.實驗計算環境選擇matlab2011a，libsvm2.8.8軟件包，誤差對比分析采用平均相對誤差eMAPE，計算結果如表2所示.

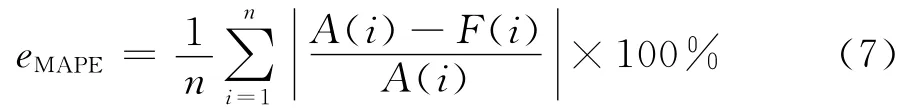
從圖1和表2中可以明顯發現，本文提出的方法具有較高的精度值，并且在大多數預測點上均表現良好，平均誤差值達到了0.88%，而同結構未進行聚類尋找相似數據的支持向量機預測的平均誤差為1.66%，根據 ARMA（1，1）得到的預測平均誤差為3.81%.從誤差對比中可以直觀地看出，本文的方法具有更高的擬合精度.

表1 處理后的待聚類數據集Tab.1 Cluster’s data set to be processed

圖1 3種方法預測結果曲線圖Fig.1 The forecasting result with three models

表2 不同方法得出的預測結果Tab.2 Forecasting result from different methods

4 結 論

1）通過實例分析證明，支持向量機的預測結果高于傳統的時間序列分析方法，說明智能預測方法較傳統的預測方法結果更優.

2）本文將數據挖掘的k-means和支持向量機預測方法相結合，利用聚類技術提取歷史數據集中的相似數據后，再利用支持向量機進行預測，能夠更進一步提高預測精度.

［1］ 王建軍.智能挖掘電力負荷預測研究及應用［M］.北京：中國水利水電出版社，2013.

WANG Jian-jun.Collaborative intelligence and knowledge mining technology for load forecasting method and application［M］.Beijing：China Water ＆ Power Press，2013.（In Chinese）

［2］ BUNN D W，FARMER E D.Comparative models for electrical load forecast［M］.New York：John Wiley，1985.

［3］ 胡暉，楊華，胡斌.人工神經網絡在電力系統短期負荷預測中的應用［J］.湖南大學學報：自然科學版，2004，31（5）：51－53.

HU Hui，YANG Hua，HU Bin.Application of artificial ANN to short-term load forecasting in power system［J］.Journal of Hunan University：Natural Sciences，2004，31（5）：51－53.（In Chinese）

［4］ 曾鳴，劉寶華，徐志勇，等.基于混沌模糊神經網絡方法的短期負荷預測［J］.湖南大學學報：自然科學版，2008，35（1）：58－61.

ZENG Ming，LIU Bao-hua，XU Zhi-yong，et al.Short-term load forecasting based on artificial neural network and fuzzy theory［J］.Journal of Hunan University：Natural Sciences，2008，35（1）：58－61.（In Chinese）

［5］ 彭顯剛，胡松峰，呂大勇.基于RBF神經網絡的短期負荷預測方法綜述［J］.電力系統保護與控制，2011，39（17）：144－148.｀

PENG Xian-gang，HU Song-feng，LV Da-yong.Methods of short-term load forecasting based on RBF neural network［J］.Power System Protection and Control，2011，39（17）：144－148.（In Chinese）

［6］ HENRIQUE Steinherz Hippert，CARLOS Eduardo Pedreira，REINALDO Castro Souza.Neural networks for short-term load forecasting：a review and evaluation［J］.IEEE Transactions on Power Systems，2001，16（1）：44－55.

［7］ ENGIN Avci.Selecting of the optimal feature subset and kernel parameters in digital modulation classification by using hybrid genetic algorithm-support vector machines：HGASVM［J］.Expert Systems with Applications，2009，36（2）：1391－1402.

［8］ 李元誠，方廷健，于爾鏗.短期負荷預測的支持向量機方法研究［J］.中國電機工程學報，2003，23（6）：55－59.

LI Yuan-cheng，FANG Ting－jian，YU Er-keng.Study of support vector machine for short-time load forecasting［J］.Proceedings of the CSEE，2003，23（6）：55－59.（In Chinese）

［9］ 袁小芳，王耀南，孫煒，等.一種用于RBF神經網絡的支持向量機與BP的混合學習算法［J］.湖南大學學報：自然科學版，2005，32（3）：88－92.

YUAN Xiao-fang，WANG Yao-nan，SUN Wei，et al.A hybrid learning algorithm for RBF neural networks based on support vector machines and BP algorithms［J］.Journal of Hunan University：Natural Sciences，2005，32（3）：88－92.（In Chinese）

［10］耿艷，韓學山，韓力.基于最小二乘支持向量機的短期負荷預測［J］.電網技術，2008，32（18）：72－76.

GENG Yan，HAN Xue-shan，HAN Li.Short-term load forecasting based on least squares support vector machines［J］.Power System Technology，2008，32（18）：72－76.（In Chinese）

［11］張瑩，王耀南，文益民.啤酒瓶檢測中多分類支持向量機算法的選擇［J］.湖南大學學報：自然科學版，2009，36（5）：37－41.

ZHANG Ying，WANG Yao-nan ，WEN Yi-min.Choice of multi-class support vectormachines on beer bottle detection［J］.Journal of Hunan University：Natural Sciences，2009，36（5）：37－41.（In Chinese）

［12］牛東曉，谷志紅，邢棉，等.基于數據挖掘的SVM短期負荷預測方法研究［J］.中國電機工程學報，2006，26（18）：6－12.

NIU Dong-xiao，GU Zhi-hong，XING Mian，et al.Study on forecasting approach to short-term load of SVM based on data mining［J］.Proceedings of the CSEE，2006，26（18）：6－12.（In Chinese）.

［13］栗然，劉宇，黎靜華，等.基于改進決策樹算法的日特征負荷預測研究［J］.中國電機工程學報，2005，25（23）：36－41.

LI Ran，LIU Yu，LI Jing-hua，et al.Study on the daily characteristic load forecasting based on the optimizied algorithm of decision tree［J］.Proceedings of the CSEE，2005，25（23）：36－41.（In Chinese）

［14］KRISTA Rizman Zalik.An efficient k-means clustering algorithm［J］.Pattern Recognition Letters，2008，29（9）：1385－1390.

A New Forecasting Approach for Short-term Load Intelligence Based on Cluster Method

CHEN Hong－yi1，2，LI Cun-bin1，SHI Li-gang1?
（1.School of Economics and Management，North China Electric Power Univ，Beijing 102206，China；2.China Energy Engineering Group Co Ltd，Beijing 100029，China）

Load forecasting is one of the basic issues of the electric power industry.However，because load has a certain social attributes，the improvement of the accuracy of load forecasting result is a difficult issue.This paper first used k-means cluster method to find similar data from historical date and weather data，and then used support vector machine（SVM）for forecasting.Seen from the result，the proposed method＇s MAPE is 0.88%，but BP-ANN and ARMA are 1.66%and 3.81%respectively.It is proved that this method has a high accuracy.

data mining；load forecasting；clustering；support vector machine（SVM）；k-means

TM715

A

1674-2974（2014）05-0094-05

2013-12-22

國家自然科學基金資助項目（71271084）；國家電網公司2014年總部科技項目6-5

陳宏義（1966－），男，湖南漢壽人，中國能源建設集團有限公司高級政工師，華北電力大學博士研究生

?通訊聯系人，E-mail：shlg87＠163.com