心形線雙曲拱壩三維建模

趙海峰， 杜廷娜， 葉榮波， 趙海波

（1. 重慶交通大學，重慶 400074；2. 同興源工程勘察設計有限公司，四川 成都 610000；3. 安徽省建設工程勘察設計院北京分院，北京 100039）

心形線雙曲拱壩三維建模

趙海峰1， 杜廷娜1， 葉榮波2， 趙海波3

（1. 重慶交通大學，重慶 400074；2. 同興源工程勘察設計有限公司，四川 成都 610000；3. 安徽省建設工程勘察設計院北京分院，北京 100039）

心形線作為幾何數學上最美最浪漫的一條曲線，第一次在拱壩設計中研究應用。在研究心形線幾何特性時，發現有一段非常扁平的曲線，作為拱壩中軸線非常適合，可以使得拱壩的合力方向向山里偏轉，有利于壩肩的穩定。因此，研究心形線作為拱壩的一種新線形，理論上具有可行性，并在實際工程中有一定的應用參考價值。該文在研究心形線雙曲拱壩各種參數的基礎上，建立心形線雙曲拱壩的數學方程，實現圖形的三維建模，為拱壩下一步進行有限元分析提供精確的三維模型，也為今后拱壩壩型的設計提供更多的選擇和有意義的參考。

計算機應用；心形線；中軸線；雙曲拱壩；三維建模

心形線最早是由法國著名的哲學家、科學家和數學家勒內·笛卡爾(Rene Descartes)提出的，心形線的形成是由動圓上的一個固定點，繞著與其相切且半徑相同的另外一個固定的基圓圓周滾動時所形成的軌跡，因其形狀像心形而得名。

心形線作為數學上浪漫而優美的曲線，其本身的魅力不僅受到了數學家們的青睞，同時在生活中也得到了廣泛的應用。人們在研究笛卡爾提出的心形線時，根據其幾何意義和物理意義研發出先進的技術產品，使其數理意義得到升華；同理，在工程上的應用，通過與實際工程結合，發現心形線具有創新與發展的廣闊空間。在心形線參數變化過程中，可以得到一段非常扁平的曲線，這與拱壩設計中拱圈中軸線的線型選擇相當契合。當拱壩設計者審慎地對壩基勘探和處理后，希望壩體體形也趨于扁平化，使拱端的合力方向向山里偏轉，以利于壩肩的穩定。這意味著，心形線雙曲拱壩很可能在某些方面會優于其他圓弧或非圓弧雙曲拱壩。因此，本文研究了心形線雙曲變厚拱壩的幾何建模，并利用C++語言編程，進而在CAD平臺上得到心形線雙曲拱壩的仿真形體，為拱壩下一步進行有限元分析提供精確的三維體型[1]。

1 心形線

1.1 心形線的方程

心形線極坐標方程：

式中，r為極徑，a為基圓的直徑，θ為極角。兩個方程分別對應不同方向上的圖形，圖1所示為垂直方向上其中一個方程的圖形。

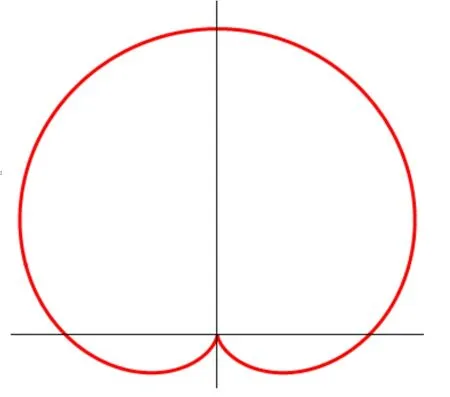
圖1 r=a×(1 +sinθ)的心形線圖形

根據上述極坐標方程可以得到心形線的參數方程：

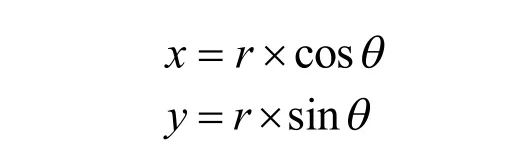
再根據心形線的參數方程，我們得到其直角坐標方程：

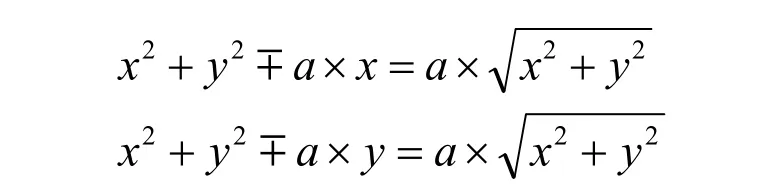
1.2 心形線的性質

心形線可以是一垂足曲線，同時也是圓的包絡線，并且對于任意斜率，心形線都擁有三條互相平行的切線。心形線包圍的面積為心形線的周長為 8a。

1.3 心形線的應用領域

心形線的出現首先來源于大自然的鬼斧神工以及生物的物競天擇，比如心形的島嶼、湖泊、濕地、森林、珊瑚礁等，這就引起了人們用數學語言，幾何方式去詮釋這種自然現象的興趣，并促進了心形線在各個工程領域的應用，并開發成各種工業產品，例如心形線電話筒，手機，發動機等。

2 心形線拱壩數學模型

為方便研究和量化說明，現以國內某工程實例為依托，建立數學模型。可以將拱壩看成由若干水平拱圈按照一定的規律連續變化而形成[2]，因而，對拱壩形體的數學模型研究可以轉化為對拱圈數學模型的研究[3]。

2.1 心形線拱圈中軸線方程的建立

心形線拱圈中軸線方程的建立主要受到工程所處的地形地質參數，以及拱壩中心角選取的影響[4]。由于心形線在拱圈線形中的應用在國內外尚未出現，但依據拱壩設計規范，水平拱圈的最大中心角應根據應力、穩定性、工程量等因素，選為75°～110°。因此，結合已建工程的經驗，我們設定了最大的中心角，以及壩頂和其他拱圈的中心角；根據已得到的中心角φ，由心形線的極角θ與拱圈中心角的關系，可以計算得到參數方程的極角數值；再根據各層拱圈的水平間距L，結合心形線的參數方程，最終得到每一層拱圈中軸線的坐標值。圖2所示為心形線作為拱壩中軸線的坐標計算圖形。

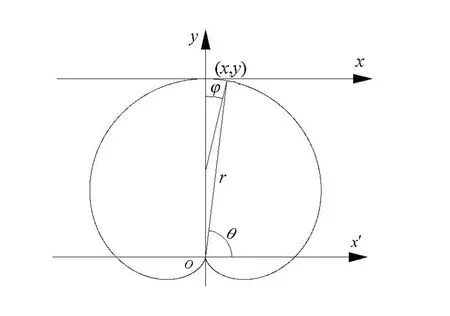
圖2 心形線的坐標圖形

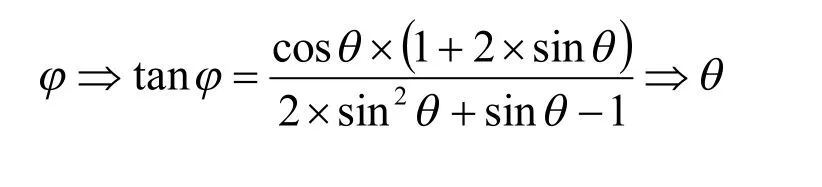
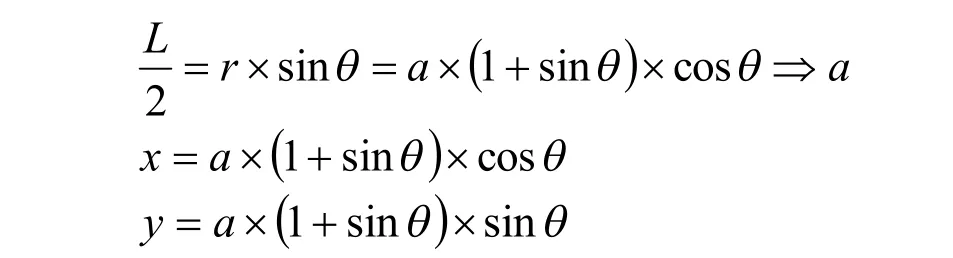
拱圈中軸線的頂點一般都是位于坐標原點的，因此由上述方程得到的坐標還需要將縱坐標進一步變換，即：

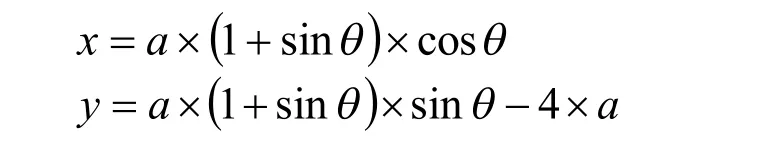
2.2 心形線拱圈上下游拱弧方程的推導

拱圈上下游的坐標主要是根據密切圓包絡線法得到，以中軸線上的點為圓心，再根據相應中心角，以及相對應的厚度為直徑，當這些密切圓足夠多足夠緊密時，可以擬合出上下游拱圈[5]，如圖3所示。

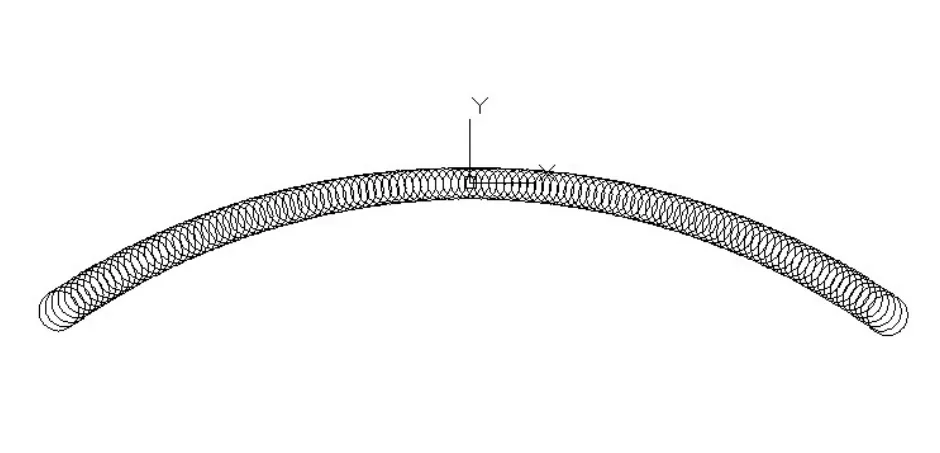
圖3 心形線包絡圓擬合拱圈的圖形

再由拱圈通用公式確定拱圈上下游面的坐標[4]，其中左半拱為：

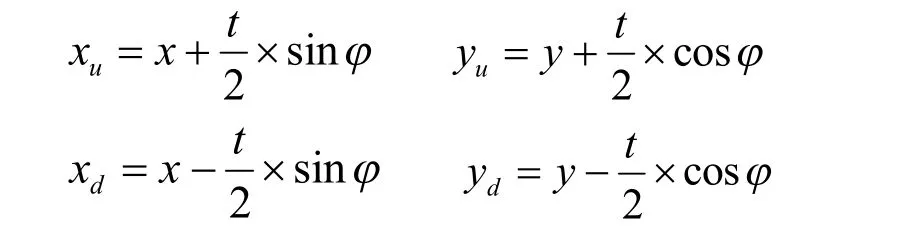
右半拱：

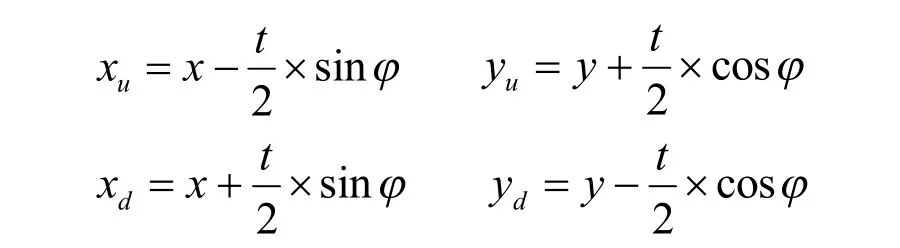
式中， xu， yu為拱圈上游面的坐標； xd， yd為拱圈下游面的坐標；t為拱圈的厚度。

經驗表明，拱座的彎矩一般大于拱冠的彎矩，因此，拱座的應力通常大于拱冠，為了節省混凝土，壩體厚度應由拱冠向拱座逐漸增加，這種厚度的變化是漸變的，厚度 t隨角度φ變化的方程為：

式中， tc， tAR， tAL分別為拱冠、右拱座、左拱座的厚度；γ 為指數。

根據以上拱圈每一角度對應的厚度，以及中軸線的坐標，即可得出上下游的坐標，進而得到上下游曲線，如圖4所示。

圖4 拱圈上下游坐標圖形

3 拱壩三維實體模型的編程與實現

3.1 C++編程的主要代碼

通過以上方程的推導，如果用一般方法計算是相當繁瑣的[6]。尤其是在拱圈要求擬合的非常平滑過程中，更是要對中心角進行0.1°的劃分，這樣計算的復雜性與重復性將是手動無法完成的，因此只能用程序化來實現最終圖形。現利用C++語言編制心形線雙曲變厚拱壩程序，其主要程序代碼如下：

3.2 CAD生成三維實體模型

根據以上C++程序，首先生成后綴為scr的文件，然后將文件導入AutoCAD平臺中，這樣就可以自動生成拱壩線框模型，如圖5所示。

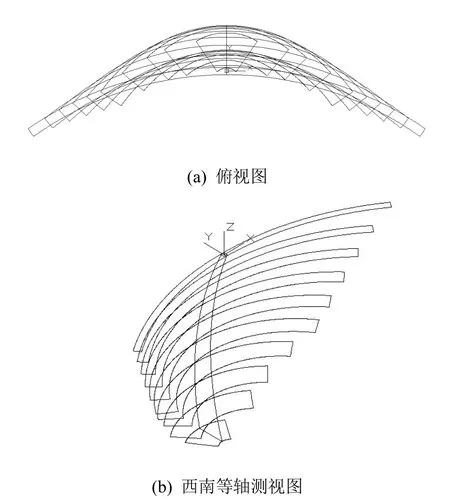
圖5 心形線雙曲拱壩的線框模型

但這僅僅是拱圈的線框模型，為了更好的模擬拱壩體型，以及在實際工程中進行應力與應變的分析模擬測試，需要對這些線框模型在 CAD中進行放樣來生成三維實體模型。但由于每一層拱圈都是以0.1°來劃分取點的，這就導致拱圈的點相對較多，圖形的數據量會很大，軟件處理起來會相對較慢，由于計算機本身的限制，本次計算機模擬只能一層一層的進行放樣；又因為每一層拱圈所對應的中心角是不同的，這就導致了上一層拱圈與下一層拱圈上的點數不一致的情況，這就要求在放樣的過程中需要注意調節與控制，避免出現圖形的扭曲。拾取上一層拱圈與下一層拱圈的點盡量相同，可以取得比較理想的三維形體。本次放樣主要拾取的是左半拱圈的下游起點，這樣就可能減少不必要的扭曲，最終得到三維實體模型，如圖6所示。再通過不同視角的渲染輸出，就可得到拱壩的渲染圖形，如圖7所示。

圖6 心形線雙曲拱壩的實體模型

圖7 心形線雙曲拱壩三維渲染模型

4 結 論

心形線在拱壩線形中的理論研究與實際應用之前都沒有出現過，本文尚屬第一次，因此，為了更合理的、更充分的說明其在拱壩線形中應用的合理性，嘗試了在相同的地形參數，中心角參數的情況下，心形線作為拱圈中軸線與拋物線作為拱圈中軸線的對比，如圖8所示。

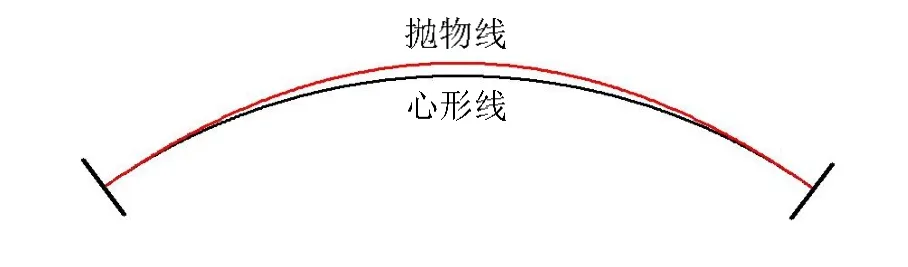
圖8 心形線與拋物線作為中軸線的對比

從圖8中我們可以清楚地看到，心形線的線形明顯要比拋物線的線形要扁平，這必然會使得拱壩兩邊壩肩的應力方向更加向山里的巖基偏轉，從而減少壩肩向下游滑動的因素；同時，由于心形線的弧長也小于拋物線的弧長，這也將有利于減少澆筑拱壩混凝土的體積。

在結合已建工程的基礎上，嘗試了心形線雙曲變厚拱壩的創新設計與研究，并且通過數學幾何建模，C++語言編程，AutoCAD三維建模，最終得到了心形線雙曲變厚拱壩三維實體模型。該模型可以作為有限元分析軟件的原始模型，為下一步實現應力分析與體型優化奠定基礎[7]。心形線在拱壩上的應用還沒出現，包括其在工程上的應用也相對不多，但作為一種參數化的優美曲線，其本身具備數學建模以及聯系工程實際的特性，因此，心形線雙曲變厚拱壩的提出及體型優化將為新的拱壩研究與發展提供理論基礎和科學依據。

[1] 潘家錚. 拱壩[M]. 北京: 水利電力出版社, 1982: 21-25.

[2] 朱伯芳. 中國拱壩的建設的成就[J]. 水利發電, 1999, 45(10): 38-40.

[3] 朱伯芳, 高季章, 陳祖煜, 厲易生. 拱壩設計與研究[M].北京: 中國水利水電出版社, 2002: 52-56.

[4] 周 偉, 葉 林, 李蒲建, 宋衛峰. 對數螺旋線與對數螺旋型拱壩研究[J]. 電網與水力發電進展, 2008, (3): 66-69.

[5] 歐陽建國. 拱壩CADC的理論與實踐[M]. 武漢: 武漢大學出版社, 2003: 41-45.

[6] 林繼鏞. 水工建筑物[M]. 北京: 中國水利水電出版社, 2009: 143-146.

[7] 陳曉年, 常曉林. 拱壩體形優化研究進展[J]. 湖北水利發電, 2008, 76(3): 31-35.

3D Modeling of Cardioid Dome Dam

Zhao Haifeng1, Du Tingna1, Ye Rongbo2, Zhao Haibo3
(1. Chongqing Jiaotong University, Chongqing 400074, China; 2. Tong Xingxuan Engineering Survey and Design Limited Company, Chengdu Sichuan 610000, China; 3. Construction Survey and Design Institute of Anhui Province, Beijing Branch, Beijing 100039, China)

As the most beautiful and the most romantic curve, the cardioid is designed and applied in arch dam for the first time. In researching the geometric characteristics of cardioid, we find a length of very flat curve in it, which is suitable as the axle wire of arch dam, for it can make the resultant force direction of arch dam deflect to the mountain. Therefore, it has a certain applicable value to research cardioid as a new line type of arch dam. Based on researching various parameters of cardioid dome dam, this article establishes mathematical equations of cardioid dome dam, and adopts 3D modeling. It will provide an accurate model for finite element analysis in next step. And it will also provide more selections and meaningful reference for arch dam designing.

computer application; cardioid; axle wire; dome dam; 3D modeling

TP 339

A

2095-302X (2014)02-0195-05

2013-03-10；定稿日期：2013-03-26

重慶交通大學國家內河航道整治工程技術研究中心開放基金資助項目（SLK2010A01）

趙海峰（1987-），男，河南安陽人，碩士研究生。主要研究方向為水利工程。E-mail：robbert378@sohu.com