五階與六階三角樣條曲線

嚴蘭蘭， 韓旭里， 黃 濤

（1. 東華理工大學理學院，江西 南昌 330013；2. 中南大學數學與統計學院，湖南 長沙 410083）

五階與六階三角樣條曲線

嚴蘭蘭1,2， 韓旭里2， 黃 濤1

（1. 東華理工大學理學院，江西 南昌 330013；2. 中南大學數學與統計學院，湖南 長沙 410083）

利用三角函數構造了兩個含參數的函數組，它們分別由6個、7個函數組成，分析了這兩個函數組的性質。由這兩組函數定義了兩種新的樣條曲線，它們分別具有與五次、六次B樣條曲線相同的結構。新曲線在繼承B樣條曲線基本性質的同時，又具備了一些新的優點。例如，在等距節點下，新曲線在節點處均可以達到C5連續，而且在不改變控制頂點的情況下，新曲線的形狀均可以通過改變形狀參數的值進行調整。另外，給出了使新曲線插值于控制多邊形首末端點的方法，以及構造閉曲線的方法等，文中的圖例說明了新方法的正確性和可行性。

曲線設計；三角函數；樣條曲線；形狀參數；連續性

B樣條方法具有表示與設計自由型曲線曲面的強大功能，是最廣泛流行的形狀數學描述的主流方法之一。雖然如此，B樣條方法依然可以繼續改進。為了使B樣條曲線的形狀可以在不改變控制頂點的情況下自由調整，文獻[1-3]通過在基函數中加入參數來實現這一目標。為了使B樣條曲線可以精確表示橢圓、擺線、螺旋線等，文獻[4-5]通過在三角函數空間上構造基函數來實現這一目標。為了使B樣條曲線可以精確表示雙曲線、懸鏈線等，文獻[6-8]通過在雙曲函數空間上構造基函數來實現這一目標。為了使B樣條曲線可以達到更高階的連續性，文獻[9-15]通過構造特殊的三角基函數來實現這一目標。此外，文獻[9-15]中定義的曲線均具有形狀可調性，另文獻[11-15]中定義的曲線均可以表示橢圓。

為了進一步豐富三角樣條曲線造型方法，繼文獻[14]定義了結構與性質類似于三次B樣條曲線的三角樣條曲線，文獻[15]定義了結構與性質類似于四次B樣條曲線的三角樣條曲線之后，這里分別定義了結構和性質類似于五次、六次B樣條曲線的三角樣條曲線。新曲線的優點在于不僅具有形狀可調性，而且還可以達到較高階的連續性。

雖然與五次、六次B樣條曲線相比，因為采用三角函數作為基函數，五階、六階三角樣條曲線的計算量有所增加。但五次均勻B樣條曲線在節點處只能達到C4連續，雖然六次均勻B樣條曲線在節點處可以達到C5連續，但當控制頂點和節點向量給定后，五次、六次B樣條曲線的形狀便都被唯一確定了，要想修改它們的形狀，必須調整控制頂點或節點向量，重新計算曲線方程。而這里即將給出的五階、六階均勻三角樣條曲線除了在節點處可以達到C5連續之外，還可以在不改變控制頂點和節點向量的情況下，通過改變形狀參數的取值方便有效地調整曲線的形狀，因此這里為采用三角函數所付出的的增加計算量的代價是有理論和現實意義的。

1 函數組的構造與性質

為五階三角樣條函數；稱函數

為六階三角樣條函數。

將三角樣條函數中的各函數沿參數軸首尾相連，則構成一條完整的三角樣條。圖1和圖2分別為取不同參數時得到的五階、六階三角樣條。

圖1 五階三角樣條函數

圖2 六階三角樣條函數

五階、六階三角樣條函數具有下列性質：

（1）退化性：當 λ= 1時， b50(t)= b55(t)= 0，五階三角樣條函數成為文獻[11]中取 λ=1時的基函數，文獻[12]中取 m= 3時的調配函數，文獻[14]中取時的 β- B基；當 λ= 1時，b60(t)= b66(t)= 0，六階三角樣條函數退化為文獻[15]中取 α=1時的 α- B基。

（2）非負性： b (t) ≥ 0(n= 5,6;i=0,1,…,n)。

2 曲線的構造與性質

定義2：給定控制頂點 P ∈ Rd(d = 2,3;i =0,1,

i… ,n)和節點向量 U=(u-4,u-3,…,un+2)，其中u-4＜ u-3＜ … ＜un+2。對于 i= 1,2,… ,n -4，定義

為五階三角樣條曲線段，所有曲線段構成樣條曲線

為六階三角樣條曲線段，所有曲線段構成樣條曲線

五階、六階三角樣條曲線具有下列性質：

（1）凸包性：由五階、六階三角樣條函數的非負性和規范性可知，由式(7)確定的曲線段位 于 由 控 制 頂 點形成的凸包 Hi內，由式(8)確定的整條曲線 p(u)位于所有凸包 Hi的并集內；由式(9)確定的曲線段位于由控制頂點形成的凸包 Ti內，由式(10)確定的整條曲線 q(v)位于所有凸包 Ti的并集內。

（2）幾何不變性：由五階、六階三角樣條函數的規范性可知，五階、六階三角樣條曲線的形狀均與坐標系的選取無關。

（3）對稱性：由五階、六階三角樣條函數的對稱性可知，將五階、六階三角樣條曲線的控制多邊形順序取反，將定義同一條曲線，僅曲線方向取反。

（4）連續性：由五階、六階三角樣條函數的端點性質式(3)～式(6)，以及五階、六階三角樣條曲線段的定義式易知

結合式(11)～式(13)有

其中， k= 0,1,… ,5，這說明五階、六階三角樣條曲線均 G5連續，均勻五階、六階三角樣條曲線均C5連續。

（5）形狀可調性：由于五階、六階三角樣條函數的表達式中均含有參數λ，故在不改變控制頂點的情況下，五階、六階三角樣條曲線的形狀均可以通過改變參數λ的值進行調整。

圖3和圖4分別為取不同參數時得到的五階、六階三角樣條曲線，圖中虛線為控制多邊形。從圖中可以看出，參數λ的值越大，五階、六階三角樣條曲線越逼近其控制多邊形。

圖3 五階三角樣條曲線

圖4 六階三角樣條曲線

3 曲線設計

開曲線與閉曲線的構造是曲線設計中最基本的內容，人們需要了解開曲線的端點行為和如何構造閉曲線。

由式(3)、式(4)、式(7)、式(8)可知，由控制頂點 P0,P1,… ,Pn定義的五階三角樣條曲線的起點、終點分別為由式(14)、式(15)可知：若記 P0與 P4的中點為， P1與 P3的中點為，則曲線的首點位于以邊（位于邊上，起點為 P，2長度為邊的長度的倍）和（位于邊上，起點為 P2，長度為邊的長度的倍）為鄰邊形成的平行四邊形的對角線（起點為 P2）的終點處。對于終點也有相似的結論。

方法1：先在邊 P0P1上任取一點記作，在邊 Pn-1Pn上任取一點記作，再由公式

方法2：先由公式

圖5給出了在初始控制多邊形相同的情況下，由不同方法得到的插值于控制多邊形首末頂點的五階三角樣條曲線。圖5(a)中的曲線是采用第一種方法得到的，圖5(b)中的曲線是采用第二種方法得到的。

圖5 插值于控制多邊形首末頂點的五階三角樣條曲線

若控制多邊形 P0P1… Pn是封閉的，即P0= Pn，為了使由之定義的五階三角樣條曲線也是封閉的，只需增加 4 個輔助頂點再由控制多邊形定義五階三角樣條曲線即可（見圖6(a)）。倘若不僅要求曲線封閉，而且要求曲線插值于控制多邊形的首末頂點，即插值于點 P0(Pn)， 則 不 需 先 增 加 輔 助 頂 點而只需直接按照上一段所陳述的兩種方法增加輔助頂點即可（見圖6(b)）。

圖6給出了由封閉控制多邊形定義的封閉的五階三角樣條曲線。圖6(a)中的曲線僅僅是封閉的，圖6(b)中的曲線不僅封閉而且插值于控制多邊形的首末頂點。

圖6 封閉的五階三角樣條曲線

由式(5)、式(6)、式(9)、式(10)可知，由控制頂點 P0,P1,… ,Pn定義的六階三角樣條曲線的起點、終點分別為

由式(16)、式(17)可知：若記 Q0與 Q5的中點為Q1與 Q4的中點為Q2與 Q3的中點為則曲線的起點位于以邊（位于邊上，起點為Q23，長度為邊的長度的倍）和（位于邊上，起點為長度為邊的長度的倍）為鄰邊形成的平行四邊形的對角線（起點為Q23）的終點處。對于終點也有相似的結論。

方法1：先在邊 Q0Q1上任取兩點記作使點順序排列，在邊 Qn-1Qn上任取兩點記作使點順序排列，再由公式確定輔助頂點然后由控制多邊形定義曲線即可（見圖7(a)）。

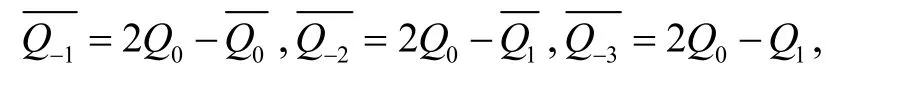
方法2：先在邊 Q0Q1上任取一點記作，在邊上任取一點記作，再由公式

圖7給出了在初始控制多邊形相同的情況下，由不同方法得到的插值于控制多邊形首末頂點的六階三角樣條曲線。

圖7 插值于首末控制頂點的六階三角樣條曲線

若控制多邊形 Q0Q1… Qn是封閉的，即Q0= Qn，為了使由之定義的六階三角樣條曲線也封閉，只需增加 5 個輔助頂點再由控制多邊形定義曲線即可（見圖8(a)）。倘若不僅要求曲線封閉，而且要求曲線插值于控制多邊形的首末頂點，則只需直接按照上一段所陳述的兩種方法增加輔助頂點即可（見圖8(b)）。

圖8給出了由封閉控制多邊形定義的封閉的六階三角樣條曲線。圖8(a)中的曲線僅僅是封閉的，圖8(b)中的曲線不僅封閉而且插值于控制多邊形的首末頂點，其中由內至外的曲線分別取參數

圖9和圖10 分別給出了五階、六階三角樣條曲線的圖形實例。圖9中由大到小的星形曲線分別為由五角星形的控制多邊形（點線線）和參數λ= 0,1所確定的五階三角樣條曲線。圖10中的曲線為由圖中控制多邊形（點線）和參數 λ=1所確定的六階三角樣條曲線。

圖8 封閉的六階三角樣條曲線

圖9 星形圖案

圖10 手掌圖案

4 總 結

[1] Wang Wentao, Wang Guozhao. Uniform B spline with shape parameter [J]. Journal of Computer-Aided Design & Computer Graphics, 2004, 16(6):783-788.

[2] Han Xuli. Piecewise quartic polynomial curves with a local shape parameter [J]. Journal of Computational and Applied Mathematics, 2006, 19(5): 34-45.

[3] 張貴倉, 耿紫星. 三次均勻B樣條曲線的α擴展[J].計算機輔助設計與圖形學學報, 2007, 19(7): 884-887.

[4] 呂勇剛, 汪國昭, 楊勛年. 均勻三角多項式 B樣條曲線[J]. 中國科學(E輯), 2002, 32(2): 281-288.

[5] 蘇本躍, 黃有度. T-B樣條曲線及其應用[J]. 大學數學, 2005, 21(1): 87-90.

[6] 鄔弘毅, 左 華. 多形狀參數的二次非均勻雙曲 B樣條曲線[J]. 計算機輔助設計與圖形學學報, 2007, 19(7): 876-883.

[7] 陸利正, 汪國昭. 二次帶形狀參數雙曲B-樣條曲線[J].高校應用數學學報A輯, 2008, 23(1): 105-111.

[8] 謝 進, 檀結慶, 李聲鋒. 含有權參數的二次代數雙曲B樣條曲線[J]. 高等學校計算數學學報, 2011, 33(4): 337-346.

[9] 嚴蘭蘭, 梁炯豐. 三種形狀可調三角樣條曲線[J].計算機工程與應用, 2010, 46(21): 191-194.

[10] 嚴蘭蘭, 梁炯豐. 兩種帶形狀參數的曲線[J]. 計算機工程與科學, 2011, 33(6): 57-62.

[11] 王成偉. 帶有參數的三次三角多項式樣條曲線[J].北京服裝學院學報(自然科學版), 2008, 28(3): 50-55.

[12] 韓旭里. 基于四點分段的一類三角多項式曲線[J].中國圖象圖形學報, 2002, 7(10): 1063-1066.

[13] 吳曉勤. 基于三點分段的三角多項式樣條曲線[J].工程圖學學報, 2005, 25(2): 101-105.

[14] 嚴蘭蘭. 帶形狀參數的三角曲線曲面[J]. 東華理工大學學報(自然科學版), 2012, 35(2): 197-200.

[15] 嚴蘭蘭, 梁炯豐. 一種類四次三角樣條曲線[J]. 計算機工程與應用, 2010, 46(31): 165-168.

Five-and Six-Order Trigonometric Spline Curves

Yan Lanlan1,2, Han Xuli2, Huang Tao1
(1. College of Science, East China Institute of Technology, Nanchang Jiangxi 330013, China 2. School of Mathematics and Statistics, Central South University, Changsha Hunan 410083, China)

Using trigonometric functions, two groups of functions with parameters are constructed, which consist of six and seven functions respectively. The properties of the two groups of functions are analyzed. Based on them, two kinds of new spline curves are defined, which have the same structure with quintic and sextic B-spline curves respectively. The new curves not only inherit the basic properties of B-spline curve, but also have some new advantages. For example, when the knot points are equidistant, the new curves can reach C5continuous at the knot points, and the shape of the new curves can be adjusted by changing the value of the shape parameter with the control points unchanged. In addition, the methods of making the new curves interpolating the first and end points of the control polygon, and the methods of constructing closed curves, etc, are given. The examples in the paper show the new method is correct and feasible.

curve design; trigonometric function; spline curve; shape parameter; continuity

TP 391

A

2095-302X (2014)02-0200-08

2013-05-22；定稿日期：2013-08-29

國家自然科學基金資助項目（11261003，11271376，60970097）

嚴蘭蘭（1982-），女，湖北浠水人，講師，博士研究生。主要研究方向為計算機輔助幾何設計。E-mail：yxh821011@aliyun.com