基于直線平行垂直關系美化三維線框模型

何 波， 高滿屯， 王淑俠

（西北工業大學機電學院，陜西 西安 710072）

基于直線平行垂直關系美化三維線框模型

何 波， 高滿屯， 王淑俠

（西北工業大學機電學院，陜西 西安 710072）

針對計算機線圖解釋中直線間幾何關系可能存在不準確，從而出現視覺表達問題的不足，研究了基于直線平行垂直關系美化三維線框模型方法。首先，計算正視投影空間中三維線框模型中棱線方向矢量并選擇基準棱線；然后，采用直線間平行垂直約束對線框模型中出現幾何錯誤的直線進行校正，重新選擇已校正棱線為基準棱線重復上述操作；最后根據新的棱線參數確定三維線框模型頂點新坐標。通過算例結果表明，該方法能夠有效地解決線框模型中出現的平行垂直幾何問題，達到線框模型視覺上的美化。

線圖解釋；線框圖模型；幾何結構；美化

在工程設計的概念設計階段，設計者經常畫出立體線圖（草圖），且需要反復對設計進行修改。目前，具有強大功能的CAD系統只能對設計的詳細設計過程提供很大的幫助，而處理草

圖的能力極弱，也不能直接將線圖轉換為三維物體結構信息，不便于在工程設計的概念設計階段使用。

隨著科學技術的發展，人機之間用圖形進行通訊日益受到重視，在許多場合顯示出其重要性。為使計算機能“看”懂物體投影線圖，需要研究計算機解釋投影線圖的機理。計算機分析、處理和理解線圖的研究成果可用于互聯網、CAD系統中的人機通訊接口、逆向工程及計算機視覺系統等領域，能縮短圖形輸入時間，減輕人-機通訊中“人”的工作量。

線圖解釋[1]是計算機視覺和模式識別的一個重要研究領域。線圖的解釋就是根據物體（或場景）的一幅或多幅投影圖像理解三維空間中的景物。對于高度進化的人類視覺而言，理解三維景物是一件比較容易的事情，但要用計算機來模擬這一過程，是一項極其困難的工作。

經過計算機解釋立體線圖后，從二維線圖恢復的三維物體線框圖模型，即使拓撲結構完全正確，恢復出的三維物體線框模型仍然可能存在幾何結構缺陷（如圖 1所示），而線框模型是構造三維物體實體模型的基礎。只有在保證三維物體線框模型拓撲和幾何結構正確的情況下才能得到正確的三維物體實體模型。

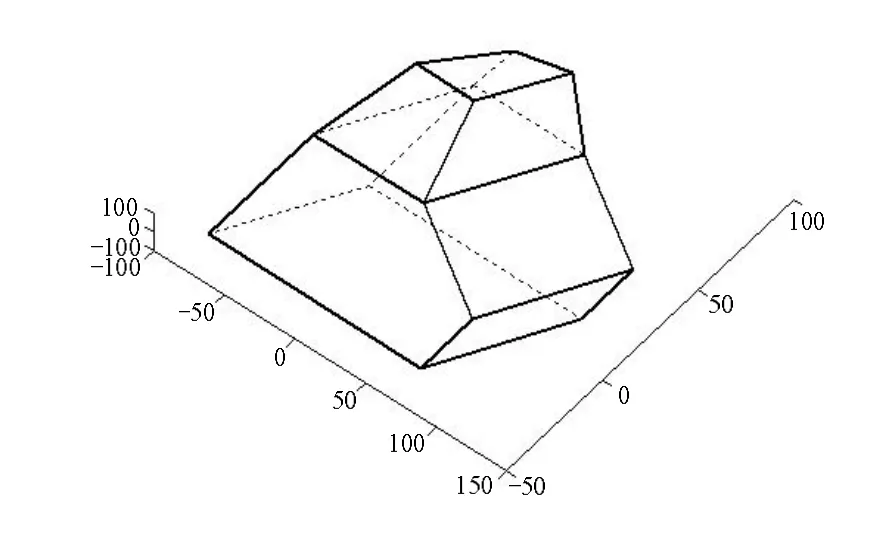
圖1 恢復的三維線框模型

從二維線圖恢復的三維線框模型經常出現如下一些問題[2-4]：①三維物體中應該平行的平面或直線未平行；②三維物體中應該垂直的平面或者直線不垂直；③三維物體上共平面的點實際上不共面；④三維物體的幾何結構中對稱的部分不完全對稱；⑤三維物體的幾何結構不符合力學性能、材料性能的要求，如壁厚不均勻，即面的距離不合適等；⑥三維物體中孔的位置不正確；⑦三維物體中兩個表面之間的夾角不符合要求。

Lipson和Shpitalni[5]提出了一個從單幅、不準確的二維線框草圖恢復三維物體結構的優化算法，線圖中的不準確包括頂點位置誤差和線圖不完整。但不足之處是初始值不宜選取，而且圖像中各種規則的提取比較困難。Company等[6]利用模擬退火技術進行優化，得到了局部最優解，優化結果能得到最可能符合人類視覺心理線圖。但是得到的最優解有可能是局部最優解而不是全局最優解。儲珺等[7]采用優化和迭代技術對線圖進行校正，使校正后的線圖是一個平面立體的正確投影，恢復的平面立體與原畫線圖表示的平面立體盡量接近，但這并不是一個合適的做法，實際上解釋線圖獲得三維物體是最終目標，而非三維物體的重投影盡量與原線圖一致。莫白聲[8]依據線圖空間結構中IE關系及FV關系采用了迭代方法對線圖進行了修正。但是其不足之處在于迭代運算中存在矩陣的降階問題，而且其所用方法最適用于對局部存在的誤差進行處理。Lee和Fang[9]研究了一種使用圖形上提取的立方體角信息及所標識面信息作為初始信息的線圖恢復方法，這種方法非常精確而且效率很高，但同時該方法對初始值的精確要求很高，如果采用了不準確的初始信息，則恢復的三維模型會出現扭曲變形，達不到線圖解釋基本目的。

現有線圖解釋優化方法雖然能從線圖中恢復平面立體三維結構，但仍會出現恢復的平面立體有時不符合人類視覺感受，不具備美化效果。若線圖解釋中考慮幾何元素之間的相對位置關系和度量關系，則線性系統將轉化為非線性系統，使問題變得更復雜。所以本文提出新的觀點，將計算機線圖解釋分為兩步，首先進行傳統意義上的三維恢復，然后采用本文提出的美化方法對線框圖進行后期處理，得到人類視覺感官上可以接受的三維線框模型。

1 基于直線關系美化三維物體

1.1 三維物體線框模型美化算法

本文主要基于棱線之間的平行、垂直、相交關系美化三維物體的線框模型。基于直線平行、垂直關系的三維線框模型美化算法流程圖如圖2所示。

1.2 棱線之間的平行性約束判斷及修正

從二維線圖到三維物體線框模型中的過程中，二維線圖上平行的直線，在三維物體線框模型中理論上應該是平行或異面，而實際模型中，棱線都是一些線段，而三維物體上的線段數量又

在可計算的范圍之內，因此異面直線的問題在實際應用上可以不用考慮。三維物體線框模型中棱線之間的平行性約束，由于誤差、誤差傳播以及二維線圖中的誤差等原因，可能沒有滿足或者沒有精確滿足，因此，三維物體線框圖中的棱線平行性約束有些需要修正。

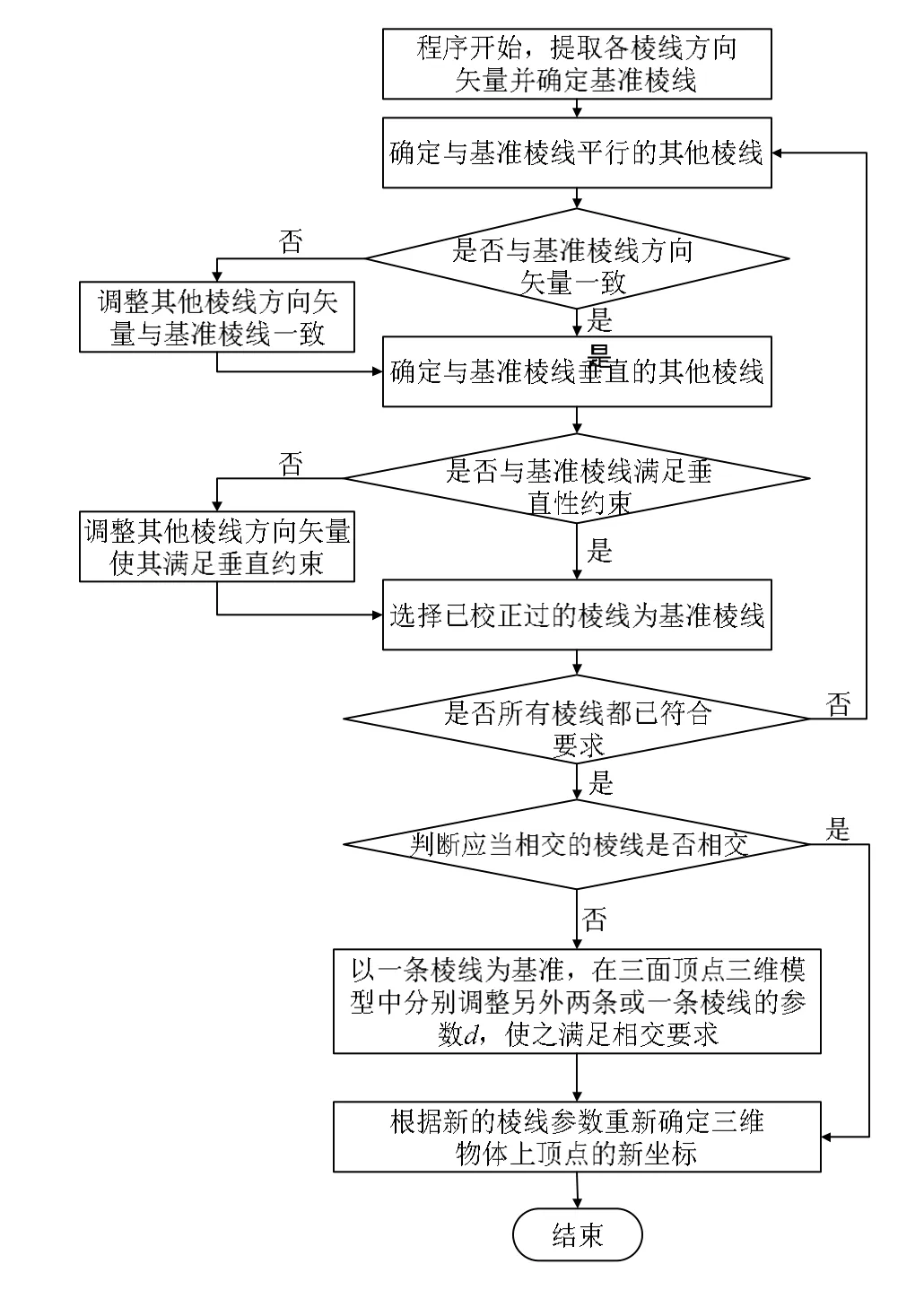
圖2 算法流程圖

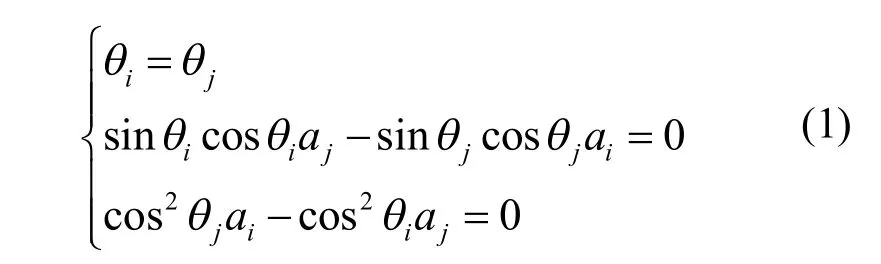
式(1)中各個參數均為正軸測投影下三維直線法線式表達式[1]中的參數，其中ρ為空間直線的投影直線的法線長，θ表示為投影直線夾角，aj與 dj為空間直線推導中的參數。

根據式(1)，棱線平行所滿足的約束條件為：

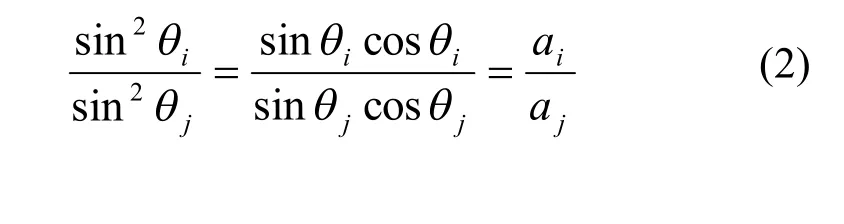
為簡化形式，令：

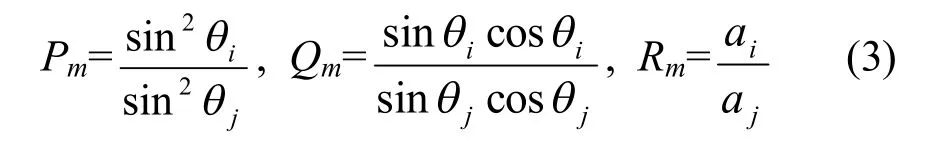
根據三維物體線框模型的數據進行判斷，驗證線框模型中應該平行的棱線是否平行，然后根據平行性約束，對不滿足平行性的棱線進行修正。如圖3所示，該線框模型中一共有12個頂點，18條棱線（其中有平行棱線15對）。先獲得的18條棱線的參數和12個頂點的z坐標值。

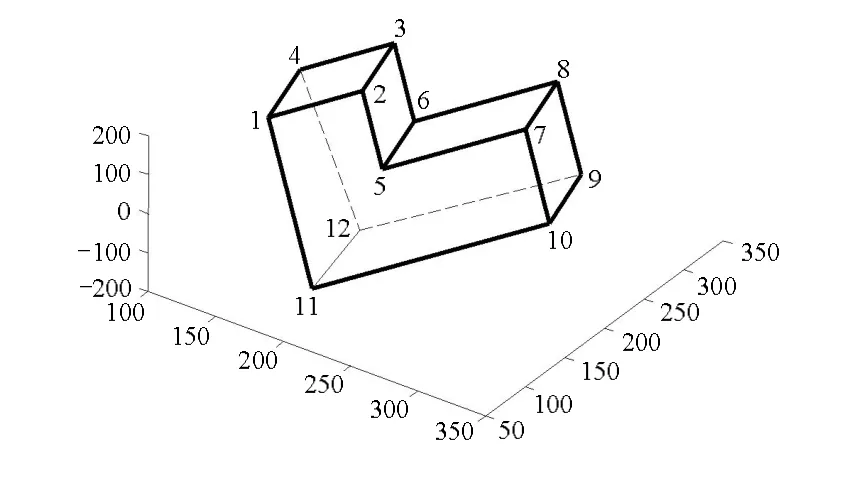
圖3 恢復的三維物體線框模型

1.3 棱線之間的垂直性約束判斷及修正

由于誤差、誤差傳播以及二維線圖中的誤差等原因，三維物體線框模型中棱線之間的垂直性約束可能沒有滿足或者沒有精確滿足。因此，三維物體線框圖中的棱線垂直性約束有些需要修正。

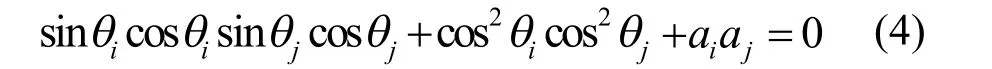
如圖3所示，以三面頂點1為例來分析，屬于頂點1的三條棱線中，若與不垂直，以棱線為基準棱線，因此需要調整 L(1,11)的方向矢量。具體方法如下：

（1）設L(1,11)的方向矢量為 (sin2α ,-cosαsinα, - a)，其中a和α為需要重新確定的未知參數；

（3）求解方程組得便可得 a和α的數值，即為L(1,11)所需調整數值；其他棱線之間垂直性的判別和修正類似。

1.4 棱線相交性判斷與修正

三維物體線框模型中的棱線經過利用垂直性和平行性約束進行調整其方向矢量后，有可能就不滿足棱線的相交性約束了，因此，經過調整以后的三維物體線框模型需要進一步判斷和修正三維物體線框模型上應該相交棱線是否仍然相交。經過上面兩步調整之后，各條棱線的方向矢量已經確定，棱線是否相交只與棱線參數d有關。因此，如果棱線不滿足相交的約束，只需調整棱線的參數d。空間兩條棱線相交的約束條件為：

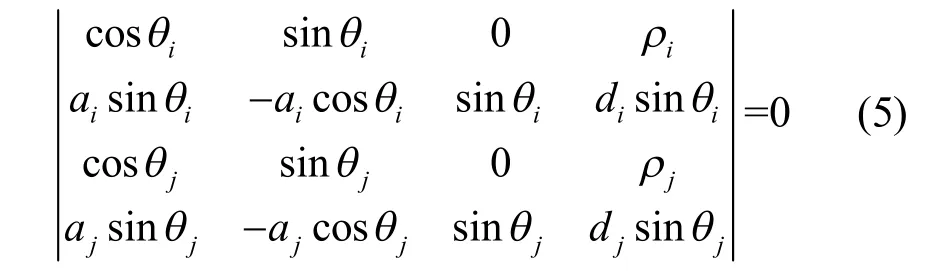
其中 ai和 aj為已知，如果兩條棱線不相交，則固定基準棱線不動，調整另外一條棱線的參數d。

調整過棱線的方向矢量之后，棱線對之間滿足了平行性與垂直性約束，但各棱線對之間可能不再滿足相交的約束條件。因此，需要在不改變棱線方向矢量的條件下調整棱線的空間位置。由空間直線的方程：

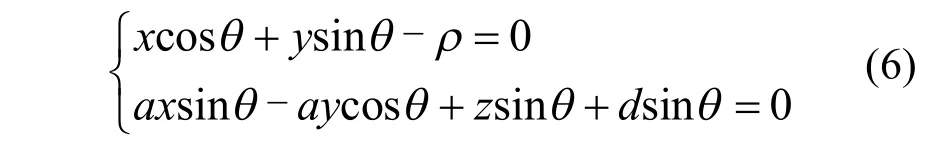
式中，ρ、sinθ、cosθ為從二維線圖中所獲得的已知信息。又由于空間棱線的方向矢量

為已經得以確定，參數 a已經完全確定。因此，調整三維物體上棱線的位置只能調整參數d。

具體調整方法：任選一條棱線為基準棱線，如選擇棱線L(1,2)為基準，即L(1,2)的參數不變，根據棱線 L(1,2)與棱線 L(1,4)的相交約束，即根據式(5)，獲得 d1的值。同理，獲得與棱線 L(1,2)相交的所有棱線的d值；再選已經確定d值的棱線為基準棱線，根據棱線對之間的相交約束獲得與其相交所有棱線的d值；依次調整三維物體上的其他所有棱線的位置。

1.5 三維物體上頂點坐標的重新確定

對一個三維物體線框模型經過上述各個過程的一系列調整之后，三維物體線框模型上各個頂點的位置也隨之發生了改變。因此，需要重新確定三維物體線框模型的所有頂點的位置。

三維物體上棱線的參數確定以后，確定三維物體上頂點的新位置就很容易了。根據三維物體最初始的頂點與棱線的拓撲關系，利用空間兩條直線相交求交點的方法可獲取頂點的新坐標。

2 算例演示

算例1圖4是從線圖解釋恢復的三維物體線框模型。根據人類視覺習慣和工程實際要求，該三維物體線框模型中的棱線有些應該滿足垂直性和平行性約束條件，但恢復出的三維物體線框模型沒有滿足這些條件，如L(1,2), L(1,3), L(1,4)顯然與對應棱線不平行而且相互之間也未垂直。因此需要對恢復的三維物體線框模型進行美化。采用本文方法美化后的三維物體線框模型，如圖5所示。從圖中可以看出，采用本文美化方法達到線框模型視覺上的美化。

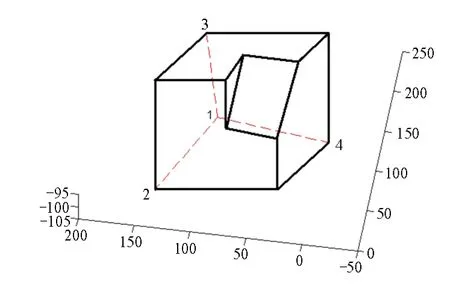
圖4 原三維物體線框模型

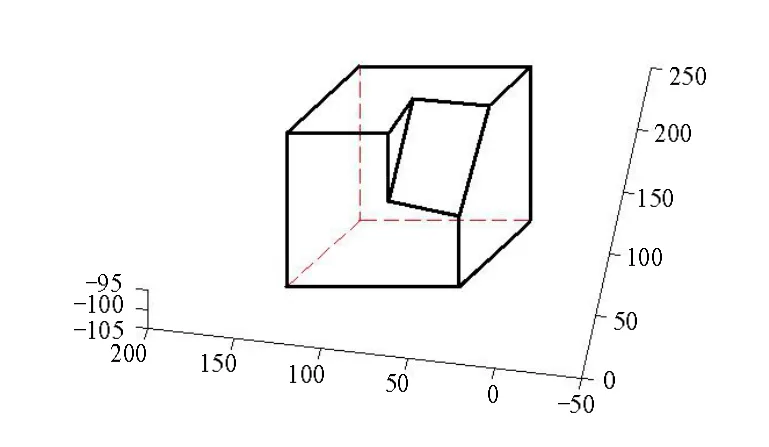
圖5 美化之后的三維物體線框模型

算例2圖6是從線圖解釋恢復的三維物體線框模型。由于線圖中一個節點的位置不正確，導致恢復的三維物體線框模型中一些棱線不滿足垂直性和平行性約束條件。采用本文方法美化后的三維物體線框模型如圖7所示。從圖中可以看出，采用本文美化方法達到線框模型視覺上的美化。

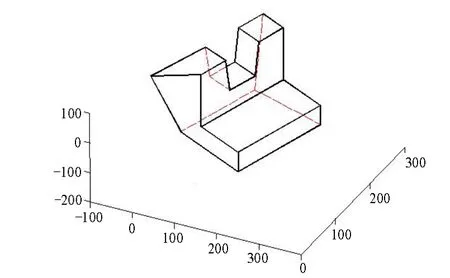
圖6 原三維線框模型

圖7 美化之后的三維物體線框模型

3 結 論

提出了基于直線平行約束、垂直約束、相交關系美化三維物體線框模型的算法。通過大量美化三維物體的實踐，作者認為，在美化三維物體時，利用的關系順序最佳為：平行→垂直→平行→…→平行→垂直→相交。采用本文美化方法美化有誤差的三維物體線框模型，獲得了符合實驗目標的三維物體線框模型，達到線框模型視覺上的美化。

[1] 高滿屯, 儲 珺, 董黎君. 計算機解釋立體線圖的方法與實踐(2009)[M]. 西安: 西北工業大學出版社, 2009: 171-184.

[2] Varley P A C, Martin R R, Suzuki H. Can machines interpret line drawings?[C]//Sketch-Based Znterfaces and Modeling 2004: Eurographics Symposium Procedings. Aive-la-Ville, Switzerland: Eurographics, Association, 2004: 107-116.

[3] 高滿屯, 儲 珺, 董黎君. 線圖解釋研究綜述[J].工程圖學學報, 2006, 27(5): 1-11.

[4] 儲 珺. 從單幅畫隱線立體線圖恢復平面立體三維結構的研究[D]. 西安: 西北工業大學, 2005.

[5] Lipson H, Shpitalni M. A new interface for conceptual design based on object reconstruction from a single freehand sketch [J]. CIRP Annals-Manufacturing Technology, 1995, 44(1):133-136.

[6] Company P, Contero M, Conesa J, Vicent A P. An optimisation-based reconstruction engine for 3D modelling by sketching [J]. Computer Aided Design, 2004, 28(6): 955-979.

[7] 儲 珺, 高滿屯, 陳國定. 基于迭代技術的有誤差單幅線圖的計算機解釋[J]. 模式識別與人工智能, 2005, 18(5): 615-620.

[8] 莫白聲. 平面立體線圖解釋的誤差分析和誤差修正研究[D]. 南昌: 南昌航空大學, 2007.

[9] Lee Y T, Fang Fen. 3D reconstruction of polyhedral objects from single parallel projections using cubic corner [J]. Computer Aided Design, 2011, 43(8):1025-1034.

Beautification of Wireframe Model of Three-Dimensional Objects Based on Parallel and Vertical Linear Relationship

He Bo, Gao Mantun, Wang Shuxia
(College of Electromechanical, Northwestern Polytechnical University, Xi′an Shaanxi 710072, China)

In order to solve the problem that errors may exist in the geometrical interpretation of the relationship between the lines and thus result in the inadequacy in visual expression,a method is developed on parallel and vertical linear relationship for beautifying the wireframe model of three-dimensional objects. Firstly, the ridge direction vector of the three-dimensional wireframe models in the face projection space is calculated and a benchmark ridge is chosen; then geometric errors appearing in wireframe model are corrected by the parallel and vertical constraint of the linear relationship, the corrected ridge is reselected as the new benchmark and a repeatition of the operation is conducted. Finally, the new coordinates of the vertices of the three-dimensional wireframe models are calculated according to the new ridge parameter. The numerical example shows that the proposed methods can effectively solve the parallel and vertical geometric problems in the wireframe model to beautify the wireframe model.

line drawing interpretation; wireframe model; geometry structure; beautification

TP 391.41

A

2095-302X (2014)03-0325-05

2013-11-08；定稿日期：2014-01-23

國家自然科學基金資助項目（51105310；513101435）

何 波（1986-），男，陜西寶雞人，碩士。主要研究方向為計算機圖形學。E-mail：heyu1743@163.com

高滿屯（1962-），男，山西襄汾人，教授，碩士。主要研究方向為投影理論、圖形學、計算機視覺、幾何學。E-mail：gaomant@nwpu.edu.cn