高速列車引起的深水橋墩流固耦合的振動分析

盧華喜，李 軍，周葉威，梁平英

（華東交通大學土木建筑學院，江西 南昌 330013）

高速列車引起的深水橋墩流固耦合的振動分析

盧華喜，李 軍，周葉威，梁平英

（華東交通大學土木建筑學院，江西 南昌 330013）

為研究水體對橋墩結構振動特性的影響，以ANSYS為計算平臺，建立了橋墩-水流固耦合有限元模型，計算了不同幾何尺寸和淹沒比情況下橋墩的自振頻率，分析了橋墩在高速列車作用下，不同水深對其振動特性的影響。分析后得出結論：當水體深度小于墩高50%時，橋墩的自振頻率降低不明顯；當水體高度大于墩高50%時，橋墩自振頻率出現明顯降低。高速列車作用下，橋墩墩頂縱向位移出現極值的時間，隨淹沒比的增加向后推遲；橋墩墩頂縱向加速度隨淹沒比的增加而增加。因此，高速列車作用下，水體對于涉水鐵路橋梁橋墩的自振與動力振動特性有著明顯的影響，且這種影響不可忽視。

自振頻率；激振力；流固耦合；縱向位移；縱向加速度；

當前涉水鐵路橋梁的建設，基本都是在向深水和大跨度發展，在已建和在建的涉水鐵路橋梁中，橋墩入水深度最深已達168 m。當前的涉水鐵路橋梁設計中，大部分將橋墩所處的環境視為靜態環境來考慮，即將橋墩周圍的流體考慮為空氣而不是水體［1］。但實際上，涉水鐵路橋梁的橋墩特別是深水橋墩都是浸沒在不同深度的水中，在高速列車的作用下，這些處于深水中的橋墩會發生一定振動和變形，并引起周圍水體的晃動，水體又以動水壓力的形式反作用于橋墩，改變橋梁墩身的振動和變形狀態，這種作用與反作用伴隨著高速列車的通過。橋墩作為橋梁的下部承載結構，對整個橋梁的安全和穩定起著至關重要的作用。因此，深入研究橋墩在考慮水體的影響下自振與動力振動特性，對橋墩乃至整座橋梁結構安全和穩定是至關重要的。本文主要分析在高速列車作用下，橋墩與外部水體流固耦合的振動問題，使用ANSYS有限元軟件建立橋墩-水流固耦合有限元模型，分析得出不同水深情況下橋墩的自振和動力振動特性。

1 有限元模型的建立

為了研究水體對橋墩振動特性的影響程度，本文選用幾種幾何尺寸不同的橋墩模型進行模擬分析，橋墩的材料屬性取彈性模量E=3.0×1010Pa，泊松比ν=0.2，密度ρ1=1 460 kg·m-3，且橋墩底部為固定端，梁體對墩頂面有一定的約束作用，故墩頂施加彈性約束。由于橋墩周圍水域的寬度相對橋墩可以認為是無限大的，所以在建立水體模型時，取水域半徑為橋墩界面半徑的5倍較為合適［2］，水體的材料屬性取密度ρ2=1 000 kg·m-3，水中的聲速取V=1 460 m·s-1，吸收系數β=0.8。

利用ANSYS有限元軟件中的Solid45單元來模擬實體橋墩部分，Fluid30流體單元來模擬水體部分。當KEYOPT（2）＝0時，流體單元與結構單元接觸，可建立與橋墩結構相接觸的水體模型；當KEYOPT（2）＝1時，流體單元與結構單元沒有接觸，可建立沒有與橋墩結構直接接觸的水體模型。Fluid30單元還必須和Fluid130單元聯合使用，用Fluid130單元構造包圍Fluid30單元的無限外殼，此外殼被認為是第二階吸收邊界。當壓力波（水波）到達這個邊界時，將會被吸收，然后以最小的反射吸收到流體域內［3-9］。選擇Fluid30流體單元作為水體模型，模擬與橋墩結構流固耦合的模態頻率分析時，應該滿足以下假定：假設水體是可壓縮的、非粘性的、無平均流量且不考慮水體的熱傳導性。模型建立完成后，在橋墩與水體的接觸面上施加FSI流固耦合標簽，即可實現流固耦合，在水體外圍施加壓力為零的邊界條件。流固耦合有限元模型和模型截面類型分別見圖1、圖2。

圖1 橋墩-水流固耦合有限元模型Fig.1 The finite element model of bridge pier-water fluid-solid interaction

2 水深對橋墩自振特性的影響

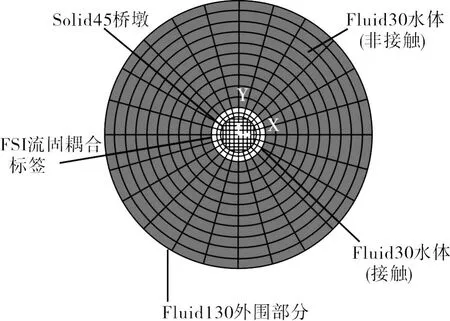
圖2 模型截面類型Fig.2 The section type of model

為了分析只考慮不同水深對橋墩自振特性的影響，故選用不同半徑和墩高不同的橋墩模型進行模擬計算，這樣可以排除橋墩尺寸對結果的影響，以及可以得到較為普遍的結論。所以，取①橋墩半徑R1=1.0 m，橋墩高度分別取H=10，20，30，40，50 m；② 橋墩半徑R1=2.0 m，橋墩高度分別取H=60，70，80，90，100 m。根據各種材料的屬性，以及橋墩的幾何尺寸、流體域的大小建立ANSYS有限元模型。為突出研究水深對橋墩自振頻率的影響，選橋墩淹沒比h/H（水深/墩高）分別為0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0。對模型進行模態化分析，可以得到橋墩在不同淹沒比下的自振頻率，見表1和表2。

表1 R1=1.0 m時橋墩自振頻率Tab.1 The natural frequency of bridge piers when R1=1.0 m Hz

表2 R1=2.0 m時橋墩自振頻率Tab.2 The natural frequency of bridge piers when R1=2.0 m

由表1和表2可以看出，不同橋墩尺寸下，橋墩自振頻率隨著淹沒比的增加呈減小趨勢，與橋墩半徑和高度無關。當橋墩淹沒比h/H＜0.5時，橋墩自振頻率無明顯減小，最大減小幅度為0.5%，可以忽略不計；當橋墩淹沒比h/H＞0.5時，橋墩自振頻率出現明顯減小，其減小幅度隨著淹沒比的增加而增加；當橋墩淹沒比h/H=1.0即橋墩被完全淹沒時，其自振頻率最小，相對無水情況下的自振頻率，最大減小幅度達到16.5%，故不可忽略。橋墩自振頻率變化曲線，見圖3和圖4。

圖3 R1=1.0 m時橋墩自振頻率變化曲線Fig.3 The curve of the natural frequency when R1=1.0 m

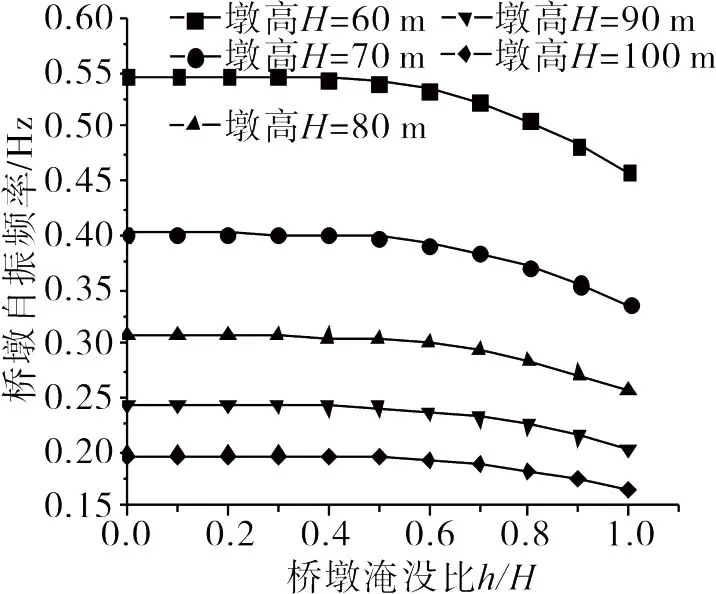
圖4 R1=2.0 m時橋墩自振頻率變化曲線Fig.4 The curve of the natural frequency when R1=2.0 m

3 橋墩的動力振動特性分析

3.1 縱向激振力及模型加載［10］

本文主要分析車速為120 km·h-1時，車橋結構體系對橋墩的縱向激振力引起橋墩-水流固耦合的振動問題，縱向激振力時程圖，見圖5。這種激振力分布作用在墩頂上，根據圣維南原理，可將分布力等效為集中荷載作用在墩頂的中心，橋墩-水流固耦合模型加載圖，見圖6。

圖5 激振力時程Fig.5 Time history curve of exciting force

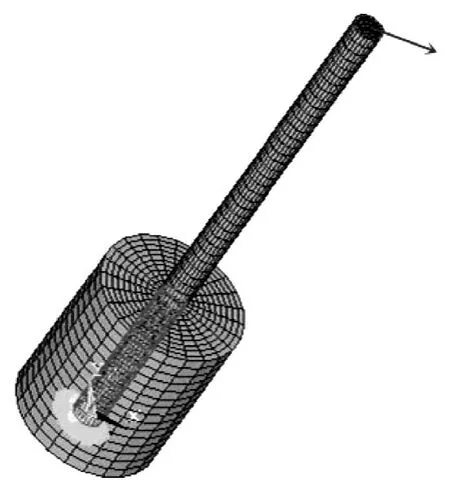
圖6 模型加載圖Fig.6 The picture of model loading

3.2 水深對墩頂縱向位移的影響

為了研究水體對橋墩墩頂縱向位移的影響，選用橋墩的幾何尺寸分別為①橋墩半徑R1=2.0 m，墩高H=90 m，100 m，②橋墩半徑R1=2.5 m，墩高H=90 m，100 m。由第3結可以看出，當橋墩淹沒比h/H=1.0時，水體對橋墩自振頻率的影響最為突出，故橋墩的淹沒比h/H分別取0，1.0即無水和滿水，這樣有利于分析和對比，橋墩墩頂縱向位移的時程曲線，見圖7、圖8。

圖7 位移時程Fig.7 Time history curves of displacement

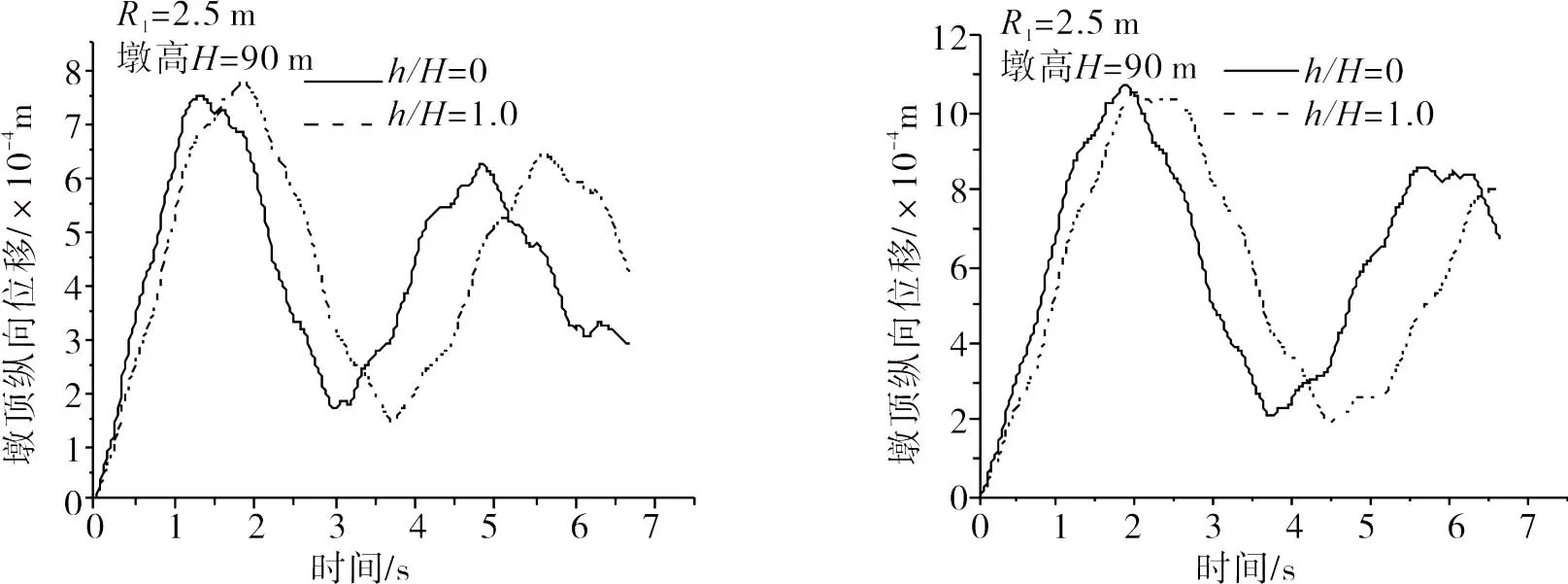
圖8 位移時程Fig.8 Time history curves of displacement

由圖7和圖8可以看出，在高速列車作用下，同一墩高時，墩頂縱向位移隨著半徑的增加而減小；同一半徑時，墩頂縱向位移隨著墩高的增加而增加；同一半徑和墩高時，墩頂縱向位移最大值和最小值，隨著淹沒比的增加向后延遲。

3.3 水深對墩頂縱向加速度的影響

為了研究水深對墩頂縱向加速度的影響，橋墩模型尺寸同4.2節。在橋墩模型頂部施加縱向激振力，可以分析得到墩頂縱向加速度的大小，其時程曲線，見圖9、圖10。

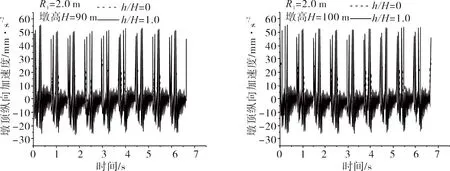
圖9 加速度時程Fig.9 Time history curves of acceleration

圖10 加速度時程Fig.10 Time history curves of acceleration

由以上各圖可知，在高速列車作用下，同一墩高時，墩頂縱向加速度的大小隨半徑的增大而減小；同一半徑時，墩頂縱向加速度的大小隨墩高的增加呈減小趨勢，減小幅度并不明顯；同一半徑和墩高時，墩頂縱向加速度的大小隨淹沒比的增加而增加。這是由于高速列車作用產生的激振力引起橋墩的振動，橋墩將這種振動部分傳遞給周圍水體，并引起水體的晃動，水體又以動水壓力的形式反作用于橋墩，改變橋梁墩身的振動和變形狀態。

4 結語

本文建立了不同幾何尺寸和橋墩淹沒比情況下橋墩-水流固耦合有限元模型，分析了水深對橋墩自振特性的影響；通過在墩頂施加縱向激振力，研究了不同淹沒比情況下，橋墩的動力振動特性。并得出以下結論：①當橋墩淹沒比h/H＜0.5時，水體對橋墩自振頻率的影響十分微小，可以忽略不計。②當橋墩淹沒比h/H≥0.5時，橋墩自振頻率隨著橋墩淹沒比的增加出現明顯降低，最大降低幅度達到16.5%。③當橋墩淹沒比h/H=1.0即橋墩被完全淹沒時，橋墩自振頻率達到最小值，且橋墩自振頻率隨淹沒比的變化規律與橋墩幾何尺寸無關。④墩頂縱向位移出現最大值和最小值的時間，隨著橋墩淹沒比的增加向后延遲，且與橋墩幾何尺寸無關。⑤墩頂縱向加速度隨淹沒比的增加呈增大的趨勢，且與橋墩幾何尺寸無關。

[1]屈愛平,高淑英.梁-橋墩-樁基礎的動力特性研究[J].西南交通大學學報,2001,36(6):641-644.

[2]柳春光,齊念.考慮流固耦合作用的深水橋墩地震響應分析[j].防突減災工程學報,2009,29(4):433-437.

[3]楊萬理,李喬.深水橋墩流固耦合下的自振特性研究[J].四川建筑科學研究,2012,38(3):164-170.

[4]錢若軍,董石麟,袁行飛,等.流固耦合理論研究進展[J].空間結構,2008,14(1):3-15.

[5]楊吉新,雷凡,李昆,等.水下橋墩結構的振動分析[J].世界橋梁,2009,(3):40-42.

[6]崔濤.高速列車流固耦合振動及運行安全性研究[D].西南交通大學,2011.

[7]賴偉,王君杰,韋曉,等.橋墩地震動水效應的水下振動臺試驗研究[J].地震工程與工程振動,2006,26(6):164-171.

[8]傅作新.結構與水體的動力相互作用問題.[J].水利水運科學研究,1982,(2):104-119.

[9]高芒芒,李永強,許北軍,等.高速列車作用下的蕪湖長江大橋車橋耦合振動分析[J].中國鐵道科學,2001,22(5):34-40

[10]羅文俊,雷小燕,練松良,等.車輛-高架橋耦合系統豎向振動分析車輛軌道新模型[J].華東交通大學學報,2013,30(2):1-8

Vibration Analysis of Deepwater Bridge Pier Based on Fluid-Solid Interaction Caused by High-speed Train

Lu Huaxi,Li Jun,Zhou Yewei,Liang Pingying
(School of Civil Engineering and Architecture,East China Jiaotong University,Nanchang 330013,China)

To research the effect of water on the vibration characteristics of bridge pier structure,this study built a bridge pier-water fluid-solid interaction finite element model based on the computing platform of ANSYS,calcu?lated the natural frequency of the bridge pier at different water depths,and then analyzed effects of water depths on the bridge pier vibration characteristics under the role of high-speed train.The conclusions drawn from the analysis were:when the water depth was less than 50%height of the pier,the natural frequency of bridge pier did not decrease significantly;when the water depth was higher than 50%height of the pier,the natural frequency of bridge pier reduced obviously;under high-speed train,with the increase of the water height the time of the longitu?dinal displacement extreme appeared lingeringly and the longitudinal acceleration of the pier increased.There?fore,it concludes that water structure has obvious effects on the static and dynamic vibration characteristics of bridge pier,which can not be neglected.

natural frequency;exciting force;fluid-solid interaction;longitudinal displacement;longitudinal acceler?ation

U443.22

A

1005-0523（2014）02-0026-06

2013-09-20

國家自然科學基金項目（50968007）；江西省青年科學家培養對象計劃（2010DQ01800）

盧華喜（1976—），男，副教授，博士，研究方向為地基—基礎—部結構動力機組作用研究。