高速弓網耦合系統動態仿真研究
劉仕兵,汪 媛
(華東交通大學電氣與電子工程學院,江西 南昌 330013)
高速弓網耦合系統動態仿真研究
劉仕兵,汪 媛
(華東交通大學電氣與電子工程學院,江西 南昌 330013)
采用歐拉-伯努利梁結構的接觸網和受電弓的二質量塊模型建立了弓網垂直耦合動力學模型,通過拉格朗日方程推導出弓網系統運動微分方程組,并利用Newmark法編寫數值仿真程序,在給定的條件下,討論不同速度下弓網耦合系統的動態性能。采用MATLAB對高速受電弓與接觸網的相互作用進行仿真并對結果進行分析,為研究不同速度下受電弓與接觸網參數的優化奠定基礎。
接觸網;受電弓;數值仿真;接觸壓力
高速運行的電力機車通過受電弓與接觸網滑動接觸取得電能,受電弓與接觸網可靠地接觸是保證高速受流的重要條件,電氣化鐵路要實現高速,就必須解決接觸網與受電弓的相互匹配及對速度的適應問題。
本文建立基于二元弓的弓網耦合系統垂向動力學模型,利用Newmark法編寫了數值仿真程序;研究了弓網動態性能與列車運行速度之間的關系,為優化弓網系統的結構參數提供依據。
1 接觸線振動微分方程
接觸網是沿鐵路線上空架設的空間架空線結構,主要由承力索、接觸線、定位裝置、支柱和基礎幾部分組成[1],接觸網是具有一定抗彎剛度的線索結構,數值模擬仿真中的接觸網有限元模型采用的是歐拉-伯努利梁來模擬[2],其中接觸線的運動方程為
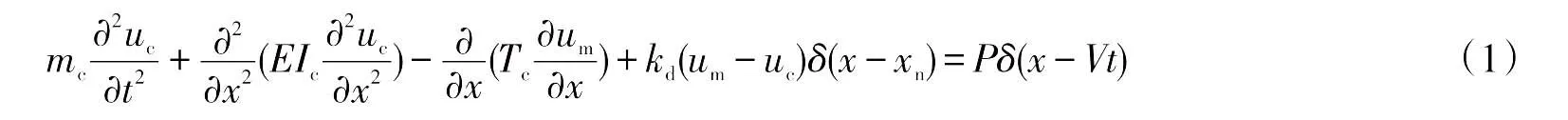
式中:mc,uc,EIc,Tc分別代表接觸線的單位質量,位移,抗彎剛度和張力;δ為沖擊函數;um是承力索的位移;kd是吊弦剛度;xn是吊弦離運動點處的距離;P是受電弓對接觸網的接觸壓力;x是列車運行的位置;t是運動時間;V是列車運行速度。
承力索的運動方程為
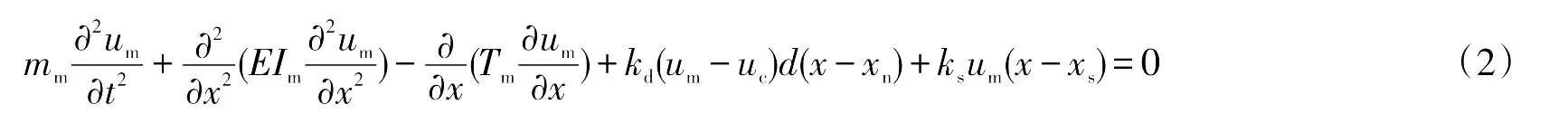
式中:mm,EIm,Tm分別代表承力索的單位質量,抗彎剛度和張力;kd是吊弦的剛度;ks表示支持裝置的等效剛度;xs是支柱處位移;xn是支柱點處到運動點處的距離。
2 受電弓質量塊模型
目前,研究受電弓的動力學特性常采用歸算質量模型,所謂歸算質量模型,就是利用動能等效原理將原結構簡化成幾個具有集總質量的模型[3]。本文采用二質量塊模型如圖1所示。
根據牛頓定律得到受電弓運動微分方程組表達式為[4]
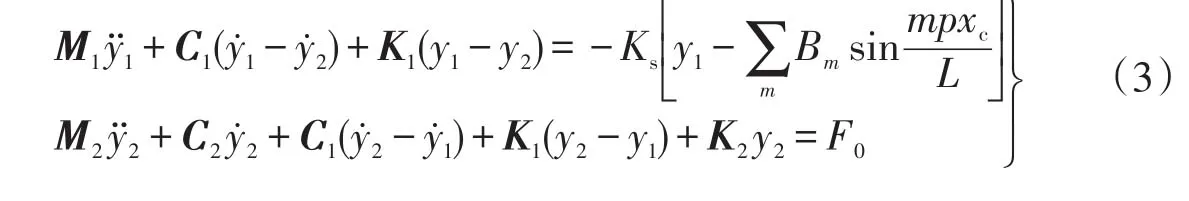
式中:M1,K1,C1,M2,K2,C2分別為受電弓模型中弓頭和框架的質量、剛度、阻尼矩陣;y1,y2分別為受電弓弓頭和框架的位移;Bm是接觸線第m階振幅;xc是接觸線的振動位移;F0為靜態抬升力。
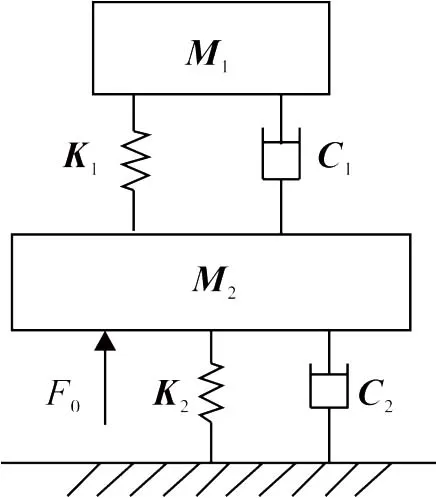
圖1 受電弓二質量塊模型Fig.1 Two mass model of pantograph
3 弓網系統耦合動力學模型
受電弓通過接觸剛度Ks與接觸網耦合在一起[5-6],圖2所示。其耦合通式為


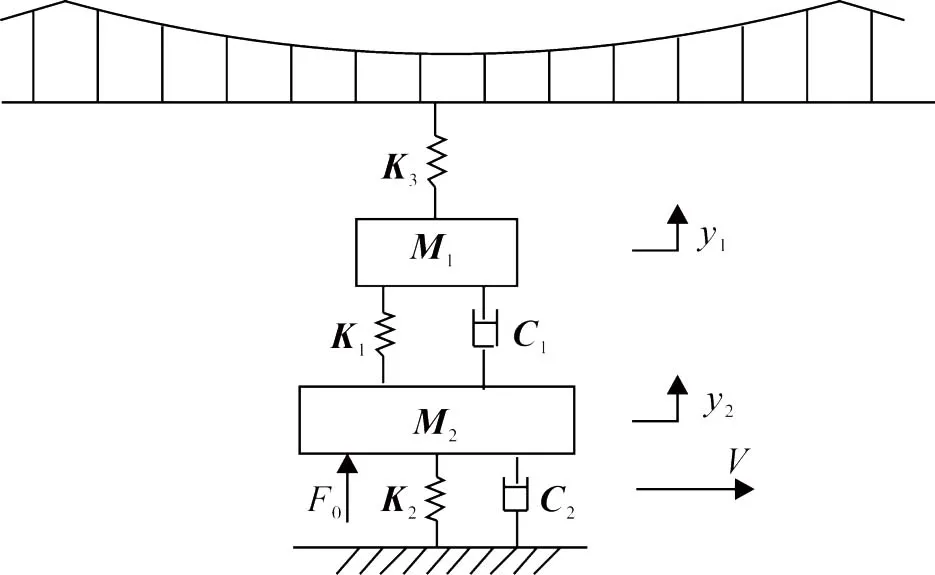
圖2 基于二元弓的弓網耦合系統模型Fig.2 Two mass model of pantograph’s Coupling system model
4 弓網耦合系統的數學模型的求解
求解振動微分方程的方法可分為解析法與數值法兩大類,解析法由于數學上的困難,通常只有某些簡單問題才能得到精確的解答,而對于多數復雜結構問題,還不能得到精確解。由于弓網系統的復雜性,進行弓網耦合振動分析,已遠遠超出了理論解析的范疇,必須要借助計算機進行數值仿真。
由前面的分析可知弓網系統的數學模型是非常復雜的,當受電弓在接觸線上通過時,其弓網系統的剛度矩陣隨之不斷地改變,其微分方程屬二階變系數常微分方程組,因此必須采用直接積分法求解,本文仿真算法采用Newmark法[7-8]。
1)仿真算法。Newmark法是由線性加速度法引申而來,其假設的速度、位移與加速度的關系如下


式中,α,β是參數,它們由積分精度和穩定性來決定的。仿真時取α=0.5,β=0.25是無條件穩定算法,時間步長Δt的大小不影響解的穩定性。帶入式(4)將取如下形式
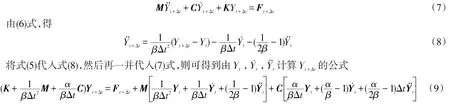

5 弓網動態性能仿真
1)接觸線動態抬升量。在仿真過程中,由于受電弓-接觸網的接觸耦合,引起接觸線的垂直方向運動。接觸線抬升量的變化以跨距為周期呈現一定的周期性,跨中的抬升量比定位點的抬升量大即在每跨內,抬升位移的最大值出現在跨中位置,最小值位于定位器附近。同時,還可以看到,接觸網跨中節點的抬升位移呈波動變化[10]。
2)不同運動速度下接觸力的變化。為研究受電弓以不同速度通過接觸網時各性能參數的變化,以下分別對160,200,250 km·h-13種速度工況進行計算。
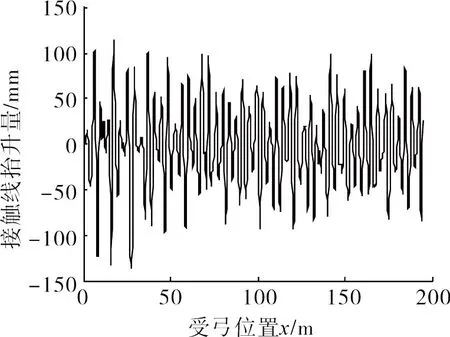
圖3 接觸線的抬升量變化曲線Fig.3 Changing curve of contact wire uplift
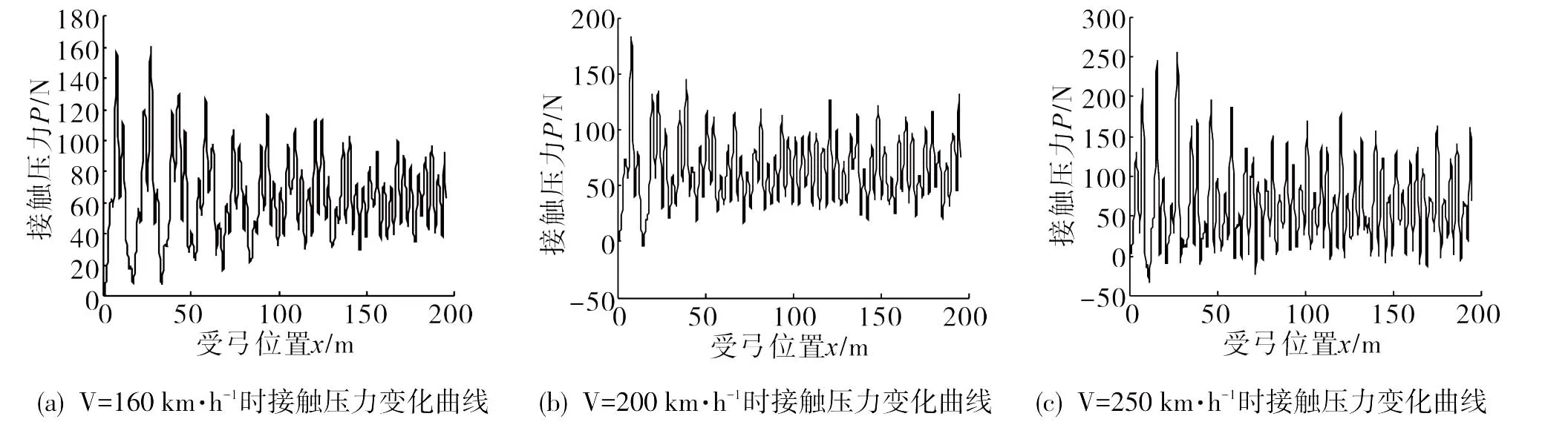
圖4 不同運行速度的接觸力變化曲線Fig.4 The contact force changes of different speed
從圖4可知,隨著運行速度的提高,接觸力的振蕩幅度明顯增大,當受電弓以200 km·h-1速度運行時,在1個位置出現了離線,而當運行速度提高至250 km·h-1時,弓網接觸力的振蕩更為劇烈,在多個位置出現了明顯的離線。由此可見,當受電弓運行速度高于200 km·h-1時,將直接影響弓網系統的安全。
6 結論
通過格拉格朗日方程推導出弓網系統振動微分方程組,利用Newmark法編寫了弓網數值仿真程序,對接觸線的動態抬升量和3種不同工況下的弓網動態接觸壓力進行了仿真及對比分析。研究結果表明:
1)接觸線的抬升量、接觸力以跨距為周期不斷變化,都隨著速度的增大而增大。
2)列車的運行速度對弓網動態性能起著直接的作用,隨著速度的提高,接觸壓力的波動幅度顯著增大,最小值減小,最大值增大,離線率增大。
3)接觸線動態抬升量最大值出現在跨中位置,最小值出現在定位點附近。
[1]于萬聚.高速電氣化鐵路接觸網[M].成都:西南交通大學出版社,2003:1-415.
[2]WU T X,BRENNAN M J.Basic analytical study of pantograph-catenary system dynamics[J].Vehicle System Dynamics,1988,30:443-456.
[3]POMBO J,AMBROSIO J,Pereira M.Influence of the aerodynamic forces on the pantograph-centenary system for high-speed trains[J].Vehicle System Dynamics,2009,47(11):1327-1347.
[4]于萬聚.高速受接觸網—受電弓系統動態受流特性研究[J].鐵道學報,1993,15(2):16-27.
[5]付秀通,詹婓生.輪/軌—弓/網系統耦合動力學數值模擬分析與試驗研究[J].鐵道學報,1998,20(3):25-32.
[6]張衛華,曹新文.高速受電弓—接觸網系統的動力學研究[J].西南交通大學學報,1991,26(l):105-111.
[7]翟婉明,蔡成標.機車—軌道輥合振動對受電弓—接觸網系統動力學的影響[J].鐵道學報,1998,20(1):32-38.
[8]周寧,張衛華.基于直接積分法的弓網耦合系統動態性能仿真分析[J].中國鐵道科學,2008,29(6):71-76.
[9]吳天行.接觸網的有限元計算與分析[J].鐵道學報,1996,18(3):44-48.
[10]衷路生,齊葉鵬,楊輝,等.PSO優化的LS-SVM在列車弓網系統的建模研究[J].華東交通大學學報,2012,29(3):1-6.
Dynamic Simulation Study on High-speed Pantograph-catenary System
Liu Shibing,Wang Yuan
(School of Electrical and Electronic Engineering,East China Jiaotong University,Nanchang,330013,China)
This paper uses the Euler-Bernoulli beam structure of catenary and two mass model of pantograph,es?tablishes the vertical coupling dynamics model of the pantograph catenary system,and derives pantograph-catena?ry system’s motion differential equations through the Lagrange equation.Using Newmark method,this paper also writes the simulation program,and in given conditions,discusses the dynamic properties of pantograph-catenary coupling system under different speeds.Using MATLAB,this paper simulates the interaction of high-speed panto?graph and catenary,analyzes the simulation results,and lays the foundation for pantograph and catenary's further parameters optimization under different high speeds.
cantenary;pantograph;numerical simulation;contact force
U225.3
A
1005-0523(2014)02-0068-04
2014-03-25
國家自然科學基金項目(11162002)
劉仕兵(1970—),男,副教授,碩士,主要研究方向為接觸網技術。

