基于擴展卡爾曼濾波的自適應混合估計算法

余輝榮 ，夏候凱順 ，葉景志 ，鄔依林 ，2

（1.華南理工大學 自動化科學與工程學院，廣州 510640；2.廣東第二師范學院 計算機科學系，廣州 510310）

多個目標的實時、精確跟蹤是無線傳感器網絡的重要應用和研究難點。隨著被跟蹤目標數量及其運動特征多樣性的增加，若要繼續保持有效跟蹤，則對于分布式傳感器節點的協同調度效率和定位算法的要求也同步上升。一個優良的定位算法必須具備自組織性、低能耗、高魯棒性和分布式計算等特點[1]。無線傳感器網絡中的目標跟蹤算法基本上分為直接通信法[2]、基于二進制探測的方法[3]、基于樹狀結構的方法[4]、基于簇狀結構的方法[5]、基于預測機制的方法[6]、基于粒子濾波的方法[7]、基于自適應機制的方法[8]和對偶空間轉換跟蹤方法[9]等。

傳統的最小二乘定位算法及常規的卡爾曼濾波定位算法是最常用的方法。前者具有收斂速度快、跟蹤及時等優點，但測量信號中的噪聲在融合后也被凸顯，導致定位軌跡波動較大；后者是一種高效率的自回歸濾波器，能夠從一系列不完全及包含噪聲的測量中，估計出動態系統的狀態[10]，抗觀測噪聲干擾能力強，其缺點是信號收斂速度較慢。因此，對于目標運動特性較復雜的情況 （如圖1所示），當運動速度發生突變時，運用單一的任一定位算法都無法達到快速且準確的追蹤。

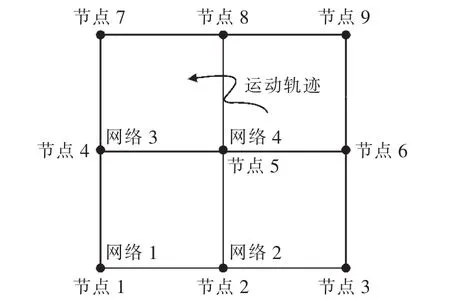
圖1 目標運動特性示意圖Fig.1 Schema of target motion characteristics

本文針對上述兩種算法的固有缺陷，提出了一種自適應的混合估計算法。該算法以基于單個觀測值的擴展卡爾曼濾波模型為基礎，結合收斂速度更快的最小二乘法對卡爾曼濾波估計進行修正，有效結合兩者的優點，以達到更優的跟蹤效果。

1 傳統定位算法分析

常規的TOA定位算法包括最小二乘法、基于泰勒展開的增量式算法、卡爾曼濾波算法等，其中以最小二乘法和卡爾曼濾波算法為主。

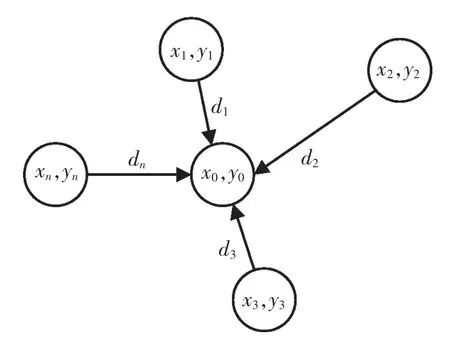
圖2 最小二乘原理圖Fig.2 Schema of least squares

1.1 最小二乘定位算法

在二維平面系統中，通過測得已知的n個傳感器節點（x1，y1），（x2，y2），（x3，y3），（xn，yn）…與目標的距離 d1，d2，…，dn，求得目標坐標（x0，y0）。根據圖 2 列出以下方程組：

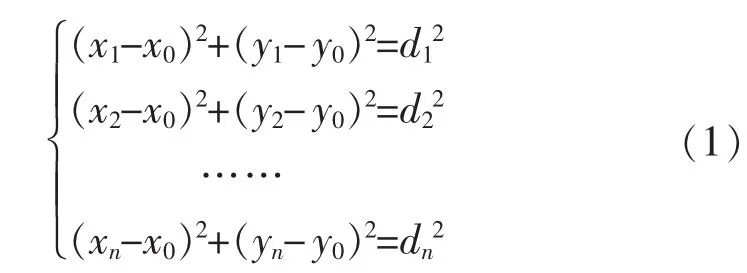
整理得：AX=B

其中：

采用最小方差的估計方法可得到坐標：

1.2 擴展卡爾曼濾波定位算法

對于多個跟蹤對象，假設各對象的線性離散系統模型如下：

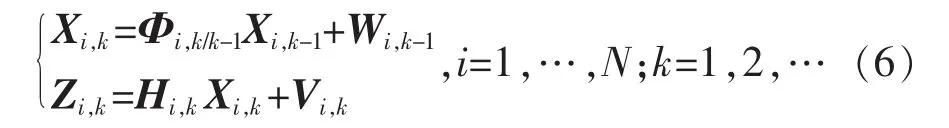
式中：N為網絡中目標個數；k為采樣時刻；Xi，k為k時刻被估計的n維系統狀態變量；Φi，k/k-1為k-1時刻到k時刻系統n維的狀態轉移矩陣；Zi，k為k時刻的m維觀測量；Hi，k為k時刻的m×n維量測矩陣，過程噪聲 Wi，k和觀測噪聲 Vi，k是均值為 0，符合高斯正態分布的白噪聲序列，其協方差矩陣分別為Qi，k-1和 Ri，k。

常規卡爾曼濾波遞推方法如下[11]：

在非線性的目標跟蹤系統中，要利用卡爾曼算法，將非線性過程圍繞當前的狀態估計利用泰勒級數展開方法進行近似線性化，再用卡爾曼濾波算法解決非線性系統的濾波問題，即擴展卡爾曼濾波算法（EKF）[12]。

1.3 單個觀測值的擴展卡爾曼濾波模型

將輪式移動機器人作為多目標跟蹤系統的移動目標，根據機器人的運動學方程建立濾波器模型的狀態方程：

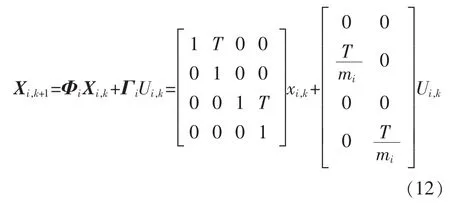
其中：第 i個移動機器人的狀態為 Xi=［xiνi，xyiνi，y］T，分別代表X軸、Y軸的坐標和速度；mi代表機器人的質量；T為采樣周期，此時狀態轉移矩陣是常數矩陣。

觀測方程 Zi，k=Hi，kXi，k的建立如下：

假設簇節點（xi，a，yi，a）在某一時刻 k 與目標 i之間的理論距離值為 di，a：

線性化可得：

其中：Zi，k=di，a，Xi，k=[xi，k，yi，k] 為 k 時刻第 i個機器人的坐標，觀測矩陣為

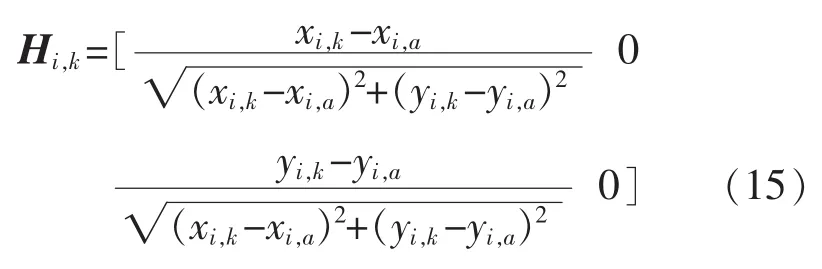
2 基于擴展卡爾曼濾波的混合估計算法

在多目標跟蹤應用系統中，由于目標運動特性及其跨越網格區域的多樣性，同時存在無線傳感器網絡因數據掉包而引起的觀測值丟失問題，觀測環境變得異常復雜。最小二乘定位算法受測量值噪聲影響大，而傳統的擴展卡爾曼濾波定位算法也存在一定程度的延時問題，使得網絡對于速度發生突變的目標的精確跟蹤變得困難，甚至出現丟失目標的嚴重后果。兩者的性能對比如表1所示。

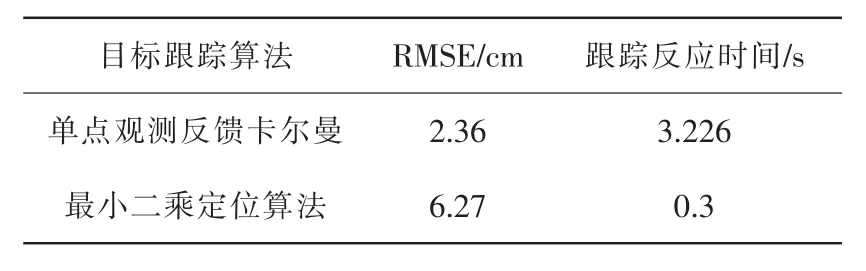
表1 兩種傳統定位算法的性能比較Tab.1 Performance comparison of two traditional location algorithms

采用卡爾曼濾波定位算法時，當目標發生突變運動時，目標狀態一般也發生較大的變化。此時卡爾曼的單步預測狀態估計與真實狀態誤差很大，但是由觀測值體現出來的系統狀態誤差卻較小。因此，以觀測值為基準，通過增強新加入信息的修正作用，以此加大濾波增益K，達到加快濾波跟蹤速度、減小估計誤差的目的。

以單個目標為例：卡爾曼增益Kk與狀態估計誤差協方差矩陣Pk+1/k和觀測噪聲協方差矩陣Rk有關。若系統采用相同結構和參數的傳感器節點，則Rk可視為常數。Kk隨Pk+1/k的增大而增大，且Pk+1/k體現了濾波的精度，Pk+1/k越小說明濾波越準確[13]。因此，Kk的增大是由濾波不準確，協方差矩陣較大所要求的。

其中：Kk為常規卡爾曼濾波在k時刻的增益；為附加增益。系統狀態估計方程重寫為

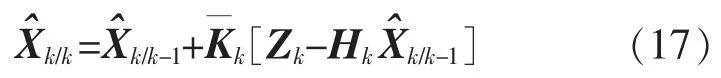
其余遞推公式保持不變。

式中：k0為系統狀態發生突變的時刻；Kz，k0為 k0時刻足以實現目標快速跟蹤的增益矩陣；λ為常數，一般取0.8～0.9。可通過設定一個非常大的協方差陣Pz，對式（8）、式（9）進行修正以確定 Kz，k0[13]。 協方差陣Pz代表濾波估值與狀態真值之間的誤差，但其并沒有一種標準的理論取法。

本文結合收斂速度快的最小二乘法來確定Kz，k0。在目標發生運動突變時，最小二乘法以其快速收斂的特性保證獲取較為準確的狀態估計，但其仍然存在較大的噪聲，因此先采用一階低通濾波器消除高頻噪聲：

假設利用最小二乘法經低通濾波器得到k0時刻的系統狀態估計為X?z，k0，則通過設計一個 Pz，k0：

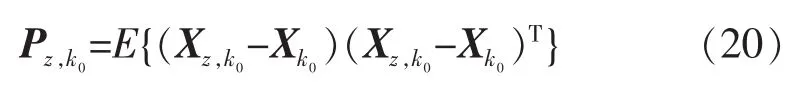
可得：

最終卡爾曼增益設計為

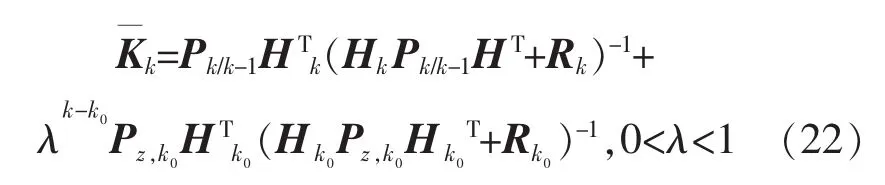
模型參數及初值的確定：

上述混合估計算法的模型參數及初值可按常規的卡爾曼濾波器來確定。若多目標跟蹤系統采用周期驅動異步測量策略且采樣周期為T，則過程噪聲協方差：

其中，λ為過程噪聲因子。

過程噪聲和量測噪聲必須滿足一定的數量級關系才能得到好的跟蹤效果。量測噪聲協方差的辨識原則為

P0可選擇范圍比較大，可設為單位陣I。系統初值X0則可通過最小二乘定位算法確定。

3 算法效果驗證

3.1 實驗平臺簡介

系統在邏輯結構上分為感知層、網絡通信層、應用層，實體垂直架構依次為分布式測量節點、基站、USB-ZigBee通信網關、數據服務中心。系統架構如圖3所示。

圖3 實驗平臺架構圖Fig.3 Configuration of experimental platform

12個分布式網絡超聲波測距節點均勻分布，在平面上組成一個大小為4 m×6 m，坐標從 （0，0）到（400，600）的有效監視區域。將監視區域劃分為6個網格，每個網格大小為2 m×2 m，包含4個節點；基站是在無線網絡覆蓋區中，負責整個網絡的資源分配和信息解析的單元；USB-ZigBee通信網關是負責基站和數據服務中心之間的信息傳遞，實現上下行雙向通信的單元；數據服務中心是采集無線傳感器網絡原始測量數據和利用數據融合定位算法計算目標位置信息的單元，并負責繪制目標軌跡曲線和存儲歷史數據；輪式移動機器人可在監測網絡內任意移動，作為系統的跟蹤目標。

3.2 速度突變情況的效果

針對移動目標速度突變運動的情況，將本文的混合估計算法嵌入到多目標跟蹤實驗平臺中，可得到如圖4的實驗結果。圖4（a）是目標以0.5 rad/s的速度運動到兩網格交界處并突然停止（速度變為0）的理想軌跡；圖 4（b）、（c）、（d）分別為最小二乘算法、常規卡爾曼濾波定位算法、混合估計算法的實際跟蹤軌跡圖。與收斂快速的最小二乘法相比，混合估計算法雖然收斂速度稍慢，但其對目標速度不發生大突變時的跟蹤更趨平滑準確；而與收斂速度慢的標準卡爾曼濾波相比，其對于目標速度不會突變時的跟蹤效果相當，但是對于移動目標速度突變時的收斂速度則快得多，跟蹤效果更佳。

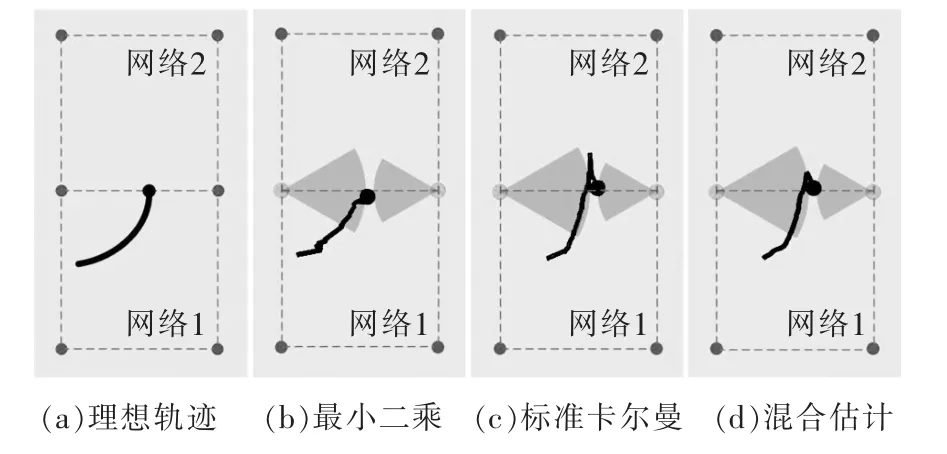
圖4 速度突變情況下性能對比Fig.4 Performance comparison of mutation rate case

3.3 實際跟蹤結果分析

圖5是兩臺輪式移動機器人同相位協同控制的實際效果圖。其中一臺機器人在左上方的網格內圍繞網格中心做半徑為0.5 m的圓周運動，線速度為0.3 m/s，角速度為0.6 rad/s，角速度變化在10%以內；另一臺機器人則在最下面四個網格圍繞中心節點做半徑為1 m，通過無線網絡反饋位置信息給機器人調節控制器輸出，使得其角速度和軸向角跟前一臺機器人一致的圓周運動，實現雙機器人的同相位協同控制。

圖5 雙機器人協同控制效果圖Fig.5 Diagram of dual-robot cooperative control

實驗結果表明，混合估計算法合理地融合了兩種定位算法的優點，不僅能準確跟蹤正常運動的目標而不丟失，且對于移動機器人在網格切換時速度和觀測模型發生突變時的運動也能達到平滑、快速跟蹤的效果。

4 結語

本文討論了無線傳感器網絡多目標跟蹤應用中目標運動特性多樣化的復雜情況及由其導致的跟蹤困難問題，并針對該問題提出了混合估計算法。該算法是一個自適應的校正過程，當目標移動速度不突變時，其能夠以常規的卡爾曼濾波定位算法出現，達到平滑且準確的目標跟蹤性能；而當目標運動速度發生突變時，其又能夠結合收斂速度快的最小二乘法來校正卡爾曼濾波增益，達到快速跟蹤的目的。通過搭建一個基于卡爾曼濾波的無線傳感器網絡多目標實時跟蹤實驗平臺，進行相關算法的效能驗證。實驗結果表明，本文的自適應混合估計算法具有良好的跟蹤性能。

[1] 杜曉通.無線傳感器網絡技術與工程應用[M].北京：機械出版社，2010.

[2]Yong D，Chen W，Li X.Using mobile beacons to locate sensors in obstructed environments[J].Journal of Parallel and Distributed Computing，2010，70（6）：644-656.

[3]Zhang R B，Zhang L L，Feng Y B.Very low energy consumption wireless sensor localization for danger environments with single mobile anchor node[J].Wireless Personal Communications，2008，47（4）：497-521.

[4] Kuang XH，Shao HH，Feng R.A new distributed localization scheme for wireless sensor networks[J].Acta Automatica Sinica，2008，34（3）：344-348.

[5]Mirela M，Mihaela C.Improved sensor network lifetime with multiple mobile sinks[J].Pervasive and Mobile Computing，2009，5（5）：542-555.

[6] 鄭巍，劉三陽，寇曉麗.動態傳感器網絡移動代理路由算法[J].控制與決策，2010，25（7）：1035-1039.

[7] Wang G J，Wang T，Jia W J.Adaptive location updates for mobile sinks in wireless sensor networks[J].Journal of Supercomputing，2009，47（2）：127-145.

[8]Camp T，Bolenq J，Davies V.A survey of mobility models for ad hoc network research[J].Wireless Communications and Mobile Computing，2002，2（5）：483-502.

[9] Kuo-Feng Ssu，Chia-Ho Ou，Jiau HC.Localization with mobile anchor points in wireless sensor networks[J].IEEE Transactions on Vehicular Technology，2005，54（3）：1187-1197.

[10]Yang Liu.Sun Zhen-dong.EKF-based adaptive sensor scheduling for target tracking[C]//IEEE International Symposium on Information Science and Engieering，2008：171-174.

[11]Rajendran V，Obraczka K，Garcia-Luna-Aceves JJ.Energy-efficient，collision-free medium access control for wireless sensor networks[C]//Proceeding of SenSys03，2003：181-192.

[12]Ye Jingzhi，Zhao Ling，Luo Wenfeng.Performances of localization algorithms in a prototype WSN system[J].Advanced Materials Research，2012（457-458）：723-727.

[13]孫楓，劉希斌.一個快速跟蹤的卡爾曼濾波算法及其在艦船組合導航中的應用[J].中國慣性技術學報，2000，8（4）：19-23.