軟夾芯夾層梁最大彎曲正應力的計算
郝景新,劉文金,吳新鳳(.中南林業科技大學,長沙40004;2.湖南省家具家飾工業設計中心,長沙40004)
軟夾芯夾層梁最大彎曲正應力的計算
郝景新1,2,劉文金1,2,吳新鳳1
(1.中南林業科技大學,長沙410004;2.湖南省家具家飾工業設計中心,長沙410004)
最大彎曲正應力是衡量夾層梁彎曲性能的重要參數之一,本文推導出了將軟夾芯夾層梁等效成等截面均質單層梁計算最大彎曲正應力的方法,并在此基礎上進行三點彎曲試驗的算例研究。結果表明:修正單層梁理論與層合梁理論計算的結果是一致的。當破壞載荷與夾層梁橫截面的尺寸一定時,隨著芯層與總厚度比的增加,修正單層梁理論計算的最大正應力值逐漸增加,而單層梁理論計算的結果為一恒定值。最大彎曲正應力修正公式的建立為夾層梁的工程應用提供理論基礎。
夾層梁;彎曲正應力;單層梁理論;彎曲特性
1 前言
如今,各種材料組合的復合層壓板廣泛應用于航天、軍事及民用領域,其優異的力學性能得到了眾多行業的認可。蜂窩夾層板是由上下各一層厚度較薄、剛度較大的材料與剛度較小的蜂窩芯層膠合而成的三層結構的復合層壓板,蜂窩芯可以是紙蜂窩、鋁蜂窩等金屬蜂窩,其中,基于紙蜂窩芯的木質夾層板由于其優異的比強度、比剛度性能廣泛應用于包裝行業、家具制造等民用領域[1~4]。
當夾心結構梁(板)承受彎曲載荷時,上面板承受壓應力,下面板承受拉應力,芯子主要承受剪切力,這種結構與工字梁相似,面板相當于工字梁的翼緣,芯板相當于工字梁的腹板,隨面板之間夾層厚度的增加,整個剖面的慣性矩呈冪級數增大[5,6]。最大彎曲正應力是衡量夾層梁(板)彎曲性能的重要參數之一,許多學者經常用傳統單層梁理論計算最大彎曲正應力[4,7,8]。由于夾層梁是由不同材料組成,每一層材料的彈性模量有時差異較大,用單層梁理論計算的最大正應力值往往誤差很大。因此筆者推導了夾層梁等效彈性模量的表達式,并在此基礎上修正了傳統單層梁理論計算最大彎曲正應力的公式,最后將不同的計算方法進行對比分析。
2 理論推導
2.1 單層梁橫截面最大彎曲正應力

式(1)中,σb為橫截面最大彎曲正應力;Pmax為破壞載荷;L為兩支座間的距離;b為夾層梁的寬度;h為夾層梁的厚度。
2.2 夾層梁的等效彈性模量
為了計算夾層梁橫截面最大彎曲正應力,首先將夾層梁等效成同截面尺寸的均質單層梁,推導出夾層梁的等效抗彎剛度和等效彈性模量,然后根據材料力學的理論計算而得。圖1為受力分析示意圖。
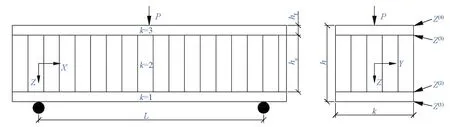
圖1 三點彎曲試驗的受力分析示意圖Fig.1 Three-point bending test of sandwich beam
如圖1所示,根據經典層合梁理論[5],蜂窩夾層梁的抗彎剛度可表示為:
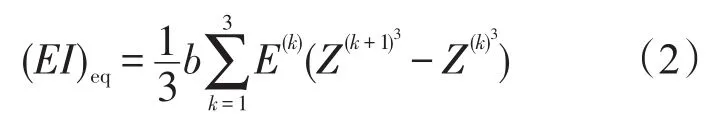
式(2)中,(EI)eq為等效抗彎剛度;E(k)為第k層的彈性模量;Z(k+1)為(k+1)層的Z軸坐標;Z(k)為k層的Z軸坐標。
由于芯層蜂窩彈性模量很小,中間層可忽略不計,并且上下表板對稱設置,則式(2)可簡化為:
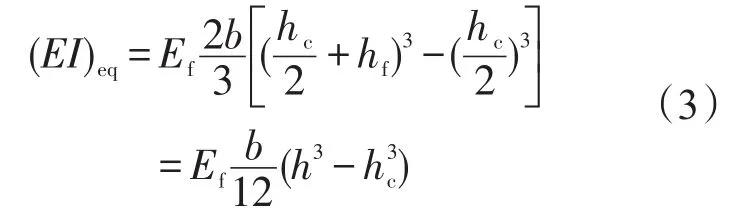
式(3)中,Ef=E(1)=E(3);Ef為表板彈性模量;hf為表板厚度;hc為芯層厚度。
如果將夾層梁等效成相同截面尺寸的均質單層梁,則等效截面慣性矩Ieq可表示為:

將式(4)代入式(3)中,推出:

式(5)中,Eeq指夾層梁等效彈性模量。
整理式(5),推出:

下面來分析不同的夾心結構對k值的影響。由圖2可知,隨著芯層與總厚度比的增加,k值逐漸減小。當這種比值等于0.3時,k等于0.97,這說明當芯層與總厚度的比小于0.3時,可以將表板的彈性模量近似成夾層梁的等效彈性模量。
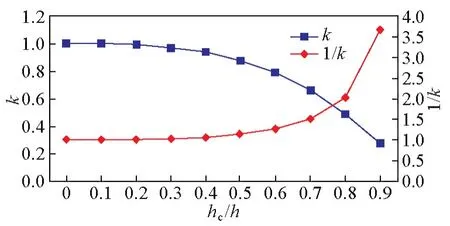
圖2 不同的夾層結構對k值的影響Fig.2 The effect of sandwich construction on value ofk
2.3 夾層梁橫截面最大正應力
根據材料力學中的公式[9,10],并將夾層梁的抗彎剛度進行置換,可推出:
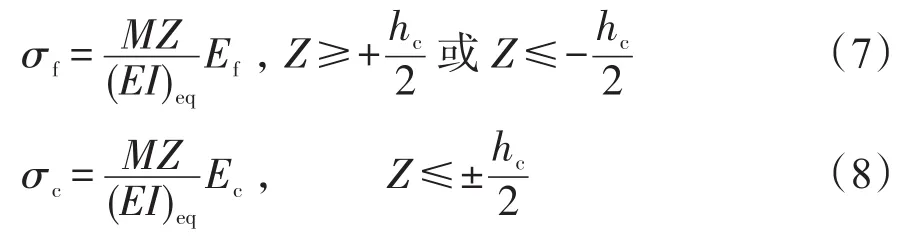
式中,σf指表板正應力;M指橫截面彎矩;Z為Z軸坐標值;σc指芯層蜂窩正應力;Ec指芯層蜂窩彈性模量。
對于紙蜂窩而言,忽略其面內剛度,即Ec≈0,我們推出σc≈0。橫截面正應力分布見圖3,即芯層中正應力可忽略不計,正應力從芯層與表板的接觸面開始向表板方向線性增加,上表板承受壓應力,下表板承受拉應力,應力最大值出現在上下表板的外表面上。
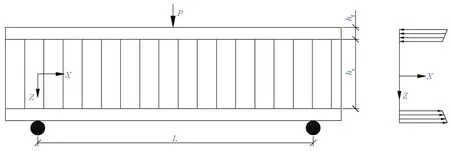
圖3 夾層梁橫截面正應力分布Fig.3 The distribution of normal stress along cross-sectional of sandwich beam
將式(6)代入式(7)中,推出:
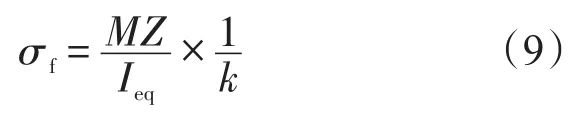
進行夾層梁三點彎曲試驗時,加載點處的彎矩可表示為:

式(10)中,P為橫向載荷。
將式(10)與式(4)代入式(9)中,推出:
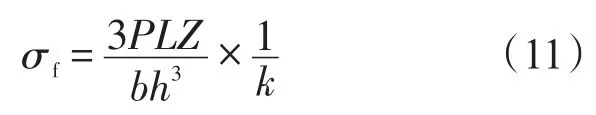

發現式(12)與式(1)形式基本相同,二者之間僅相差一個系數,而該系數與夾層結構的關系見圖2。當芯層厚度與總厚度比小于0.3時,系數的值界于1.0~1.03,這說明兩種方法計算的最大彎曲正應力可近似一樣。但當芯層厚度與總厚度的比大于0.3時,兩種方法計算的最大彎曲正應力具有明顯的差異。
3 算例
設Pmax=200 N,L=350 mm,b=60 mm,h= 20 mm或40 mm,Ec≈0。
為了驗證修正單層梁理論的有效性,本文引用基于層合梁理論計算最大彎曲正應力的公式作為對比[10]:
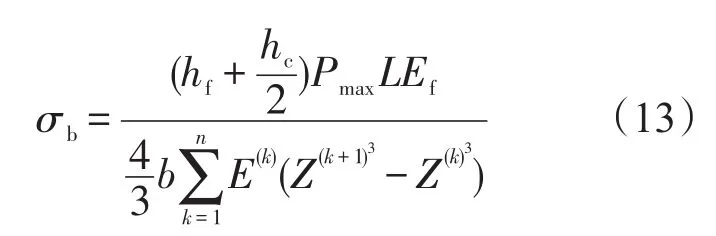
由圖4、圖5可知,模擬三點彎曲試驗時,修正單層梁理論與層合梁理論計算的結果是一致的,這說明修正單層梁理論預測夾層梁最大彎曲正應力是有效的。當破壞載荷與夾層梁橫截面的尺寸一定時,基于單層梁理論計算的最大正應力值是固定的,它與芯層厚度之間并沒有直接關系。而隨著夾層梁芯層與總厚度比的增加,修正單層梁理論計算的最大正應力值逐漸增加。當夾層梁芯層與總厚度比小于0.3時,修正單層梁理論與單層梁理論計算的最大正應力差異值小于3%,也就是說該種結構的夾層梁可直接等效成同截面的均質梁;而當芯層與總厚度比為0.9時,這種差異值增加到3.69倍。
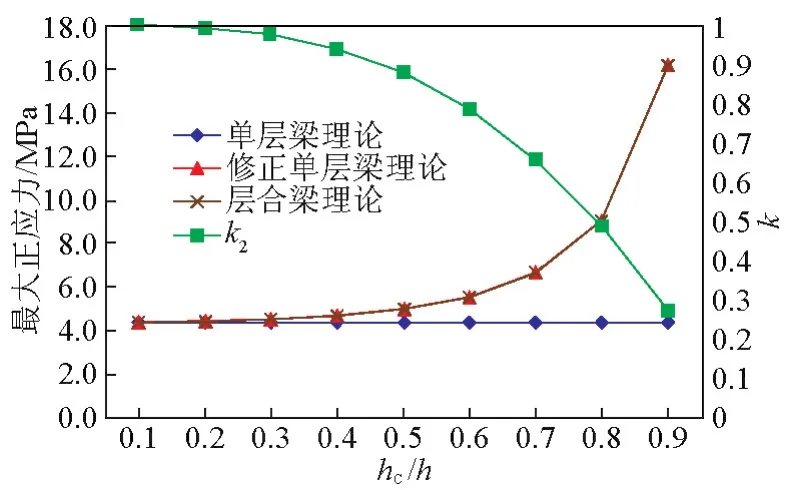
圖4 夾層梁橫截面最大正應力(h=20 mm)Fig.4 The maximum normal stress of sandwich beam(h=20 mm)
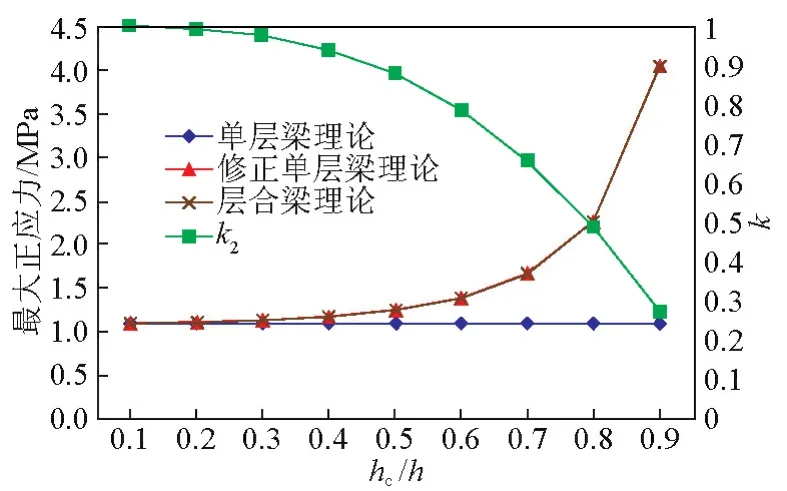
圖5 夾層梁橫截面最大正應力(h=40 mm)Fig.5 The maximum normal stress of sandwich beam(h=40 mm)
4 結語
本文建立了將軟夾芯夾層梁等效成等截面均質單層梁計算最大彎曲正應力的方法,并在此基礎上進行算例研究,結果表明:模擬三點彎曲試驗時,修正單層梁理論與層合梁理論計算的結果是一致的。當破壞載荷與夾層梁橫截面的尺寸一定時,隨著芯層與總厚度比的增加,修正單層梁理論計算的最大正應力值逐漸增加而單層梁理論計算的結果為一恒定值。
[1]郝景新,劉文金,吳新鳳.基于紙質蜂窩的家具板件結構與工藝技術[J].包裝工程,2012,33(22):29-32.
[2]郝景新,劉文金,吳新鳳.V形槽折疊式空心木質腿的結構與工藝[J].林產工業,2012,39(6):38-40.
[3]郝景新,劉文金,吳新鳳.考慮剪切變形的蜂窩夾層木質復合梁的彎曲特性[J].木材加工機械,2013,24(4):29-33.
[4]徐朝陽,李大綱.木質蜂窩夾芯包裝材料抗彎性能研究[J].包裝工程,2007,28(8):16-18.
[5] Allen H G.Analysis and Design of Structural Sandwich Boards [M].Oxford:Pergamon Press,1969.
[6]Carlsson L A,Kardomateas G A.Structural and Failure Mechanics of Sandwich Composites[M].New York:Springer Science and Business Media B V,2011.
[7]徐朝陽.木質復合蜂窩夾芯材料性能研究[D].南京:南京林業大學,2007.
[8]司琳琳,唐忠榮,劉 林.新型輕質家具材料-木質材料強化蜂窩紙芯復合板的研制[J].林業機械與木工設備,2009,37(1):12-14.
[9]Hibbeler R C.材料力學(原書第六版)[M].武建華縮編.重慶:重慶大學出版社,2007.
[10]許小君,李大綱,周 敏.新型復合夾芯包裝材料的彎曲正應力分析[J].包裝工程,2003,24(5):128-130.
The calculation of maximum bending normal stress for sandwich beam based on revised single beam theory
Hao Jingxin,Liu Wenjin,Wu Xinfeng
(1.Central South University of Forestry and Technology,Changsha 410004,China;2.Hunan I.D.Center of Furniture and Furnishing,Changsha 410004,China)
Maximum bending normal stress is one of the important parameters to measure flexural property of sandwich beam.Therefore,new methodology to calculate the stress is proposed based on the equivalent single beam theory,after that the numerical examples are demonstrated according to three point flexure test.The results showed that revised single beam theory (RSBT)are equivalent to multi-layer theory(MLT).When cross section of beam and maximum loading are fixed,the maximum bending normal stress calculated by RSBT is increased accordingly with increasing ratio of core thickness to the whole,but the result is constant for single beam theory(SBT).RSBT is set up to provide a new method for sandwich construction application in engineering industry.
sandwich beam;bending normal stress;single beam theory;bending property
TS62
A
1009-1742(2014)04-0092-04
2013-12-19
湖南省教育廳優秀青年(13B151);省研究生創新基金(CX2012B315)
郝景新,1982年出生,山東濟寧市人,工程師,研究方向為家具設計與工程;E-mail:haojingxin1@163.com

