基于階比分析和EEMD的軸承故障診斷

呂建新，黃炯龍，曹紅燕，陳文龍

(1.武警工程大學，陜西西安 710086;2.廣西師范大學電子工程學院，廣西桂林 541004)

基于階比分析和EEMD的軸承故障診斷

呂建新1，黃炯龍1，曹紅燕2，陳文龍1

(1.武警工程大學，陜西西安 710086;2.廣西師范大學電子工程學院，廣西桂林 541004)

針對軸承故障診斷中軸的轉速變化影響振動信號提取的特點，將階比分析法與總體平均經驗模式分解方法相結合，提出一種研究軸承非平穩振動信號的故障診斷方法。對軸承的振動信號按傳統的方法在時域上進行采樣，通過計算階比跟蹤將其轉化為角域上的準平穩信號，對上述角域信號進行總體平均經驗模態分解得出包含故障信息的模態函數分量，并對該分量進行頻譜分析。應用結果表明:該方法能夠有效地提取出軸承的故障特征。

階比分析;總體平均經驗模式分解;軸承;故障診斷

滾動軸承是應用最為廣泛、最為重要的旋轉機械設備部件之一，一般都是長期運行的易損件。因此滾動軸承通常是機械設備中故障高發部件［1］。與此同時，滾動軸承作為機床的重要組成部件，也是機床容易發生故障的部位，其運行的好壞直接影響整臺設備的工作性能及使用壽命［2］。因此，對滾動軸承的運行狀態進行監測并及時發現其中存在的故障隱患在機床的使用具有十分重要的意義，這點對大型復雜機床尤甚。

在機床的運行過程中，轉速是時刻變化的，而且很多故障信息往往只有在加速的過程中才能表現出來。在上述情況下，常用信號處理方法是在進行故障診斷時效果往往不太好。旋轉運動作為機床的一種主要運動形式，在機床運行時，雖然這些加速過程中的振動信號主要頻率成分相差很大，但都與轉速有著密切的關系。利用階比跟蹤技術在角域分析這些信號即可消除時域分析時轉速對其出現周期的影響，進而精確定位到這些信號［3］。

希爾伯特黃變換［4］(Hilbert-Huang Transform，HHT)由美國航空航天局Dr.Huang于1998年提出，被認為是近年來對以傅立葉變換為基礎的線性和穩態譜分析的一個重大突破。文獻 ［5］將階比分析與EMD相結合，克服了傳統頻譜分析在變轉速軸承故障轉動中頻率模糊的難題，實現了滾動軸承故障的快速診斷。

然而EMD算法本身也存在一些不足，如均值與停止條件、端點效應、模式混淆等。為解決經典EMD方法模式混疊問題，Wu和Huang在對白噪聲進行EMD分解深入研究的基礎上［6］，提出了一種新的噪聲輔助數據分析方法，即總體平均經驗模式分解方法 (Ensemble Empirical Mode Decomposition，EEMD)，該方法將原始信號加入白噪聲進行整體的EMD分解，然后對分解結果進行平均值處理。

由此，本文作者提出一種將階比分析與EEMD相結合的軸承故障診斷方法。首先通過階比分析方法實現了軸承振動信號從時域向角域的轉變，然后對角域的振動數據進行EEMD分解，得到一系列高頻固有模態函數及相關參數，然后對包含有軸承故障信息的模態函數進行了頻譜分析。通過實例分析表明，該方法能夠在克服轉速波動的同時快速有效地提取出滾動軸承的故障信息。

1 階比分析

階比分析的第一步將時域的非穩態時變信號通過等角度采樣的方式轉變為角域準穩態信號，也稱之為階比跟蹤。因此，階比分析方法的關鍵在于實現階比跟蹤，從而將時變信號轉變為角域準平穩信號。傳統的階比跟蹤方法是直接通過模擬設備實現對模擬的振動信號進行恒定角增量采樣的，但所使用的跟蹤濾波器等硬件不但結構復雜、價格昂貴，而且在旋轉機械轉速變化快時，其跟蹤精度得不到保證，因而限制了其在工程實際中的廣泛應用［7］。

計算階比跟蹤與上述傳統的硬件階比跟蹤方法相比在各方面已大為簡化，在精度方面也得到了很明顯的提高，其實現思想是對振動信號和轉速信號單獨采樣，再通過相應的插值算法用軟件實現等角度間隔采樣，它最大的優點在于無需特定的硬件，克服了傳統階比跟蹤算法中成本較高的不足。

2 EEMD分解

EEMD作為一種自適應的處理方法，能夠對非平穩時變信號的瞬態特征進行有效的提取。EEMD在分解過程中充分利用白噪聲頻率均勻分布特性，通過在振動信號加入高斯白噪聲，使得該信號在不同尺度上表現出明顯的連續性，從而改變其極值點的特性，促進信號的抗混分解，有效地避免了EMD分解中的混疊現象。

EEMD的具體分解步驟如下［6］

(1)在輸入的信號x(t)上加入等長度正態分布的隨機高斯白噪聲序列ni(t)，得到加噪后的信號xi(t)

式中:xi(t)為第i次加噪后得到的信號，k為所加白噪聲信號的幅值系數。

(2)對經過上述加噪處理后的信號xi(t)按EMD分解步驟進行分解，從而得到固有模態分量cij(t)和余項ri(t)，其中cij(t)表示第i次加噪處理后再進行EMD分解所得的第j個分量。

(3)重復上述步驟，根據不相關的隨機序列統計均值為0原理，將上述各固有模態分量cij(t)進行整體平均計算，通過計算可以對多次加入白噪聲對真實IMF的影響進行抵消，最終再對每個IMF計算平均值:

式中:ci(t)作為EEMD分解后得到的第j個IMF，N為指添加白噪聲序列的數目。

3 基于階比分析和EEMD的故障提取

基于階比分析和EEMD的故障診斷具體步驟如下如下:

(1)為減小機床運行過程中噪聲對信號提取的影響，這里通過db4小波對振動信號進行閥值降噪;

(2)由于這里只用到在很短時間內的振動數據，根據文獻 ［8］，軸承所在的參考軸在短時間內可看作是一種勻變速運動，因此，轉角與時間的函數關系可以通過多項式表示出來

式中:bn為待定的系數;t為信號采樣對應的時間。

在采集到的時域振動信號中，轉過相等角度Δα的連續時間為ti，可得

將式(4)代入式 (3)中，可求得待定系數bn。為簡化計算過程這里取n=3時進行計算。

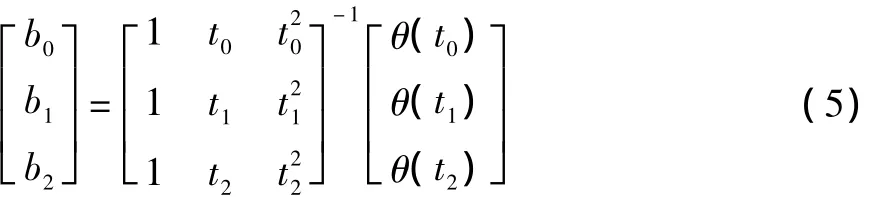
求出bi(i=1，2，3)，再代入式 (3)即求出等角度重采樣所對應的時間點ti(i=1，2，3)

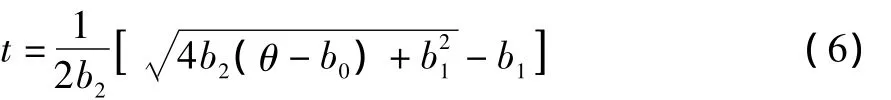
將ti(i=1，2，3)和對之相應的參考軸轉角代入式(5)可得

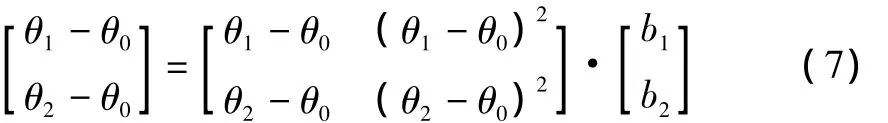
通過上述計算即可以得出關于等角度采樣點的方程，在求出等角度重采樣振動信號對應的時間點后，通過三次樣條插值算法即可實現時域信號的計算階比跟蹤重采樣，從而得到等角度分布的采樣點χ(m)。

(3)對經過階比跟蹤處理后的角域準平穩信號χ(m)進行上述EEMD分解，得到其各個IMF分量，c1，c2，…，cn。

(4)對上述各IMF的瞬時幅值進行頻譜分析，即可有效地實現對故障軸承相關故障信息的提取。

4 實例與分析

某型數控機床的主軸軸承出現故障。通過安裝在軸承座上的振動傳感器獲取機床運轉時的振動信號，與此同時通過轉速傳感器獲取該機床主軸的實時轉速數據，數據采樣頻率為10 kHz，采樣時間為10 s。使用基于LABVIEW平臺的軸承故障診斷軟件對采集的信號進行分析。

圖1和圖2是是采集到的的原始時域振動信號和轉速信號。可以看出該軸承的故障信息在振動時域圖中并不明顯。從圖2中可以看出，整個采集過程中該機床主軸的轉速是時刻變化的，若直接對時域振動數據進行FFT變化，將會導致頻率模糊。因此，采用階比跟蹤法對時域信號進行角域重采樣以克服轉速的變化對故障信息提取的不良影響。

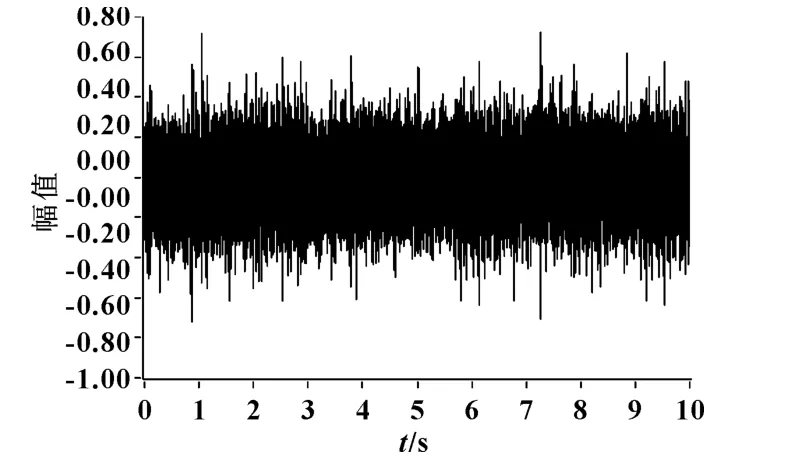
圖1 時域振動信號

圖2 轉速信號

對角域重采樣后的信號再進行EEMD分解，得到11個IMF與一個余量。由于故障信息都包含在IMF中，這里以第一個IMF為例進行頻譜分析。圖3為分析結果。從圖中可以明顯的看出故障階次order= 10，經查詢該故障階次對應的是該類型軸承的內圈疲勞裂紋。在對該故障軸承進行分解后，證實該診斷結果的正確性。

圖3 角域信號EEMD分解

為了對比EEMD和EMD在階比重采樣信號的結果，用EMD分解同一角域重采樣信號，結果如圖4所示，雖然經過EMD分解的重采樣信號也能判斷出特征階次，但受到如均值與停止條件、端點效應、模式混淆等問題的影響，故障診斷的效果不如EEMD明顯，而且在運算速度方面EEMD的分解速度較快。

圖4 角域信號EMD分解

5 結束語

(1)針對變轉速工況影響時機床主軸軸承的振動信號的分析，提出了一種采用階比分析和EEMD分解相結合的滾動軸承故障診斷的方法。

(2)采用小波消噪和角域重采樣能有效地將強噪聲條件下的非平穩時變信號轉換為角域準平穩信號，避免了傳統頻譜分析中頻率模糊的問題。

(3)對EEMD分解后的角域重采樣信號的高頻部分進行分析，有效避免了低頻嚙合信號的影響，與EMD方法相比，在診斷效果和計算時間方面都有所提高。某型機床主軸軸承的實例證實文中方法提取的軸承故障信號明顯，具有良好的識別效果。

(4)該方法不需要經過其他復雜的模式識方法既可直接從圖譜中讀出故障信息，為軸承狀態的在線檢測和故障診斷提供了新的思路。

［1］周云龍，宋延宏，陳軍，等.基于HHT與GA-BP網絡的軸承故障診斷方法研究［J］.機床與液壓，2010，38 (17):133－137.

［2］蔣宇，李志雄，唐茗，等.EMD下軸承故障程度診斷技術的研究［J］.機床與液壓，2009，37(8):257－260.

［3］程利軍，張英堂，李志寧，等.基于階比跟蹤及共振解調的連桿軸承故障診斷研究［J］.內燃機工程，2012，33 (5):67－73.

［4］WU Zhaohua，HUANG N E.A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method［J］.Proc R Soc Lond A，2004，460:1597－1611.

［5］康海英，欒軍英，鄭海起，等.基于階次跟蹤和經驗模態分解的滾動軸承包絡解調分析［J］.機械工程學報，2007，43(8):119－122.

［6］WU Zhaohua，HUANG N E.Ensemble Empirical Mode Decomposition:a Noise Assisted Data Analysis Method［J］.Advances in Adaptive Data Analysis，2009，1(1):1－4.

［7］趙曉平，張令彌，郭勤濤.旋轉機械階比跟蹤技術研究進展綜述［J］.地震工程與工程振動，2008，28(6):213－219.

［8］MUNCKEDS F K R.Analysis of Computed Order Tracking［J］.Mechanical Systems and Signal Processing，1997，11 (2):187－205.

Bearing Fault Diagnosis Based on Order Tracking Analysis and EEMD

LV Jianxin1，HUANG Jionlong1，CAO Hongyan2，CHEN Wenlong1
(1.Engineering University of CAPF，Xi'an Shaanxi 710086，China; 2.College of Electronic Engineering，Guangxi Normal University，Guilin Guangxi 541004，China)

Aimed at the characteristics of fault vibration signals processes were affected by the variable speed of the bearing in fault diagnosis，a new fault diagnosis method combined of order tracking analysis with Ensemble Empirical Mode Decomposition(EEMD)was proposed for studying of signals of unstable vibration of bearing.The bearing vibration signal was sampled at constant time increments traditionally，and computer order tracking was used to transform the data at constant angle increments in angle-domain.With the method of EEMD，the angle domain stationary signal was adaptively decomposed into a finite number of Intrinsic Mode Function(IMF)containing fault information.Each IMF was analyzed by frequency spectrum.The application results show that this method can effectively extract the fault characteristics of the bearing.

Order tracking analysis;EEMD;Bearing;Fault diagnosis

H115

A

1001－3881(2014)9－170－3

10.3969/j.issn.1001－3881.2014.09.047

2013－04－15

呂建新 (1967—)，男，教授，碩士學位，碩士生導師，主要從事工程機械故障診斷研究。E－mail:gphjl @sina.com。