基于遺傳算法的無刷直流電動機自適應模糊控制

侯春杰，張 雷，孟令瑞

(河南科技大學，洛陽471023)

0 引 言

由于無刷直流電動機(以下簡稱BLDCM)具有功率密度高、體積小、調速性能好且結構簡單的特點，它在汽車、工具、工業工控、航天等領域應用廣泛［1-3］。

目前采用遺傳算法(以下簡稱GA)優化模糊控制器的研究有很多［4-9］。文獻［7］采用了十進制的遺傳算法編碼方式，可以得到全局最佳規則庫，仿真結果較好。文獻［8］通過實數編碼的GA 對隸屬度函數的位置及寬度進行共同編碼，引入適當的隸屬度函數評判機制來生成最優的隸屬度函數，仿真結果表明優化后的模糊控制器控制品質有較大的改善和提高。文獻［9］提出了二維調整因子的概念，利用GA 優化選取二維調整因子、量化因子以及比例因子，減小了搜索空間。

本文利用GA 同時優化控制規則和隸屬度函數，并在MATLAB/Simulink 中搭建仿真模型，將遺傳算法與自適應模糊控制相結合［10-11］。仿真表明，基于該方法的BLDCM 自適應模糊控制系統，響應快、無超調、穩態誤差小，并且具有較強的自適應性和魯棒性。

1 無刷直流電動機雙閉環控制系統

1.1 BLDCM 的數學模型

本文數學模型采用兩相導通星形三相六狀態，并滿足以下假定:

1)轉子磁阻不隨位置變化而變化，三相繞組完全對稱;

2)不計電樞反應、換相過程和齒槽的影響;

3)在定子內表面，電樞導體呈均勻連續分布;

4)磁路不飽和，忽略磁滯損耗以及渦流損耗。

基于以上假設，三相對稱BLDCM 的相電壓方程:

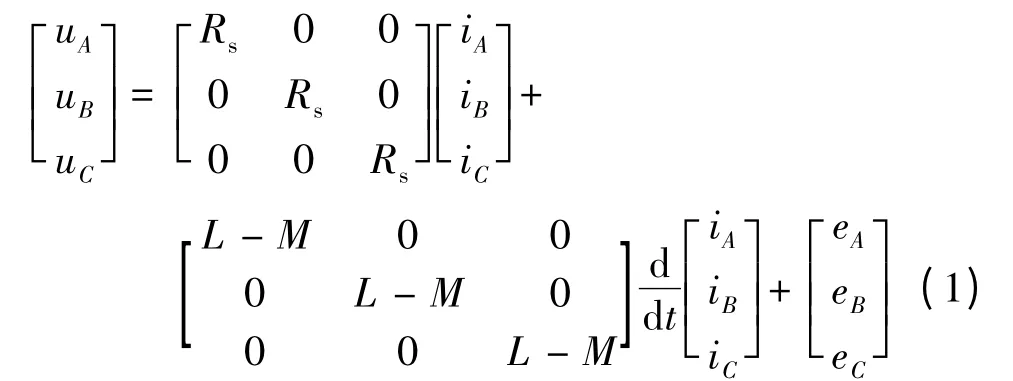
式中:eA，eB，eC為反電動勢;iA，iB，iC為三相定子繞組的相電流;uA，uB，uC為三相定子繞組的相電壓;Rs為繞組電阻;L 為自感;M 為互感。

電磁轉矩的方程:

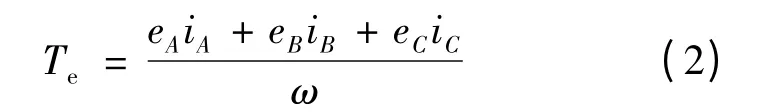
轉子運動方程:

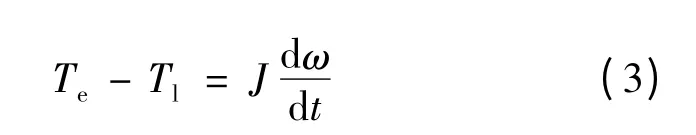
式中:Te為電磁轉矩;ω 為轉子機械角加速度;Tl為負載轉矩;J 為轉子的轉動慣量。

1.2 雙閉環控制系統

速度環采用Fuzzy 控制器為外環，并使用GA 對其進行優化，優化后的Fuzzy 控制器輸入為給定轉速n*與實際速度回饋值n 的差值，輸出為內環的給定值。內環為PI 調節器組成的電流環，外環輸出的給定電流值i*減去采樣值i 作為PI 調節器的輸入，輸出為BLDCM 的給定電壓。采用這種雙閉環控制策略，能恰當地發揮速度負反饋和電流負反饋的作用，使控制系統具有良好的動、靜態特性。圖1 為BLDCM 雙閉環控制系統的結構圖。

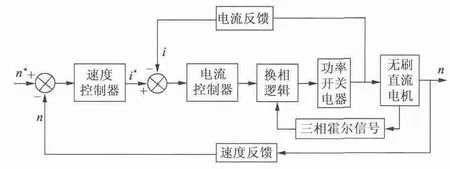
圖1 BLDCM 雙閉環控制系統的結構圖

2 GA 優化自適應模糊控制

2.1 個體編碼

對于隸屬度函數的形狀，本文選擇三角形隸屬度函數，采用十進制編碼方式。其可由3 個變量確定:左右端點的橫坐標以及頂點橫坐標。如圖2 所示，選取三點橫坐標作為優化參數，即對{x1，x2，x3，x4，x5}進行編碼。對于兩輸入三輸出的系統而言，其隸屬度函數的編碼為5 ×5 =25 的編碼串。

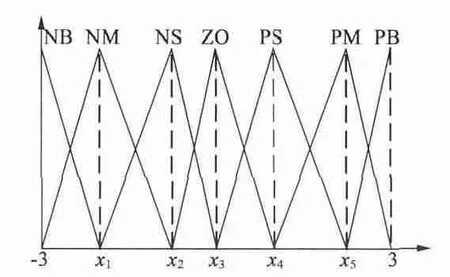
圖2 模糊變量的隸屬度函數圖形

對于控制規則的編碼，約定1 代表NB，2 代表NM，3 代表NS，4 代表ZO，5 代表PS，6 代表PM，7代表PB，模糊規則可拉伸成147 位的數字編碼串。

將隸屬度函數和控制規則的編碼聯合起來，就得到長度為25 +147 =172 位的染色體編碼串。

2.2 適應度函數

本文目標函數采用誤差絕對值時間積分性能指標，加上系統輸出的二次方項以免控制量太大，加入懲罰函數防止超調，如果超調，就將超調量加入最佳指標式子中。

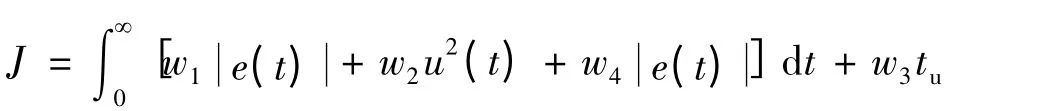
式中:u(t)為控制器輸出;e(t)為系統誤差;w1，w2，w3，w4為權值，且w4?w1，tu為上升時間。

因種群收斂可能出現除零，所以將適應度函數設為fit=1/(1 +J)。

2.3 選擇操作

2.4 交叉算子

編碼串的前25 位是隸屬度函數的編碼，后147位為規則編碼。假若按照一般的交叉方法，容易產生一些病態或者不合理的后代。因此本文采用分步一致交叉方法。對于前25 位隸屬度函數的編碼，因有5 個變量，所以分成5 組，每組5 位編碼，組與組之間進行交叉互換。對于后147 位規則的編碼，首先將等位基因比較，若其差值絕對值小于或者等于1，則等位基因可以互換，因此可防止控制作用發生突變及其引起的控制系統的劇烈震蕩。

2.5 變異算子

分步進行隸屬度函數和規則的變異操作。對于前25 位編碼，若變異的概率小于0.01，并且變異位加上1 仍小于后面的的數時，實施變異。針對后147 位編碼，如果變異概率小于給定變值，則變異位基因值+1 或-1。變異后的數字小于1 時令該基因值等于1，大于7 時令該基因值等于7。為防止產生不合理規則，變異量只能是+1 或者-1。

表1 至表3 為GA 優化后的控制規則。

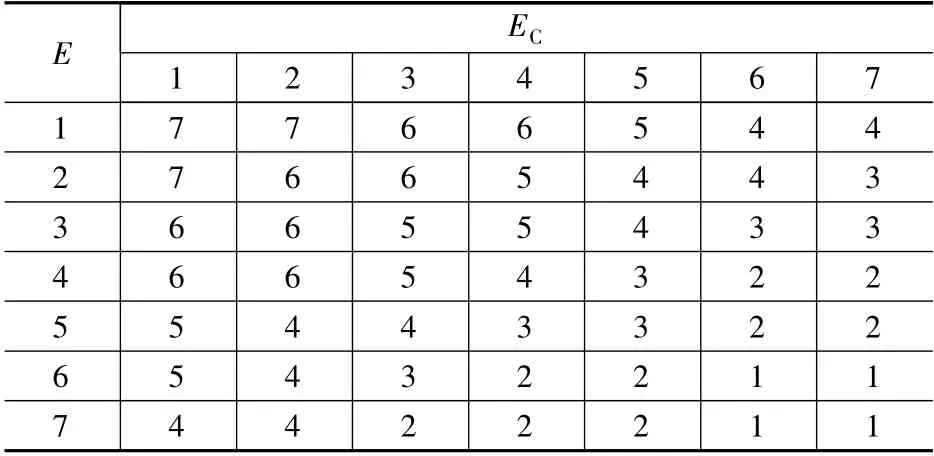
表1 Δkp 優化規則表

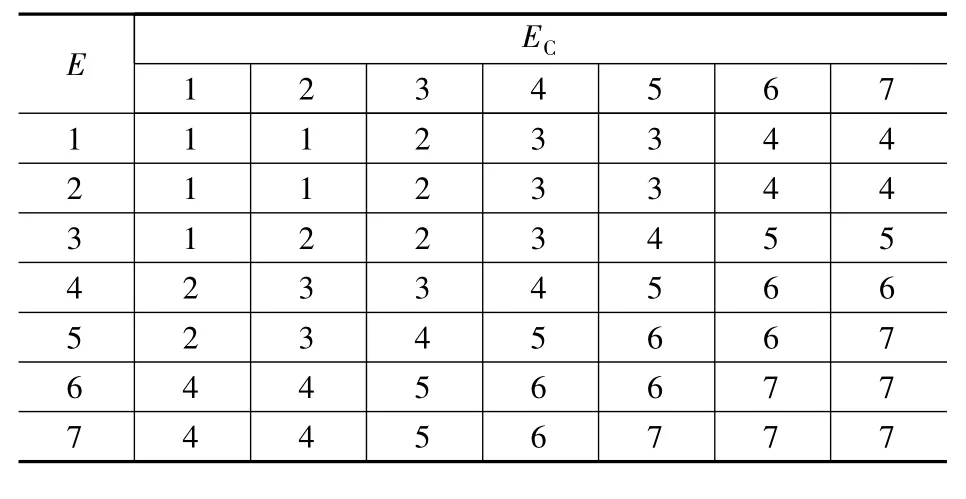
表2 Δki 優化規則表

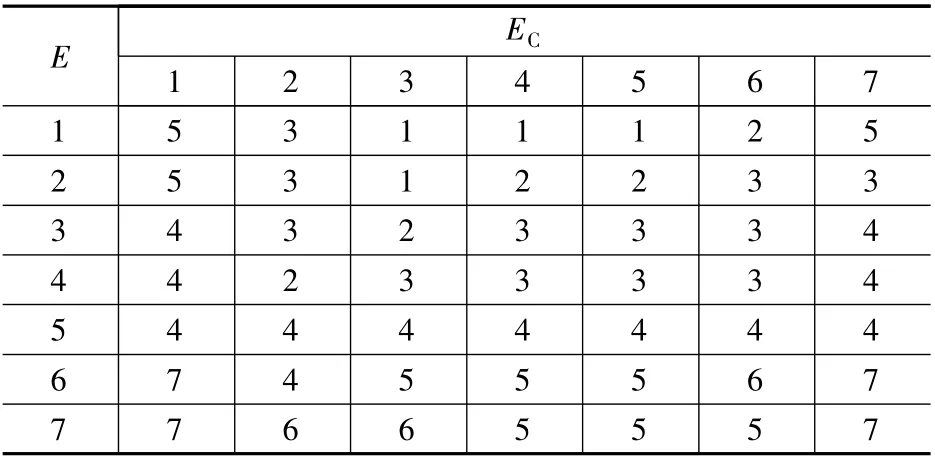
表3 Δkd 優化規則表

2.6 基于GA 優化的自適應模糊控制系統

遺傳算法優化參數，自動生成最優的隸屬度函數和控制規則，通過程序寫入模糊控制器。圖3 為基于GA 優化的自適應模糊控制器的仿真模型。

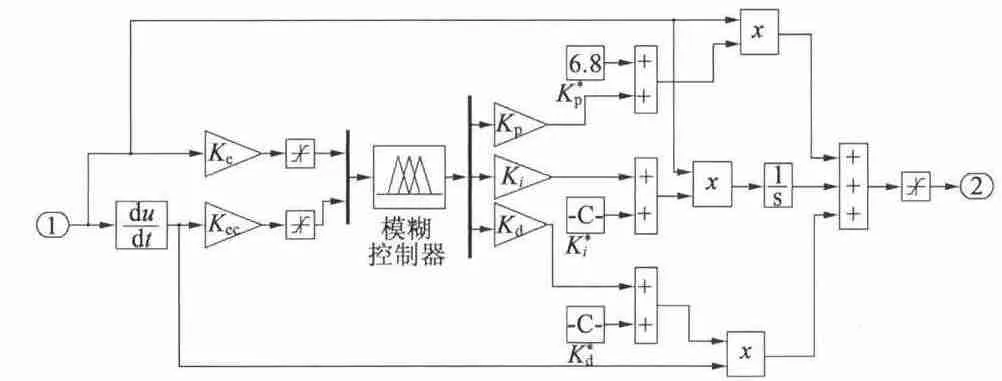
圖3 模糊自適應PID 控制模塊仿真圖

3 仿真結果及分析

GA 參數:種群大小等于30，進化代數選取100。變異概率pm=0. 01，交叉概率pc=0. 7。w1=0.999，w2=0.001，w3=2，w4=100。

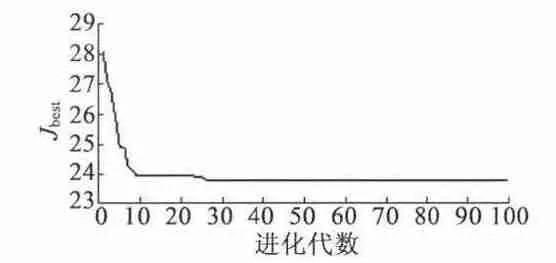
圖4 目標函數J 的優化過程

圖4 為目標函數的優化過程。隨著進化過程的進行，目標函數逐漸減小，當種群進化到第26 代時，目標函數達到最優解。

圖5 為采用GA 優化后的控制器階躍響應圖，由圖5 可知，采用該控制器的控制系統沒有超調，響應迅速并能較快恢復穩定。

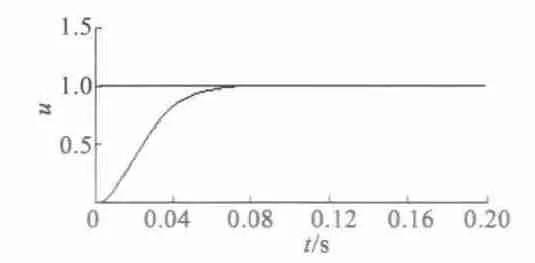
圖5 GA 優化后模糊PID 控制的階躍響應曲線

經遺傳算法優化后的隸屬度函數及模糊規則用于Fuzzy 控制器，選取Mamaddni 作為模糊化方法，反模糊化使用面積中心法，將控制器用于MATLAB雙閉環控制系統中進行仿真。

電機參數:額定電壓U =12 V，極對數p =4，定子電阻R=0.65 Ω，有效電感L =0.24 ×10-3H，轉動慣量J=2.1 ×10-5kg·m2，摩擦系數1 ×10-5，仿真時長0.2 s。

在變換轉速試驗中，系統無負載起動，起始n =600 r/min，t=0.1 s 時n =1 000r/min。電機轉速對比仿真曲線如下。

圖6 為轉速對比曲線，圖7 為轉速對比曲線的局部放大圖。仿真結果表明，基于GA 優化后的控制器，系統上升時間短，無超調，穩態誤差小。

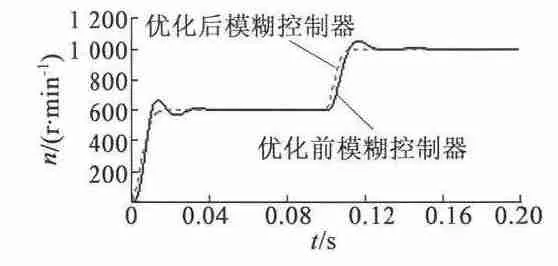
圖6 轉速對比波形

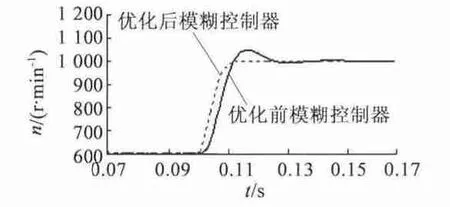
圖7 轉速響應對比曲線局部放大圖

改變負載試驗中，在0.15 s 時施加負載Tl=20×10-3N·m，得到轉速對比波形如圖8 所示，ia波形、ea波形和Te波形如圖9 所示。

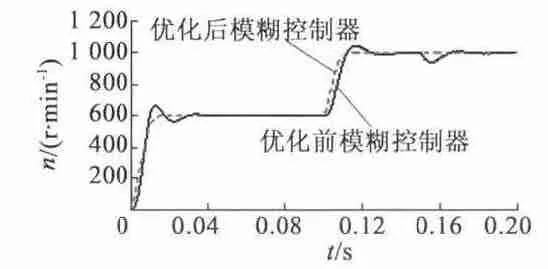
圖8 施加負載的轉速對比波形

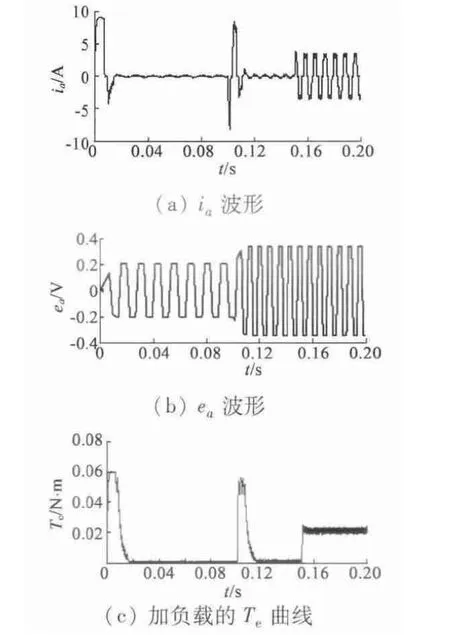
圖9 ia，ea，Te 波形

從圖8 可以看出，經遺傳算法優化后的控制器，在改變負載時擾動小，并很快又達到額定轉速，具有較好的系統抗干擾性和魯棒性。

從圖9(a)可以看出，在空載運行時，相電流很快到達穩定，0.15 s 施加負載后，為增大電磁轉矩，帶動外界負載，ia增大。圖9(b)顯示，系統空載時，ea為理想梯形波，其頂部約為120°，0.15 s 時改變Te，幅值略微變大。從圖9(c)可以看出，空載運行時，達到最大的起動轉矩，變換速度時引起轉矩脈動并迅速恢復穩定。0.15 s 時加入負載運行，轉矩迅速增大并保持穩定，整個過程中轉矩脈動較小。

4 結 語

本文提出基于遺傳優化機制的自適應模糊控制器設計方法，并用于BLDCM 的控制系統。這種設計方法能夠自動生成最優的隸屬度函數以及相應的模糊控制規則集合。MATLAB 仿真表明，采用遺傳算法優化自適應Fuzzy-PID 控制器的BLDCM 控制系統具有響應迅速、超調較小、無穩態誤差等優點。尤其在負載發生變化時，系統能很快再次穩定下來，具有較好的適應能力和魯棒性。

［1］ 蔣旭益，王立標.基于自適應模糊PID 無刷直流電機控制研究［J］.科學技術與工程，2011，11(27):6720 -6723.

［2］ 張小莉，張波.無刷直流電機自適應模糊控制系統建模與仿真［J］.機電一體化，2011，17(4):28 -32.

［3］ 孫佃升，白連平.模糊自適應PID 控制器在無刷直流電機控制系統中的應用［J］.電氣傳動，2009，39(10):63 -66.

［4］ 孫霞.基于遺傳優化的無刷直流電機模糊控制的研究［J］.煤礦機械，2011，32(10):104 -106.

［5］ 范冰潔，李玉忍，陳永祿.基于遺傳算法的無刷直流電機控制參數優化［J］.計算機仿真，2009，26(8):188 -192.

［6］ JAMALUDIN J，RAHIM N A，HEW W P.Development of a selftuning fuzzy logic controller for intelligent control of elevator systems［J］.Engineering Applications of Artificial Intelligence，2009，(22):1167 -1178.

［7］ 邵克勇，張鴻雁. 一種基于GA 的模糊控制規則優化新方法［J］.化工自動化及儀表，2011，38(3):261 -264.

［8］ 王鋒，張國煊，張懷相. 模糊隸屬度函數的遺傳優化［J］. 杭州電子科技大學學報，2009，29(4):34 -37.

［9］ 劉鎮，李程遠.用遺傳算法優化模糊控制規則［J］.貴州工業大學學報，2009，28(5):7 -11.

［10］ 楊璽.基于遺傳算法的模糊控制器規則優化［J］.電氣傳動自動化，2010，32(5):41 -44.

［11］ 董嬌玲.基于遺傳算法優化可調整控制規則的模糊控制［J］.計算機應用與軟件，2010，27(11):203 -205.