基于C環境下的Schim idt正交化方法實現
董曉萌,李 樂
(渭南師范學院 數學與信息科學學院,陜西 渭南714000)
用正交基的好處在于數值計算上,不用正交基計算不穩定,會隨著計算過程逐步積累誤差,可能會使得誤差過大計算結果根本不可用,而正交基不會發生這種問題。由于標準正交基在歐氏空間中占有特殊的地位,所以有必要來討論正交化過程。化便可得到V的一組標準正交基要得到這個結果很麻煩,如果有很多個向量計算量相當大,所以想得到一組單位正交的向量組花費時間多,計算容易出錯,所以編寫了正交化過程的C程序,該程序對矩陣進一步進行Schimidt正交化節省了時間,減少了工作量,且提高了效率。
1 Schim idt正交化原理
把一組線性無關的向量變成一單位正交向量組的方法稱為 Schimidt(施密特)正交化過程[1]。
歐氏空間V中任一組線性無關的元素α1,α2,…,αs都可以通過施密特正交化過程化為兩兩正交的元素 β1,β2,…,βs,且 α1,α2,…,αs與 β1,β2,…,βs等價,施密特正交化過程如下[2]:
令 β1=α1

βs=進而單位
2 向量正交化的C語言實現
C語言實現如下[3]。

printf("請輸入需正交化的向量組個數相當于矩陣的行數: ");
scanf("%d",&n);


3 實例分析
例:把 α1=(0,1,-1,1,1)α2=(-1,2,-1,1,2),α3=(-1,1,1,0,-1),α4=(-1,1,0,1,2),α5=(1,2,0,0,3),α6=(-2,1,0,0,0),α7=(-1,0,1,2,0),α8=(0,-1,2,1,1),α9=(2,-1,1,-1,-1),α10=(2,2,-1,-1,1)化為標準正交向量組[4]。
在 C 程序中,輸入向量 α1,α2,α3,α4,α5,α6,α7,α8,α9,α10原始數據值,再運行相關程序,就可直接得到施密特Schimidt正交化的向量 γ1,γ2,γ3,γ4,γ5,γ6,γ7,γ8,γ9,γ10,并且和筆算進行檢驗通過計算機計算可得到相關結果如圖1所示。
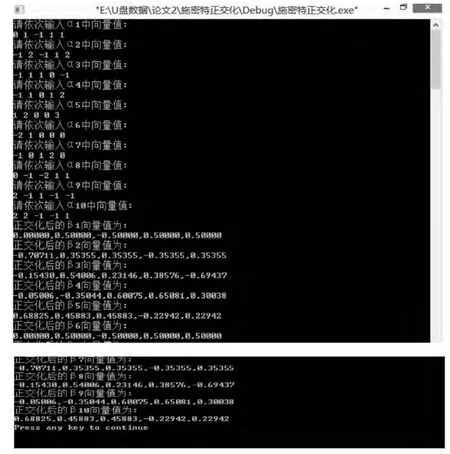
圖1 標準化正交向量組結果Fig.1 The result of standardized orthogonal vectors
4 結論
文中通過比較兩種正交化的計算方法人工計算和語言執行[5-6]。很明顯,使用語言編寫其函數包,便于應用工作者使用,豐富了語言的知識和擴充了語言中的函數包,計算簡單,簡化了計算量,提高了工作效率。計算不容易出錯,并且計算精度調至計算穩定,隨著計算過程逐步積累,誤差[7-8]較小,是可用的計算結果。
[1]徐仲,陸全,張凱院.高等代數考研教案第[M].西安:西北工業大學出版社,2009.
[2]王萼芳,石生明.北京大學數學系幾何與代數教研室前代數小組[M].北京:高等教育出版社,2005.
[3]古萬榮.Visual C++輕松入門[M].北京:人民郵電出版社,2010.
[4]Steven leon.Linear Alegebra with Applications Sixth Edition[M].Beijing:China Machine Press,2004.
[5]羅朝盛,鄭玲利.Visual Basic6.0程序設計[M].北京:清華大學出版社,2011.
[6]王家文,李仰軍.MATLAB7.0圖像處理[M].長沙:國防工業大學出版社,2006.
[7]趙建軍,姚剛,王毅,等.某測量系統誤差源分析及建模[J].現代電子技術,2014(1):38-40.ZHAO Jian-jun,YAO Gang,WANG Yi,et al.Analysis and modeling of one measuring system error source[J].Modern Electronics Technique,2014(1):38-40.
[8]張晏旭,吳鐵柱.高速數傳信號角跟蹤及誤差分析[J].電子科技,2012(11):52-54.ZHANG Yan-xu,WU Tie-zhu.Angel tracking and error analysis for the high speed data transmitting signal[J].Electronic Science and Technology,2012(11):52-54.

