基于GA－LSSVR算法的回采工作面瓦斯涌出量預測

曹慶奎，商娜欣

(河北工程大學經濟管理學院，河北邯鄲056038)

針對瓦斯涌出量的預測現已形成了多種理論和方法［1］:呂伏等［2］利用多元統計學中的主成分分析方法對回采工作面的瓦斯涌出量進行了多步線性回歸預測，結果表明該方法具有較好的精確度;王生全等［3］和朱紅青等［4］針對瓦斯涌出量建立了BP神經網絡預測模型，并與遺傳算法相結合進行了瓦斯涌出量的預測;邵良杉等［5－6］將小波框架理論引入到支持向量機預測函數中，利用小波變換將輸入向量映射到一個高維特征空間從而利用支持向量機進行預測;王曉路等［7］提出了一種基于虛擬狀態變量的卡爾曼濾波瓦斯涌出量預測模型，該模型有較好的跟蹤能力和反應速度;孫林等［8］基于結構風險最小化的原則提出了一種基于最小二乘支持向量機的回采工作面瓦斯涌出量的預測方法;陶云奇等［9－10］建立了改進的灰色馬爾柯夫模型，對工作面絕對瓦斯涌出量進行了預測;谷松等［11］和伍愛友等［12］將灰色系統理論應用到瓦斯涌出量的預測當中，結果表明預測結果較為理想;曹慶奎等［13］針對礦井工作面瓦斯涌出量進行了未確知聚類研究，較好的解決了礦井瓦斯涌出量的分類問題，對瓦斯涌出量的預測提供了分類方法。本文將遺傳算法和最小二乘支持向量回歸機相結合，利用遺傳算法對最小二乘支持向量回歸的參數進行優化，建立回采工作面瓦斯涌出量的預測模型，并以實例驗證其有效性。

1 最小二乘支持向量回歸機

最小二乘支持向量回歸機(least squares support vector regression，簡稱LSSVR)通過構造回歸函數來解決預測問題，通過一個非線性映射函數將輸入樣本數據映射到高維特征空間，然后在此空間進行回歸預測［14］，與支持向量回歸機(support vector regression，簡稱 SVR)有所不同，LSSVR構造了一個新的二次損失函數，將SVR的二次規劃問題轉變為求解線性方程問題，可以有效的增加回歸精度和計算速度［15］。

訓練樣本集為D={(xi，yi)|i=1，2，…，n}，其中xi為輸入數據，yi為輸出數據。

LSSVR的優化問題為

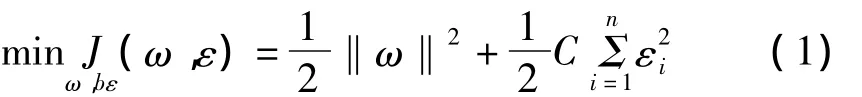
約束條件為

式中C－懲罰參數;ω－權向量;b－閾值;εi－誤差。

引入拉格朗日乘子ai，將問題轉化為

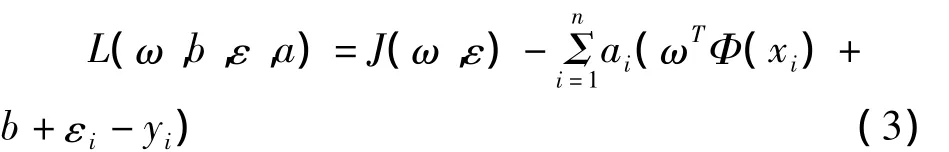
對(3)式中 ω、b、εi、和 αi分別求偏導數，可以得到

黃宗羲“一本而萬殊”的生態共同體論，在以氣貫通天人，強調“存有的連續性”[5](P160)的同時，從氣異性異出發，將宋明諸儒說明人性的氣質之性與義理之性，根據稟氣之精粗清濁分屬人與物。對物而言，只可言氣質之性，故氣質之性即物性。對人而言，人只有義理之性；同時，義理之性不離氣質，故人的氣質的性即義理之性。這不但克服了張載以來的人性二元論，也使得程朱理學從理上分殊人、物之性的“理一分殊”論，轉化成了氣異性異的“一本萬殊”論。總之，黃宗羲“一本而萬殊”的生態共同體論，既深化了儒家以天人關系為核心問題的生態意識，也強化了儒家以參贊化育為目的的德性修養所蘊含的生態責任。

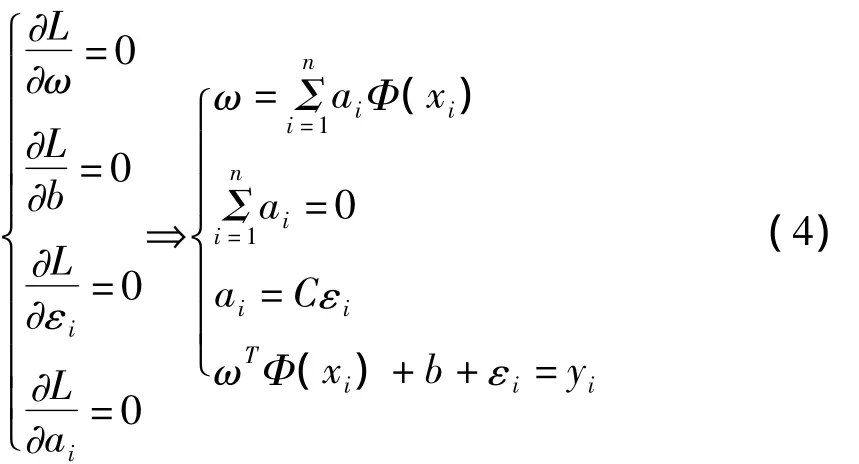
消除ω和εi，得到線性方程組

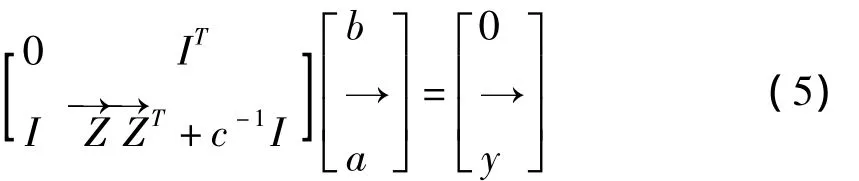
2 遺傳—最小二乘支持向量回歸模型

為了使LSSVR的預測性能更好，就需要獲得較優的C，δ，ε參數組合，這樣才能使預測結果更加靠近實際真實值［16］，因此需要利用遺傳算法(Genetic Algorithm，GA)對參數C，δ，ε 進行優化，因為GA具有非常強的全局搜索能力，能夠有效的模擬生物進化過程中的自然選擇和遺傳變異，可以有效的優化參數，因此可以利用這一優點對LSSVR中的參數進行優化，從而構造遺傳—最小二乘支持向量回歸模型(GA－LSSVR)，具體的操作步驟如圖1所示。

(1)選擇LSSVR的訓練樣本數據集，形成初始化LSSVR數據集。

(2)利用GA對參數進行編碼。在編碼過程中采取實數編碼方式，可以有效的提高GA的求解速度和性能，能夠有效的求解復雜的連續參數優化問題。

(3)對初始參數種群進行訓練，訓練過程中調用LSSVR算法。

(4)計算GA適應度。適應度函數定義為訓練數據上的交叉驗證后的均方誤差平均值為:

式中l－訓練集的樣本數;yi－第i個樣本的實際值;fi－第i個樣本的預測值。

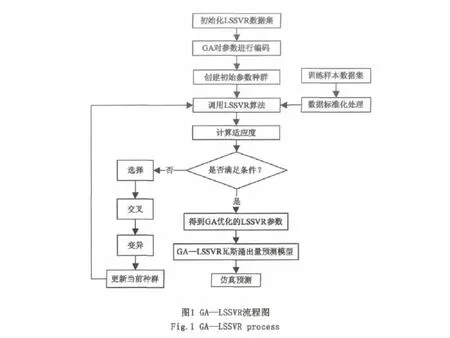
(5)進行遺傳操作。根據計算出的GA的適應度，對群體進行遺傳操作，即選擇、交叉、變異操作，對種群進行更新，然后進行步驟(3)，調用LSSVR算法進行操作。

(6)停止訓練。如果滿足GA訓練的停止條件則停止訓練，即得到了最優的LSSVR參數，如果不滿足停止條件，則進行步驟(3)，繼續對參數進行優化和訓練。

(7)進行預測和仿真。將經過GA訓練以后已經優化了的LSSVR參數進行預測，利用GALSSVR預測模型進行預測，并進行仿真預測，測驗結果。

3 案例分析

3.1 樣本數據的選擇

在文獻［2］中選取15個典型的回采工作面瓦斯涌出資料，其中前12個用于GA訓練樣本，另外3個作為GA－LSSVR算法的測試樣本。原始煤層數據參數有 10 個［2］:瓦斯含量(m3/t)、深度(m)、厚度(m)、工作面長度(m)、推進速度(m/min)、采出率(%)、鄰近層瓦斯含量(m3/t)、鄰近層厚度(m)、開采深度(m)、瓦斯涌出量(m3/t)。15個典型的回采工作面煤層賦存條件以及瓦斯涌出情況見表1。

在進行預測時需要將原始數據進行標準化處理，可免除不同量綱對數據產生的不利影響，在進行標準化處理時采用統計學中的比例轉換法，正向指標轉換公式為x'=(x－xmin)/(xmax－xmin)，逆向指標轉換公式為x'=(xmax－x)/(xmax－xmin)。標準化以后的樣本數據見表2。

3.2 參數選擇與優化

利用GA訓練樣本參數，確定GA中種群規模、進化代數、交叉變異概率的數值以及各種參數的取值范圍見表3。

利用 matlab7.0 優化工具軟件［17］，將表 1 中的GA訓練樣本中前12組數據中的瓦斯含量、深度、厚度、工作面長度、推進速度、采出率、鄰近層瓦斯含量、鄰近層厚度、層間距、開采深度11個參數向量作為訓練函數的輸入向量，瓦斯涌出量作為目標向量，輸入到GA中進行訓練，結束訓練后即可得到GA－LSSVR預測模型的最優的參數，懲罰參數C為 20.309，徑向基核函數參數 δ為10.02，不敏感損失函數 ε 為0.135。

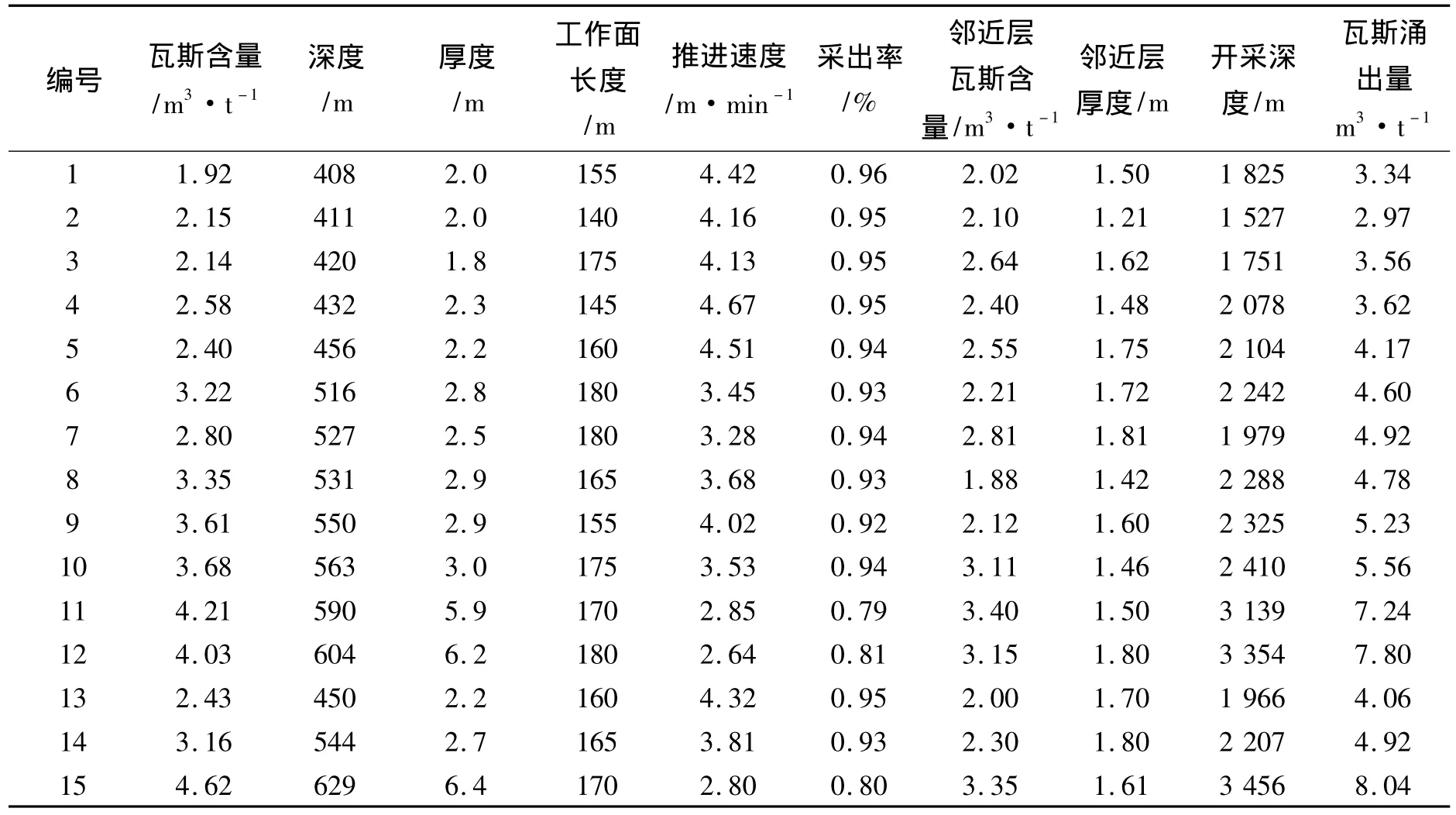
表1回采工作面煤層賦存條件及瓦斯涌出量原始數據Tab.1 The raw data of the gas emission quantity of the working face

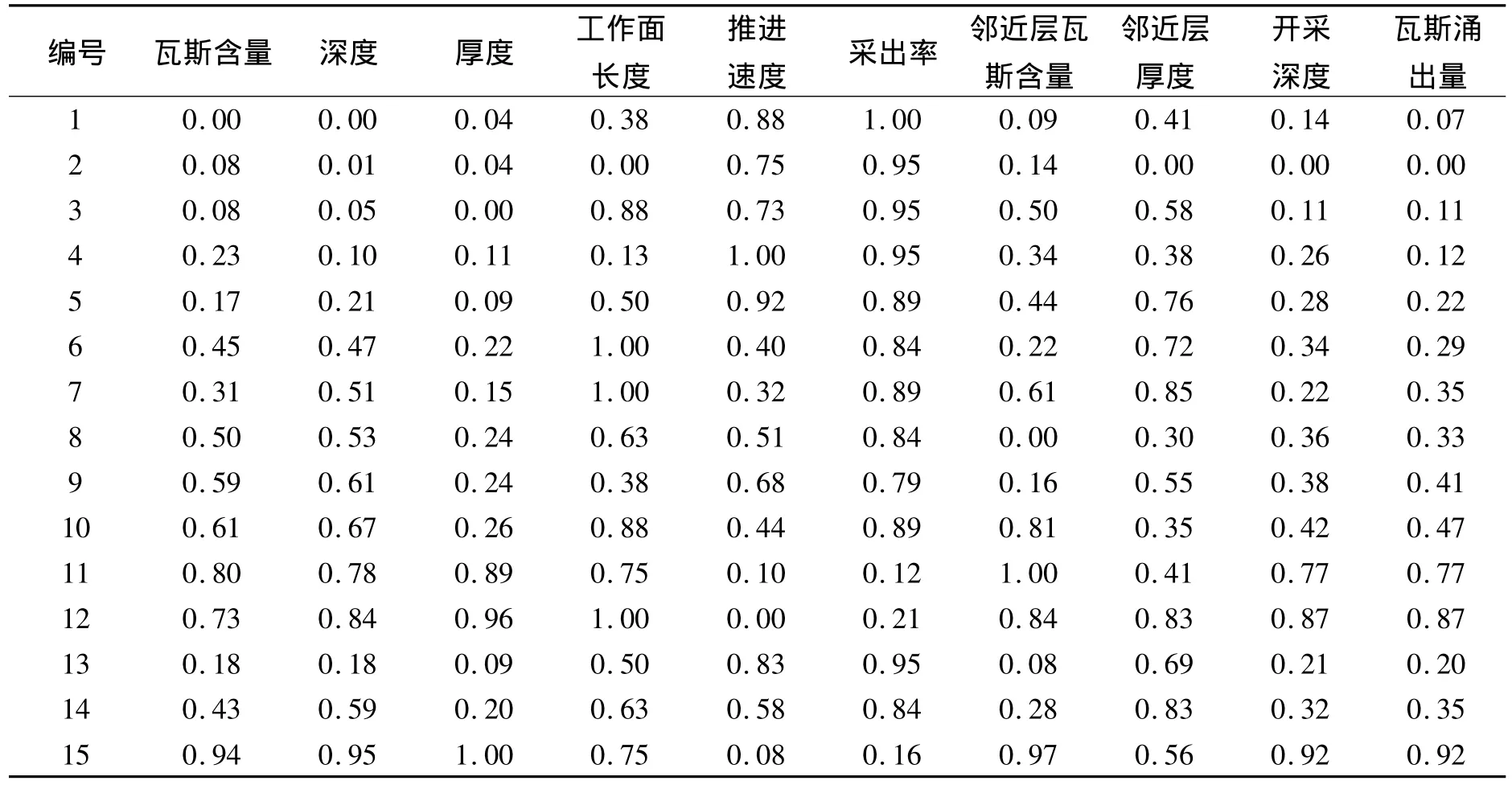
表2回采工作面瓦斯涌出量原始數據標準化Tab.2 The raw data of the gas emission quantity of the working face

表3 GA參數選擇Tab.3 The data of the GA

3.3 測試樣本的瓦斯涌出量預測

經過訓練可以得到最優的參數，利用最優參數可以對瓦斯涌出量的測試樣本進行測試，可以得到相關的預測值，然后對預測值進行適當的處理，將其反歸一化。然后將GA－LSSVR預測模型得到結果與SVR模型進行預測得到的結果進行比較，得出比較的結果見表4。

表4不同預測模型下瓦斯涌出量預測值對比Tab.4 Comparison of the prediction values of gas emission quantity from different models

4 結論

將遺傳算法和最小二乘支持向量回歸機相結合能夠有效的進行瓦斯涌出量的預測，測試的結果可以看出GA－LSSVR預測效果是最好的，在模型數據的運行過程中，GA－LSSVR預測模型計算速度更快，預測的誤差更小，更接近于真實值，為以后的回采工作面瓦斯涌出量預測提供一個有效可行的方法。

［1］瓦斯通風防滅火安全研究所.礦井瓦斯涌出量預測方法的發展與貢獻［J］.煤炭安全，2003，34(9):10－13.

［2］呂伏，梁冰，等.基于主成分回歸分析法的回采工作面瓦斯涌出量預測［J］.煤炭學報，2012，37(1):113－116.

［3］王生全，劉柏根，張召召，等.遺傳算法的BP網絡模型進行瓦斯涌出量預測［J］.西安科技大學學報，2012，32(1):51－56.

［4］朱紅青，常文杰，張 彬.回采工作面瓦斯涌出BP神經網絡分源預測模型及應用［J］.煤炭學報，2007，32(5):504－508.

［5］邵良杉，張 宇.基于小波理論的支持向量機瓦斯涌出量的預測［J］.煤炭學報，2011，36(1):104 －107.

［6］焦春林，傅雪海，葛燕燕，等.我國煤礦瓦斯中H2S異常礦井的分布特征［J］.黑龍江科技學院學報，2013，23(4):375－377.

［7］王曉路，劉 健，盧建軍.基于虛擬狀態變量的卡爾曼濾波瓦斯涌出量預測［J］.煤炭學報，2011，36(1):80－85.

［8］孫林，楊世元.基于LS－SVM的回采工作面瓦斯涌出量預測［J］.煤炭學報，2008，33(12):1377－1381.

［9］陶云奇，許江，李樹春.改進的灰色馬爾柯夫模型預測采煤工作面瓦斯涌出量［J］.煤炭學報，2007，32(4):391－395.

［10］張迎新，孫浩.基于ANSYS溫度場的煤層瓦斯壓力模擬可行性［J］.黑龍江科技學院學報，2013，23(4):333－336.

［11］谷 松，崔洪慶，馮文麗.基于灰色理論的小波神經網絡對瓦斯涌出量的預測［J］.煤炭學報，2007，32(9):964－967.

［12］王麗華.基于GA－LSSVR的圖書館文獻資源需求預測［J］.計算機應用與軟件，2011，28(6):225 －227.

［13］曹慶奎，任向陽，劉開第.礦井工作面瓦斯涌出量的未確知聚類研究［J］.煤炭學報，2006，31(3):337 －341.

［14］郭志明，陳立平，黃文倩，等.近紅外光譜結合GALSSVR分析煙草尼古丁含量［J］.激光與電子學進展，2012，49(3):1 －5.

［15］趙清艷，張 超.基于GA－LSSVR的銑削加工變形預測［J］.組合機床與自動化加工技術，2011，12(4):57－60.

［16］薛定宇，陳陽泉.高等應用數學問題的MATLABE求解［M］.北京:清華大學出版社，2012.

［17］SHAO LIANG SHAN，FU GUI XIANG.Disaster prediction of coal mine gas based on data mining［J］.Journal of Coal Science＆ Engineering(China)，2008，14(3):458－463.