帶靜態(tài)參數(shù)的高超聲速飛行器軌跡優(yōu)化算法

張紅文

(北京航空航天大學(xué) 宇航學(xué)院，北京 100191)

張科南

(北京機(jī)電工程研究所，北京 100074)

陳萬(wàn)春

(北京航空航天大學(xué) 宇航學(xué)院，北京 100191)

飛行器軌跡優(yōu)化問(wèn)題本質(zhì)上是一個(gè)最優(yōu)控制問(wèn)題.通常的軌跡優(yōu)化問(wèn)題是一個(gè)動(dòng)態(tài)優(yōu)化過(guò)程.通過(guò)對(duì)動(dòng)態(tài)參數(shù)(如控制變量、狀態(tài)變量等)的尋優(yōu)，獲得滿足極值條件的解.隨著工程設(shè)計(jì)系統(tǒng)化的加強(qiáng)、復(fù)雜性的增加，單純的動(dòng)態(tài)優(yōu)化越來(lái)越不能滿足總體設(shè)計(jì)的要求，有許多靜態(tài)參數(shù)也需要隨著動(dòng)態(tài)參數(shù)的優(yōu)化而優(yōu)化，以獲得全局最優(yōu)的軌跡.在動(dòng)態(tài)優(yōu)化中，所有不隨時(shí)間變化的參數(shù)均可作為優(yōu)化變量進(jìn)行優(yōu)化.例如動(dòng)態(tài)優(yōu)化中的初始參數(shù)、終端參數(shù)、飛行時(shí)間和過(guò)程約束量等，以及與軌跡密切相關(guān)的飛行器總體參數(shù)或者叫設(shè)計(jì)變量，如起飛重量、推進(jìn)系統(tǒng)設(shè)計(jì)參數(shù)和氣動(dòng)外形特性參數(shù)等［1］.本文稱這一類問(wèn)題為帶靜態(tài)參數(shù)的軌跡優(yōu)化問(wèn)題.

關(guān)于動(dòng)態(tài)軌跡優(yōu)化問(wèn)題的研究，學(xué)者們已經(jīng)取得了豐富的研究成果.尤其是在直接法領(lǐng)域，計(jì)算機(jī)技術(shù)的飛速發(fā)展為直接法的應(yīng)用提供了有利條件.

Gauss偽譜法［2－3］是近年來(lái)比較熱門(mén)的一種正交配點(diǎn)算法.其收斂速度快，魯棒性好，并且能夠得到間接法才能獲得的協(xié)態(tài)變量信息.對(duì)于帶靜態(tài)參數(shù)的軌跡優(yōu)化問(wèn)題，只有為數(shù)不多的幾篇文獻(xiàn)可供參考.文獻(xiàn)［4］提出了靜態(tài)動(dòng)態(tài)混雜優(yōu)化方法，將靜態(tài)參數(shù)看作導(dǎo)數(shù)為零的狀態(tài)變量，推導(dǎo)出了廣義的一階必要條件，但是沒(méi)有給出算例，也沒(méi)有提供兩點(diǎn)邊值問(wèn)題(TPBVP，Two-Point Boundary Value Problem)的數(shù)值求解方法.Hull在其著作中對(duì)最優(yōu)控制中的靜態(tài)參數(shù)進(jìn)行了研究［5］，同樣將這些靜態(tài)參數(shù)加入原系統(tǒng)中，構(gòu)成增廣系統(tǒng)，通過(guò)求變分，給出了最優(yōu)一階和二階條件.Hull提供了幾個(gè)簡(jiǎn)單算例，將終端時(shí)間作為靜態(tài)參數(shù)進(jìn)行處理，得到了解析解，但也沒(méi)有給出TPBVP的數(shù)值算法.

本文在文獻(xiàn)［4－5］的基礎(chǔ)上，總結(jié)并給出了靜態(tài)參數(shù)是飛行時(shí)間，初始、終端狀態(tài)參數(shù)，以及設(shè)計(jì)變量幾種情況下的最優(yōu)一階條件.同時(shí)利用Gauss偽譜法提供的協(xié)態(tài)變量信息，提出了求解TPBVP的一種新算法.該算法結(jié)合了直接法和間接法的優(yōu)點(diǎn)，具有收斂速度快，計(jì)算精度高的優(yōu)點(diǎn)，完成一條實(shí)際飛行時(shí)間2 000 s的軌跡優(yōu)化計(jì)算只需要數(shù)秒鐘時(shí)間.最后，以乘波體為研究對(duì)象，給出了一個(gè)氣動(dòng)外形/軌跡一體化優(yōu)化設(shè)計(jì)算例，驗(yàn)證了本文方法的有效性.

1 最優(yōu)控制問(wèn)題描述

1.1 一般最優(yōu)控制問(wèn)題描述

最常見(jiàn)的是固定起點(diǎn)、終端時(shí)間未定的最優(yōu)控制問(wèn)題，即Bolza問(wèn)題，設(shè)系統(tǒng)狀態(tài)方程為

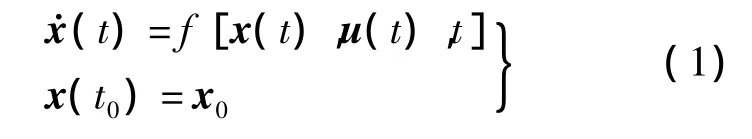
式中，狀態(tài)變量x(t)∈Rn;控制變量u(t)∈Rm，目標(biāo)函數(shù)為

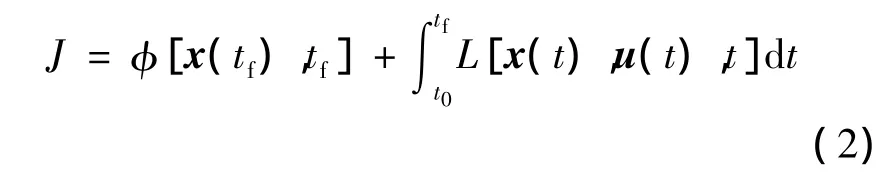
終端狀態(tài)變量需滿足約束:

求解上述問(wèn)題時(shí)，引入拉格朗日乘子λ(t)和ν，構(gòu)造增廣目標(biāo)函數(shù)如下:

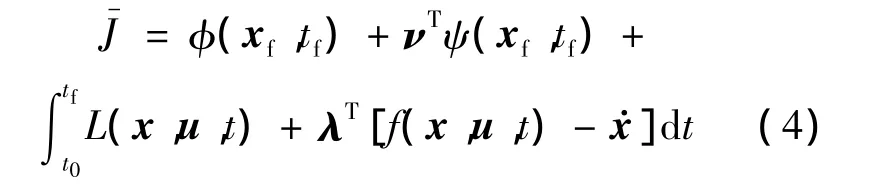
定義哈密頓函數(shù):

增廣終端約束函數(shù):

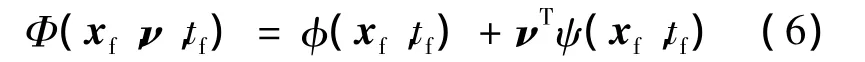
狀態(tài)方程:

協(xié)態(tài)方程:

控制方程:

邊界條件:

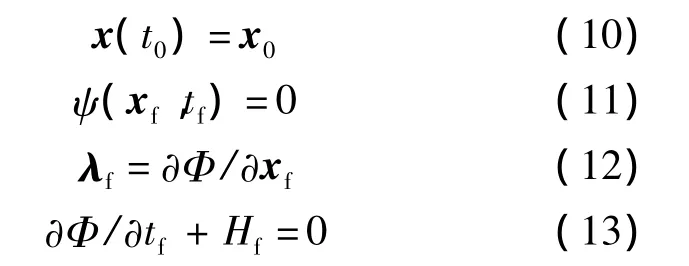
式(7)～式(13)構(gòu)成了一般最優(yōu)控制問(wèn)題的一階優(yōu)化必要條件.

1.2 帶靜態(tài)參數(shù)的最優(yōu)控制問(wèn)題

按照在軌跡優(yōu)化過(guò)程中應(yīng)用，將靜態(tài)參數(shù)分為3類:終端時(shí)間、起始或終端狀態(tài)變量和設(shè)計(jì)變量.

1.2.1 靜態(tài)參數(shù)為終端時(shí)間

為了方便兩點(diǎn)邊值問(wèn)題求解，需要將自由終端時(shí)間問(wèn)題轉(zhuǎn)換為固定終端時(shí)間問(wèn)題，引入無(wú)量綱時(shí)間變量τ:

于是1.1節(jié)的最優(yōu)控制問(wèn)題中，目標(biāo)函數(shù)式變形為

對(duì)應(yīng)的一階必要條件狀態(tài)方程式、協(xié)態(tài)方程式分別變形為

其余條件不變.此時(shí)，終端時(shí)間成為了優(yōu)化過(guò)程中的一個(gè)未知靜態(tài)變量，式(13)是用來(lái)求解未知終端時(shí)間的方程.

1.2.2 靜態(tài)參數(shù)為邊界點(diǎn)狀態(tài)變量

考慮更一般的情況，初始時(shí)間和初始狀態(tài)不再固定，假設(shè)初始條件約束為

引入拉格朗日乘子ξ，將終端約束式增廣為端點(diǎn)約束:

得到新的增廣目標(biāo)函數(shù)為

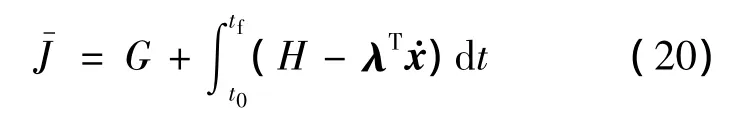
同樣對(duì)該目標(biāo)函數(shù)取變分后，得到新的一階必要條件，其中狀態(tài)方程、協(xié)態(tài)方程和控制方程形式未變，邊界條件增加兩個(gè)方程式:式(21)和式(22)，式(21)提供了未知初始狀態(tài)變量的協(xié)態(tài)初值，式(22)用來(lái)求解未知的初始時(shí)間.

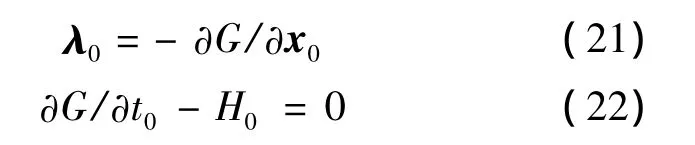
1.2.3 靜態(tài)參數(shù)為設(shè)計(jì)變量

動(dòng)態(tài)軌跡優(yōu)化過(guò)程中，有時(shí)需要考慮一些設(shè)計(jì)變量的優(yōu)化，例如飛行器起飛重量、氣動(dòng)外形幾何參數(shù)等.

按照1.2.1節(jié)的方法，一般的自由終端時(shí)間問(wèn)題均可以轉(zhuǎn)換為固定終端時(shí)間問(wèn)題，假設(shè)p表示優(yōu)化過(guò)程中的設(shè)計(jì)變量，帶設(shè)計(jì)參數(shù)的固定終端時(shí)間優(yōu)化問(wèn)題的目標(biāo)函數(shù)可以表示如下:

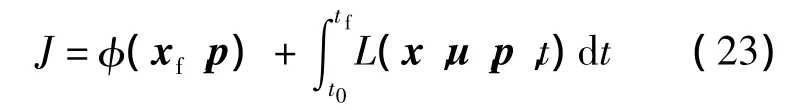
引入方程:

則可以將設(shè)計(jì)參數(shù)p看作狀態(tài)變量.由于p不隨時(shí)間變化，p的兩個(gè)端點(diǎn)值可以認(rèn)為是自由的，這樣，該問(wèn)題可以看作是狀態(tài)變量p初始值和終端值自由的最優(yōu)控制問(wèn)題.

式(23)改寫(xiě)為

其中，p=p0=pf.此時(shí)最優(yōu)控制問(wèn)題的一階優(yōu)化條件有如下改動(dòng).

狀態(tài)方程擴(kuò)維:

協(xié)態(tài)方程擴(kuò)維:

控制方程形式不變，邊界條件也需要進(jìn)行擴(kuò)維處理，添加關(guān)于p的兩個(gè)方程:

其余邊界條件與一般最優(yōu)控制問(wèn)題中相同.

2 最優(yōu)控制問(wèn)題求解

最優(yōu)控制問(wèn)題的一階必要條件構(gòu)成了一個(gè)兩點(diǎn)邊值問(wèn)題.關(guān)于兩點(diǎn)邊值問(wèn)題的求解，目前主要有打靶法、差分法和有限元法等幾種算法［6］.不管采用哪種算法，都需要對(duì)兩點(diǎn)邊值問(wèn)題的初值進(jìn)行估計(jì)，如果估計(jì)不準(zhǔn)確，則很難得到理想的解.這是求解兩點(diǎn)邊值問(wèn)題的難點(diǎn)所在.因?yàn)樽顑?yōu)控制問(wèn)題中的協(xié)態(tài)變量沒(méi)有明顯的物理意義，協(xié)態(tài)變量初值估計(jì)一直以來(lái)都是一個(gè)研究難點(diǎn).不過(guò)，近年來(lái)對(duì)偽譜法研究發(fā)現(xiàn)，這種新的直接法不但收斂速度快，而且滿足協(xié)態(tài)映射定理，可以提供最優(yōu)控制問(wèn)題的協(xié)態(tài)信息.于是，本文提出一個(gè)求解兩點(diǎn)邊值問(wèn)題的新思路:先用Gauss偽譜法進(jìn)行求解，獲得次優(yōu)解，包括狀態(tài)變量、協(xié)態(tài)變量.以次優(yōu)解作為兩點(diǎn)邊值問(wèn)題的初始參考，利用基于有限元法的邊值問(wèn)題求解器進(jìn)行計(jì)算.

2.1 協(xié)態(tài)映射原理

根據(jù)Gauss偽譜方法轉(zhuǎn)換后得到的非線性規(guī)劃(NLP，Non-Linear Programming)問(wèn)題的 KKT(Karush-Kuhn-Tucker)條件，跟原Bolza問(wèn)題的連續(xù)一階必要條件利用Gauss離散之后的形式是完全等效的［3］.

協(xié)態(tài)映射原理說(shuō)明，求解Gauss偽譜轉(zhuǎn)換后的NLP問(wèn)題與求解利用Gauss偽譜方法離散的最優(yōu)控制一階必要條件是等價(jià)的.前者是直接方法，后者是間接方法.兩者間的關(guān)系如圖1所示.

圖1 Gauss偽譜轉(zhuǎn)換方法

理論上，只要設(shè)置足夠多的Gauss點(diǎn)，Gauss偽譜方法轉(zhuǎn)換后的NLP問(wèn)題的解是滿足最優(yōu)一階必要條件的.然而，在實(shí)際應(yīng)用過(guò)程中，隨著Gauss點(diǎn)的增多，優(yōu)化變量越來(lái)越多，運(yùn)算速度大幅度下降，而且對(duì)于像飛行器軌跡優(yōu)化這類復(fù)雜的非線性優(yōu)化問(wèn)題，NLP求解器往往不容易收斂到最優(yōu)解.故本文將Gauss偽譜方法作為最優(yōu)解初值生成的手段，這樣精度要求不高，可以利用比較少的Gauss點(diǎn)，快速獲得次優(yōu)解.

2.2 兩點(diǎn)邊值問(wèn)題計(jì)算

為求解邊值問(wèn)題，Matlab軟件提供了一個(gè)bvp4c的函數(shù)文件［7］.該文件是依據(jù)有限元法編寫(xiě)而成.解題的基本思路如下.

1)首先把待解問(wèn)題轉(zhuǎn)化為標(biāo)準(zhǔn)邊值問(wèn)題:

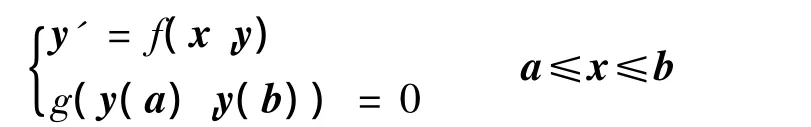
2)因?yàn)檫呏祮?wèn)題可以多解，所以需要一個(gè)初始猜測(cè).該猜測(cè)網(wǎng)包括區(qū)間［a，b］內(nèi)的一組網(wǎng)格點(diǎn)和網(wǎng)格點(diǎn)上的解S(x).

3)根據(jù)原微分方程構(gòu)造殘差函數(shù):顯然，當(dāng)猜測(cè)解S(x)等于真解y(x)時(shí)，有殘差r(x)=0，邊值g(S(a)，S(b))=0.S(x)不是真解，殘差不為零.

4)利用原微分方程和邊界條件，借助迭代不斷產(chǎn)生新的S(x)，使殘差不斷減小，從而獲得滿足精度要求的解.

整個(gè)求解過(guò)程中，第2)步初始猜測(cè)是很關(guān)鍵的.如果初始猜測(cè)離真解太遠(yuǎn)，則迭代求解無(wú)法進(jìn)行.

根據(jù)Gauss偽譜方法解的特點(diǎn)，選擇Gauss點(diǎn)作為初始猜測(cè)網(wǎng)格點(diǎn)，而對(duì)應(yīng)的每個(gè)網(wǎng)格點(diǎn)上的狀態(tài)變量和協(xié)態(tài)變量的值作為初始猜測(cè)網(wǎng)格點(diǎn)上的解，從而構(gòu)成一個(gè)完整的初始猜測(cè)，并且該猜測(cè)十分接近最優(yōu)解，能夠保證迭代的順利進(jìn)行.

3 算例分析

以乘波體研究對(duì)象，將氣動(dòng)外形參數(shù)作為靜態(tài)優(yōu)化參數(shù)，優(yōu)化求解全局最大航程問(wèn)題.

3.1 乘波體簡(jiǎn)介

文獻(xiàn)［8］提出了一種全新的高超聲速飛行器布局，因?yàn)槭怯梢环N已知的超聲速或高超聲速流場(chǎng)生成的氣動(dòng)構(gòu)型，在設(shè)計(jì)點(diǎn)成波體的整個(gè)前緣產(chǎn)生貼附的激波，整個(gè)構(gòu)型像是騎在激波面上，所以被稱為乘波體(waverider)，或稱乘波構(gòu)型，如圖2所示.

圖2 圓錐繞流場(chǎng)及錐導(dǎo)乘波體示意圖

3.2 乘波體外形參數(shù)選擇

錐導(dǎo)乘波體的外形設(shè)計(jì)是從給定最初的高超聲速流場(chǎng)開(kāi)始的，因此流場(chǎng)參數(shù)、激波形狀和乘波體在流場(chǎng)中的位置都對(duì)乘波體的外形有直接的影響，如圖2所示.

通過(guò)實(shí)驗(yàn)設(shè)計(jì)分析發(fā)現(xiàn)，對(duì)外形影響最大的參數(shù)主要有4 個(gè):Macfg，βcfg，XL，ω.而這其中又屬ω對(duì)形狀的影響最明顯，為降低間接法求解難度，本文中將問(wèn)題進(jìn)行簡(jiǎn)化，只研究ω的變化對(duì)外形的影響，固定其余3個(gè)參數(shù).這樣，外形優(yōu)化參數(shù)就只有一個(gè)了，即ω.

3.3 氣動(dòng)系數(shù)計(jì)算

一旦外形確定以后，便可以進(jìn)行氣動(dòng)系數(shù)的計(jì)算［9－10］.本文選用基于高速無(wú)粘流理論的氣動(dòng)工程計(jì)算方法——牛頓面元法［11］，進(jìn)行氣動(dòng)估算.

間接法求解，需要得到氣動(dòng)系數(shù)的解析表達(dá)式.為此，首先利用牛頓面元法計(jì)算多種工況下乘波體氣動(dòng)力系數(shù)，然后利用響應(yīng)面方法(RSM，Response Surface Method)［12］將離散的氣動(dòng)數(shù)據(jù)代理為解析多項(xiàng)式形式.

乘波體底部出口型線高寬比的變化范圍為

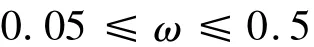
高寬比的變化將引起底部厚度以及整個(gè)乘波體長(zhǎng)度的變化;其余3個(gè)外形參數(shù)固定，其中Macfg=10，βcfg=12°，XL= －19.5m.攻角變化范圍－5°≤α≤20°，擬合以后得到的響應(yīng)面多項(xiàng)式為

3.4 質(zhì)量和參考面積計(jì)算

乘波體外形確定以后，其質(zhì)量和參考面積可以通過(guò)估算公式獲得.

總質(zhì)量可以通過(guò)下式估算.

氣動(dòng)參考面積Sref取乘波體XY平面的投影面積.本文中外形參數(shù)只有高寬比一個(gè)，故可以將總質(zhì)量和參考面積擬合為高寬比的函數(shù):

3.5 動(dòng)力學(xué)方程

只考慮乘波體在縱平面內(nèi)的運(yùn)動(dòng)，動(dòng)力學(xué)方程如下:

式中，r為飛行器質(zhì)心到地心的距離;V為對(duì)地速度;γ為航跡角;θ為經(jīng)度.

大氣密度采用簡(jiǎn)化模型:

式中，ρ0為海平面大氣密度;h為飛行器距當(dāng)?shù)睾Ｆ矫娴母叨龋琱=r－R0，R0為地球半徑;常數(shù)H0=7200m.

3.6 間接法求解過(guò)程及結(jié)果

目標(biāo)函數(shù)均為使航程最大化，假定飛行器只在縱平面內(nèi)運(yùn)動(dòng)，可以表示為縱程最大化:

初始條件和終端條件如表1所示.

表1 乘波體外形/軌跡兩層優(yōu)化邊界條件

優(yōu)化過(guò)程中，將ω看作狀態(tài)變量，故系統(tǒng)的狀態(tài)方程除了式(35)～式(38)以外，還需添加一個(gè)的有效范圍為0.05≤ω≤0.5.

對(duì)應(yīng)地引入新的協(xié)態(tài)變量λω，哈密頓函數(shù)寫(xiě)為

增加一個(gè)協(xié)態(tài)方程:

控制表達(dá)式為

經(jīng)過(guò)整理后有

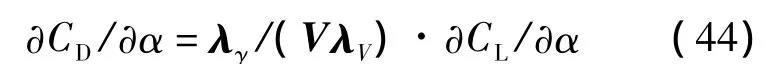
另外，終端時(shí)間自由對(duì)應(yīng)的橫截條件:

最后，協(xié)態(tài)邊界條件

該系統(tǒng)共有5個(gè)狀態(tài)變量5個(gè)協(xié)態(tài)變量，對(duì)應(yīng)5個(gè)狀態(tài)方程5個(gè)協(xié)態(tài)方程和10個(gè)邊界條件，另外，式(43)和式(45)分別決定了控制量和飛行時(shí)間，構(gòu)成了一個(gè)標(biāo)準(zhǔn)兩點(diǎn)邊值問(wèn)題.求解該兩點(diǎn)邊值問(wèn)題，得到乘波體最優(yōu)高寬比:

對(duì)應(yīng)的最佳外形如圖3所示，對(duì)應(yīng)的最大航程為13 082 km，最優(yōu)軌跡曲線如圖4～圖7所示.

為了驗(yàn)證結(jié)果的合理性，固定外形參數(shù)ω，分別進(jìn)行多次單層動(dòng)態(tài)軌跡優(yōu)化，如圖8所示，可見(jiàn)，隨著ω的增加，最大航程先是越來(lái)越大，后又逐漸變小，即ω存在一個(gè)極值點(diǎn)對(duì)應(yīng)全局最大航程.

圖3 最優(yōu)高寬比對(duì)應(yīng)的乘波體外形

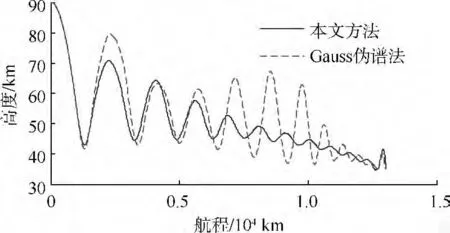
圖4 外形/軌跡一體優(yōu)化的最大航程軌跡

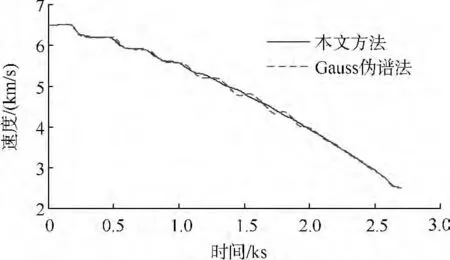
圖5 外形/軌跡一體優(yōu)化的速度曲線

圖6 外形/軌跡一體優(yōu)化的控制變量

圖7 外形/軌跡一體優(yōu)化的外形參數(shù)協(xié)態(tài)曲線

圖8a中的最優(yōu)軌跡曲線代表相應(yīng)的全局最大航程軌跡.

圖8b中列出了不同的ω對(duì)應(yīng)的終端航程，最優(yōu)高寬比 ω*=0.3381.

圖8 不同高寬比對(duì)應(yīng)的最大航程軌跡

圖8給出了ω=0.05～0.5對(duì)應(yīng)的最大航程軌跡.可見(jiàn)，隨著高寬比的增加，乘波體外形由寬短型向細(xì)長(zhǎng)型發(fā)展，對(duì)應(yīng)的最大航程先越來(lái)越大，當(dāng)高寬比超過(guò)最優(yōu)值后又開(kāi)始變小，這說(shuō)明高寬比對(duì)航程的影響很大，恰當(dāng)?shù)母邔挶饶軌虺浞职l(fā)揮飛行器的潛能.

4 結(jié)論

本文給出了一種求解帶靜態(tài)參數(shù)最優(yōu)控制問(wèn)題的間接法數(shù)值算法，并成功地應(yīng)用在了乘波體的最大航程軌跡優(yōu)化中.

文中將靜態(tài)參數(shù)分為了3類:終端時(shí)間、邊界點(diǎn)狀態(tài)變量和設(shè)計(jì)變量.針對(duì)不同的靜態(tài)參數(shù)，給出了對(duì)應(yīng)的一階最優(yōu)必要條件.數(shù)值算法結(jié)合了直接法和間接法的優(yōu)點(diǎn)，利用Gauss偽譜方法滿足協(xié)態(tài)映射原理的特點(diǎn)，將Gauss偽譜方法的優(yōu)化結(jié)果作為間接法數(shù)值求解器的初始猜測(cè)，可以高效而精確地得到最優(yōu)解，通常只需要數(shù)秒鐘便可以完成一條彈道的優(yōu)化計(jì)算.以乘波體為研究對(duì)象，給出了靜態(tài)參數(shù)外形高寬比的最大航程優(yōu)化算例，結(jié)果顯示外形參數(shù)對(duì)最大航程的影響很大，隨著高寬比的增加，乘波體外形由寬短型向細(xì)長(zhǎng)型發(fā)展，對(duì)應(yīng)的最大航程也越來(lái)越大，這說(shuō)明細(xì)長(zhǎng)型外形具有更好的氣動(dòng)性能，是綜合考慮外形和軌跡的優(yōu)化設(shè)計(jì).

References)

［1］ Nan Ying，Chen Shilun，Yan Hui.A common numerical calcula-tion method of optimizing the trajectories of space vehicles［J］.Flight Dynamics，1996，9:20 －26

［2］ Benson D.A Gauss pseudospectral transcription for optimal control［D］.Boston:Massachusetts Institute of Technology，2004

［3］ Huntington G T.Advancement and analysis of a Gauss pseudospectral transcription for optimal control problems［D］.Boston:Massachusetts Institute of Technology，2007

［4］ Yan Hui，Chen Shilu，Nan Ying.Static and dynamic hybrid optimization［J］.AIAA，1997:231 －233

［5］ Hull D G.Optimal control theory for applications［M］.Berlin:Springer-Verlag，2003

［6］ Zhu Xiaolin.Numerical analysis［M］.Heifei:University of Science and Technology of China Press，2010:255 －272

［7］ Shampine L F，Reichelt MW，Kierzenka J.Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c［EB/OL］.http://www.mathworks.com/bvp_tutorial

［8］ Nonweiler T R.Aerodynamic problems of manned space vehicles［J］.Journal of the Royal Aeronautical Society，1959，63(2):521－528

［9］趙志.乘波構(gòu)型前體的設(shè)計(jì)與性能計(jì)算［D］.西安:西北工業(yè)大學(xué)，2006 Zhao Zhi.Design and performance calculation of waverider fore body［D］.Xi’an:Northwestern Polytechnical University，2006(in Chinese)

［10］王爍，李萍，陳萬(wàn)春.錐導(dǎo)乘波體氣動(dòng)代理建模方法研究［J］.飛行力學(xué)，2012(1):43 －47 Wang Shuo，Li Ping，Chen Wanchun.Reserch on the surrogate of model aerodynamic performance of cone derived waverider［J］.Flight Dynamics，2012(1):43 － 47(in Chinese)

［11］高建力.高超聲速飛行器氣動(dòng)特性估算與分析［D］.西安:西北工業(yè)大學(xué)，2007 Gao Jianli.Estimating and analyzing of aerodynamic of hypersonic vehicle［D］.Xi’an:Northwestern Polytechnical University，2007(in Chinese)

［12］王振國(guó)，陳小前，羅文彩，等.飛行器多學(xué)科設(shè)計(jì)優(yōu)化理論與應(yīng)用研究［M］.北京:國(guó)防工業(yè)出版社，2006 Wang Zhenguo，Chen Xiaoqian，Luo Wencai.Research on the theory and application of multidisciplinary design optimization of flight vehicles［M］.Beijing:National Defense Industry Press，2006(in Chinese)