基于小波去噪和隨機(jī)子空間算法的廣域低頻振蕩估計(jì)

，，，

(四川大學(xué)電氣信息學(xué)院，四川 成都 610065)

0 引 言

隨著大型機(jī)組快速勵(lì)磁系統(tǒng)的采用以及電力系統(tǒng)規(guī)模的不斷擴(kuò)大、互聯(lián)，低頻振蕩問(wèn)題日益突出，嚴(yán)重威脅著電力系統(tǒng)的安全穩(wěn)定運(yùn)行。按照振蕩的頻率和涉及的范圍，低頻振蕩通常劃分為兩種形式：局部模式和廣域模式[1-2]。 其中，廣域模式為區(qū)域間振蕩，即系統(tǒng)中某區(qū)域機(jī)群與另一區(qū)域機(jī)群的相對(duì)振蕩。相對(duì)于局部模式，該模式的成因、影響因素和控制都更為復(fù)雜，且對(duì)系統(tǒng)穩(wěn)定的破壞程度大，因而更值得運(yùn)行人員關(guān)注。近年來(lái)，隨著相量測(cè)量裝置(phasor measurement unit，PMU)的徹底實(shí)用化以及基于PMU的廣域相量測(cè)量系統(tǒng)(WAMS)的逐步建成并在電力系統(tǒng)中應(yīng)用，使得利用在線的廣域向量測(cè)量數(shù)據(jù)進(jìn)行廣域低頻振蕩分析成為可能[3]。目前通過(guò)分析實(shí)測(cè)數(shù)據(jù)識(shí)別和分析低頻振蕩模式的方法有Prony 算法[4]、自回歸滑動(dòng)平均(auto-regressive and moving average，ARMA)算 法[5]和希爾伯特-黃變換 (Hilbert-Huang transform，HHT)[6]等先進(jìn)的數(shù)學(xué)方法，通過(guò)對(duì)某一局部動(dòng)態(tài)觀測(cè)信息的信號(hào)處理，分析系統(tǒng)的低頻振蕩現(xiàn)象。但上述方法存在受噪聲信號(hào)影響較大，系統(tǒng)階數(shù)確定困難，容易出現(xiàn)偽模態(tài)和計(jì)算過(guò)程復(fù)雜、耗時(shí)長(zhǎng)等缺點(diǎn)。

隨機(jī)子空間辨識(shí)(stochastic subspace identification，SSI)算法能夠從實(shí)測(cè)振蕩信號(hào)中提取振蕩頻率及阻尼比的同時(shí)還能夠獲得相應(yīng)的振型信息，文獻(xiàn)[7-8]對(duì)隨機(jī)子空間辨識(shí)方法在電力系統(tǒng)低頻振蕩分析中的應(yīng)用做了初步的探索。但建立在線性系統(tǒng)理論以及所受擾動(dòng)為平穩(wěn)信號(hào)假設(shè)的基礎(chǔ)上的隨機(jī)子空間辨識(shí)方法在處理非線性、非平穩(wěn)的電力系統(tǒng)實(shí)測(cè)振蕩信號(hào)方面的有效性和準(zhǔn)確性有待研究和驗(yàn)證。鑒于小波分析[9]能以不同的小波變換尺度,將信號(hào)分解成不同的頻段分量,具有良好的時(shí)、頻局域性,在處理非平穩(wěn)信號(hào)時(shí)具有良好的效果，因此，結(jié)合小波去噪和隨機(jī)子空間辨識(shí)算法，開(kāi)展電力系統(tǒng)低頻振蕩在線分析的研究。

1 小波去噪

在小波變換應(yīng)用中,目前主要有硬閾值和軟閾值去噪方法[10]。由于噪聲信號(hào)強(qiáng)度的隨機(jī)性,以及小波分解過(guò)程中信號(hào)與噪聲的傳播特性不同,每一層小波分解系數(shù)所采用的閾值應(yīng)該是隨小波系數(shù)的變化而變化的，能實(shí)現(xiàn)這種變動(dòng)閾值的方法就是軟閾值去噪方法，而硬閾值算法[11]由于其自身缺陷而不適用于實(shí)際場(chǎng)合。軟閾值去噪方法近年來(lái)得到很大發(fā)展,其去噪效果被證明是很有效的。

1.1 小波軟閾值消噪原理

含有噪聲的一維信號(hào)可以表示成如下形式。

s(i)=f(i)+u(i)

(1)

其中,f(i)為真實(shí)信號(hào);u(i)為高斯白噪聲;s(i)為含噪聲的信號(hào)。對(duì)信號(hào)s(i)進(jìn)行消噪的目的就是要抑制信號(hào)中的噪聲部分,從而在s(i)中恢復(fù)出真實(shí)信號(hào)f(i)。在實(shí)際工程中,有用信號(hào)通常表現(xiàn)為低頻信號(hào)或是一些比較平穩(wěn)的信號(hào),而噪聲信號(hào)則通常表現(xiàn)為高頻信號(hào)。一般來(lái)說(shuō),一維信號(hào)的消噪算法可以分為3個(gè)步驟進(jìn)行：①對(duì)信號(hào)進(jìn)行小波分解;②小波分解高頻系數(shù)的閾值量化;③對(duì)信號(hào)進(jìn)行重構(gòu)。

在這3個(gè)步驟中,最關(guān)鍵的一步就是如何選取閾值方式和如何進(jìn)行閾值的量化,從某種程度上來(lái)說(shuō),它直接關(guān)系到信號(hào)消噪的質(zhì)量。

1.2 軟閾值的選取

軟閾值的選取方法很多[12]。經(jīng)比較,下面采用啟發(fā)式閾值(heursure)方法,它是在通用閾值和無(wú)偏風(fēng)險(xiǎn)閾值的基礎(chǔ)上進(jìn)行計(jì)算的，這種方法閾值風(fēng)險(xiǎn)較小，有用信號(hào)不易丟失。具體計(jì)算原理和計(jì)算步驟如下[13]。

(1)噪聲強(qiáng)度的計(jì)算

噪聲強(qiáng)度的計(jì)算可采用以下公式。

(2)

(2)通用閾值的計(jì)算

通用閾值計(jì)算的理論依據(jù)是:N個(gè)具有獨(dú)立同分布的標(biāo)準(zhǔn)高斯變量中的最大值小于T1的概率隨著N的增大而趨于1。其中,T1由式(3)來(lái)計(jì)算。

(3)

式中，σ為噪聲強(qiáng)度;N為所處理的變量的個(gè)數(shù)。

(3) Stein無(wú)偏風(fēng)險(xiǎn)閾值的計(jì)算

將某一層小波系數(shù)的平方按由小到大排列,得到一個(gè)向量:W=[w1,w2,…,wN],其中,w1≤w2≤…≤wN，N為小波系數(shù)的個(gè)數(shù)。由此計(jì)算風(fēng)險(xiǎn)向量R=[r1,r2,…,rN],其中

(4)

以R元素中的最小值rb作為風(fēng)險(xiǎn)值,由rb的下標(biāo)變量b求出對(duì)應(yīng)的wb,則閾值T2為

(5)

(4)啟發(fā)式閾值的計(jì)算

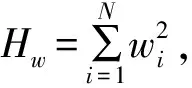
(6)

最終的軟閾值就是T3。

1.3 非平穩(wěn)信號(hào)的小波軟閾值去噪

在實(shí)際的工程應(yīng)用中，大多數(shù)信號(hào)可能包含著許多尖峰或突變，而且噪聲信號(hào)也并不是平穩(wěn)的白噪聲。對(duì)這種信號(hào)進(jìn)行去噪處理時(shí)，傳統(tǒng)的傅里葉變換完全是在頻域中對(duì)信號(hào)進(jìn)行分析，它不能給出信號(hào)在某個(gè)時(shí)間點(diǎn)上的變化情況，因此分辨不出信號(hào)在時(shí)間軸上的一個(gè)突變。但是小波分析能同時(shí)在時(shí)頻域內(nèi)對(duì)信號(hào)進(jìn)行分析，所以它能有效地區(qū)分信號(hào)中的突變部分和噪聲，從而實(shí)現(xiàn)對(duì)非平穩(wěn)信號(hào)的去噪。如圖1所示，使用小波軟閾值去噪方法對(duì)一個(gè)含噪的矩形波信號(hào)進(jìn)行去噪處理，說(shuō)明此方法對(duì)非平穩(wěn)信號(hào)具有良好的去噪效果。

2 隨機(jī)子空間理論

2.1 隨機(jī)子空間思想

隨機(jī)子空間辨識(shí)[14]方法是近年來(lái)發(fā)展的一種線性系統(tǒng)辨識(shí)方法，可以有效地從環(huán)境激勵(lì)的系統(tǒng)響應(yīng)中獲取模態(tài)參數(shù)。它采用簡(jiǎn)單可靠的數(shù)學(xué)工具如矩陣的正交三角分解QR(QR factorization)和奇異值分解SVD(singular value decomposition)獲取狀態(tài)矩陣及其特征值，結(jié)合最小二乘法，得到信號(hào)的振蕩參數(shù)。

圖1 含噪矩形波的去噪結(jié)果

在實(shí)際應(yīng)用中，量測(cè)數(shù)據(jù)在時(shí)間上都是離散的，所以經(jīng)離散采樣后，可得如下隨機(jī)狀態(tài)空間系統(tǒng)。

(7)

式中，A為系統(tǒng)矩陣；C為輸出矩陣；wk、vk分別為零均值過(guò)程噪聲和測(cè)量噪聲，且互不相關(guān)。根據(jù)輸出數(shù)據(jù)yk可構(gòu)造 Hankel矩陣Y0/2i-1，如式(8)。

(8)

其中，下標(biāo)0/2i-1表示 Hankel 矩陣第一列的第一塊行和最后一塊行的下標(biāo)，下標(biāo)p和f分別表示“過(guò)去”和“將來(lái)”。

定義輸出yk自協(xié)方差矩陣Ri為

(9)

由協(xié)方差序列組成的Toeplize矩陣T1/i為

(10)

對(duì)Toeplize矩陣進(jìn)行奇異值分解，秩為非零的奇異值個(gè)數(shù)，亦為系統(tǒng)的階數(shù)。

(11)

Tl/i可分解為Tl/i=ОiГi，其中，Оi為可觀矩陣；Гi為反轉(zhuǎn)隨機(jī)可控矩陣。根據(jù)上式可得如下系統(tǒng)矩陣A和C。

(12)

C=Oi(1∶l)

(13)

2.2 模態(tài)識(shí)別

得到系統(tǒng)狀態(tài)矩陣A后，對(duì)其進(jìn)行特征值分解：Ψ-1ΛΨ=A,獲得系統(tǒng)的特征值λi(i=1,2,…,n)，設(shè)采樣時(shí)間間隔Δt，則信號(hào)的頻率fi和阻尼比ξi以及振型Ф為

fi=argλi/(2πΔt)

(14)

αi=1n|λi|/Δt

(15)

(16)

Φ=Cψ

(17)

綜上所述，隨機(jī)子空間算法根據(jù)系統(tǒng)的輸出數(shù)據(jù)，可以識(shí)別出電力系統(tǒng)線性化模型{A，C}，進(jìn)一步即可識(shí)別全部振蕩參數(shù)。

2.3 隨機(jī)子空間算法的有效性分析

按下式產(chǎn)生一理想信號(hào)。

x=160.74e-0.15tcos(2π×0.46t+1.32)

+173.38e-0.452tcos(2π×1.53t+0.86)

(18)

此信號(hào)包含兩個(gè)振蕩模式。在此信號(hào)上疊加一個(gè)噪聲強(qiáng)度為2 dBM的高斯白噪聲作為測(cè)試信號(hào)來(lái)驗(yàn)證算法的有效性。信號(hào)的時(shí)間長(zhǎng)度為(0～10)s,采樣頻率為20 Hz(采樣間隔0.05 s)。經(jīng)奇異值分解計(jì)算可知隨機(jī)子空間辨識(shí)過(guò)程的階數(shù)應(yīng)定為4階，然后得到系統(tǒng)狀態(tài)矩陣A。

(19)

最終辨識(shí)結(jié)果與理論值的比較見(jiàn)表1。

通過(guò)比較發(fā)現(xiàn)，此方法能較準(zhǔn)確地辨識(shí)出信號(hào)各模式的頻率、阻尼比，具有很高的頻率分辨率。

表1 隨機(jī)子空間法辨識(shí)結(jié)果與理論值比較

3 仿真實(shí)例

算例采用IEEE 16機(jī)68 節(jié)點(diǎn)系統(tǒng)[14]如圖2所示。系統(tǒng)可劃分為5個(gè)區(qū)域：Group 1，新英格蘭(G1～G9)；Group 2，紐約(G10～G13)；Group 3， 等效機(jī)組G14；Group 4，等效電機(jī) G15；Group 5，等效電機(jī) G16。系統(tǒng)中存在著 3 個(gè)弱阻尼的互聯(lián)振蕩模式，分別為 0.37、0.5、0.61 Hz。表2給出了傳統(tǒng)小干擾特征根的分析結(jié)果。

圖2 16機(jī)68節(jié)點(diǎn)系統(tǒng)圖

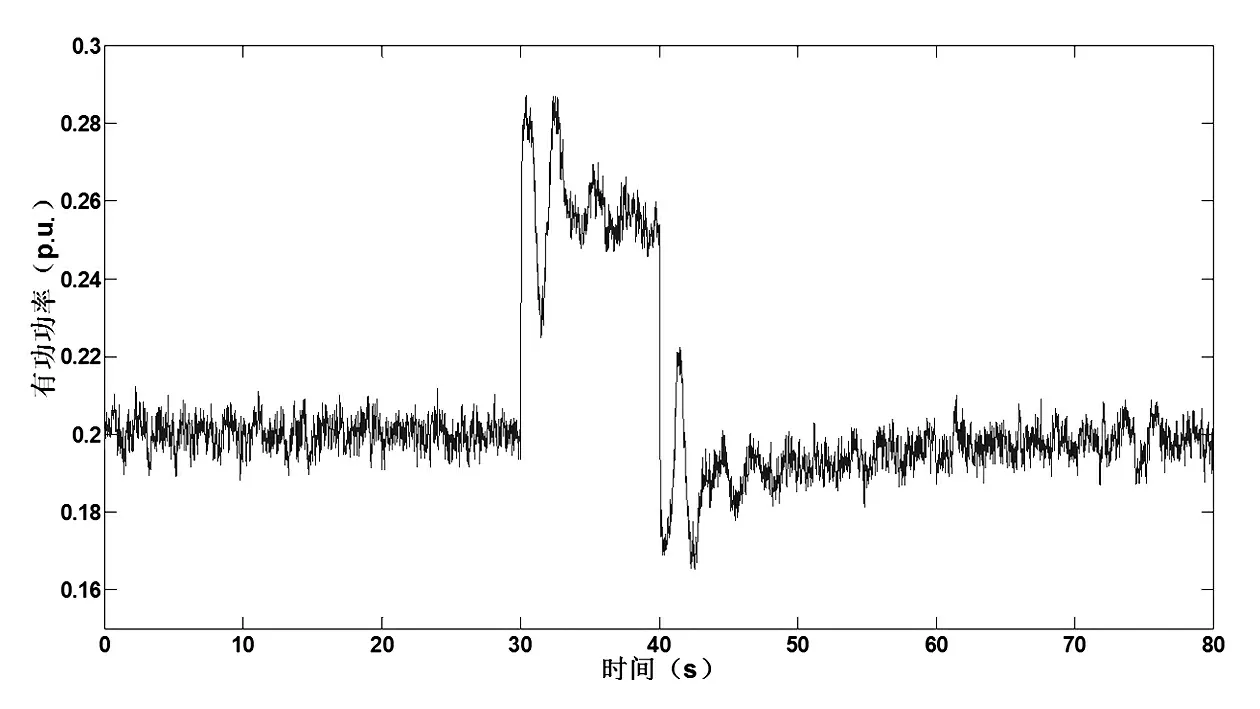
圖3 聯(lián)絡(luò)線上有功波動(dòng)

在系統(tǒng)正常運(yùn)行方式下，模擬在母線9 上增加隨機(jī)負(fù)荷，t=30 s時(shí)增加一個(gè)0.1 p.u.的階躍負(fù)荷，t=40 s時(shí)去除階躍負(fù)荷，以形成非平穩(wěn)信號(hào)。記錄聯(lián)絡(luò)線8～9上傳送的有功功率，采樣間隔為 0.1 s，分析0～100 s間數(shù)據(jù)，其波形見(jiàn)圖3。

圖4 去噪后有功波動(dòng)

應(yīng)用小波啟發(fā)式軟閾值方法對(duì)采樣數(shù)據(jù)進(jìn)行去噪處理(見(jiàn)圖4)，然后用隨機(jī)子空間法辨識(shí)振蕩的主導(dǎo)模式，并與未采用小波去噪的分析結(jié)果對(duì)比，結(jié)果見(jiàn)表3。圖5給出了辨識(shí)得到的3 個(gè)模式的模態(tài)圖(橫坐標(biāo)為發(fā)電機(jī)號(hào)，縱坐標(biāo)為幅值)，從圖中可以看出頻率為0.384 6的互聯(lián)振蕩模式的參與機(jī)組有Group 1～Group 5,頻率為0.511 2的互聯(lián)振蕩模式的主要參與機(jī)組有Group 3、Group 5，頻率為0.648 5的互聯(lián)振蕩模式的主要參與機(jī)組有Group 1、Group 2。

圖5 模態(tài)圖

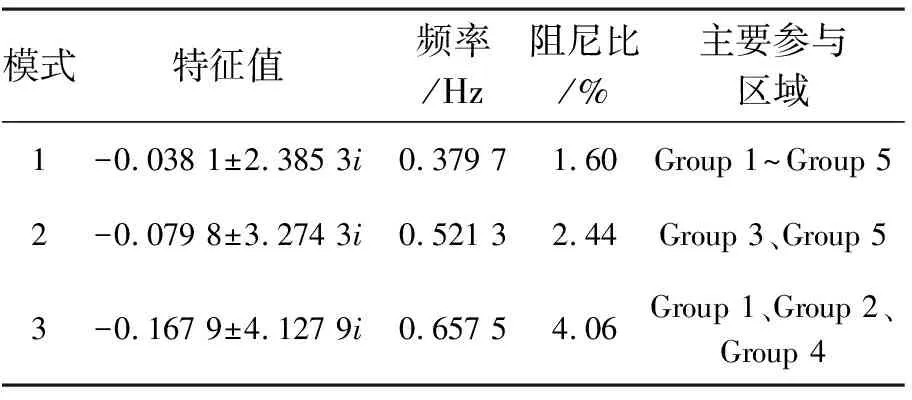
模式特征值頻率/Hz阻尼比/%主要參與區(qū)域1-0.038 1±2.385 3i0.379 71.60Group 1～Group 52-0.079 8±3.274 3i0.521 32.44Group 3、Group 53-0.167 9±4.127 9i0.657 54.06Group 1、Group 2、Group 4

由表3可以看出，聯(lián)絡(luò)線上的有功發(fā)生了頻率分別為 0.384 6 Hz、0.511 2 Hz、0.648 5 Hz的低頻振蕩，為區(qū)間振蕩模式，印證了隨機(jī)子空間法的正確性，而且小波去噪的去噪處理起到了較好的效果，此方法在處理非平穩(wěn)信號(hào)時(shí)具有很大優(yōu)勢(shì)，較適合對(duì)實(shí)際大電網(wǎng)的實(shí)測(cè)信號(hào)的分析。

表3 去噪后分析結(jié)果與未去噪分析結(jié)果及理論值比較

4 結(jié) 論

提出了一種利用小波去噪技術(shù)對(duì)振蕩數(shù)據(jù)進(jìn)行預(yù)處理, 然后運(yùn)用隨機(jī)子空間方法對(duì)數(shù)據(jù)進(jìn)行分析的新方法, 用于電力系統(tǒng)低頻振蕩信號(hào)特征的提取，特別是對(duì)非平穩(wěn)信號(hào)的處理具有有效性和準(zhǔn)確性。而且隨機(jī)子空間方法具有參數(shù)少、抗噪能力較強(qiáng)、分辨率較高、擬合效果較好等優(yōu)點(diǎn), 滿足低頻振蕩辨識(shí)和系統(tǒng)振蕩分析的需要。小波預(yù)處理技術(shù)在提高精確度的同時(shí), 也降低了分析速度。

[1] Klein M，Rogers G J，Kunder P．A Fundamental Study of Inter-area oscillations in Power Systems[J]．Power Systems，1991，6(3)：914-921．

[2] Task Force of Advisory Group 01 of Study Committee 38．GIGRE Technical Brochure on Analysis and Control on Power System Oscillation[R]．Paris：GIGRE Special Publication，1996．

[3] 鞠平，謝歡，孟遠(yuǎn)景,等.基于廣域測(cè)量信息在線辨識(shí)低頻振蕩[J].中國(guó)電機(jī)工程學(xué)報(bào)，2005，22(10)：59-63.

[4] 竺煒，唐穎杰，周有慶，等．基于改進(jìn) Prony 算法的電力系統(tǒng)低頻振蕩模式識(shí)別[J]．電網(wǎng)技術(shù)，2009，33(5)：44-47．

[5] Wies R W，Pierre J W，Trudnowski D J．Use of ARMA Block Processing for Estimating Stationary Low-frequency Electromechanical Modes of Power Systems[J]．IEEE Trans on Power Systems.2003，18(1)：167-173．

[6] 韓松，何利銓，孫斌，等．基于希爾伯特-黃變換的電力系統(tǒng)低頻振蕩的非線性非平穩(wěn)分析及其應(yīng)用[J]．電網(wǎng)技術(shù)，2008，32(4)：56-60．

[7] Ghasemi H，Canizares C，Moshref A．Oscillatory Stability Limit Prediction Using Stochastic Subspace Identification[J]．IEEE Trans.on Power Systems，2006，21(2)：736-745.

[8] 陳卓．工況模態(tài)分析在低頻振蕩辨識(shí)中的應(yīng)用初探[J]．電力系統(tǒng)保護(hù)與控制，2009，37(8)：34-37．

[9] Mallat S,Hwang W L. Singularity Detection and Processing with Wavelets[J].IEEE Trans on Information Theory,1992,38(2): 617-643.

[10] D. L. Donoho. De-noising by Soft- thresholding[J].IEEE Transactions on Information Theory, 1995, 41(3): 613-627.

[11] Santoso S, Powers E J, Grady W M. Power Quality Disturbance Data Compression Using Wavelet Transform Methods[J].IEEE Trans on Power Delivery,1997,12(3): 1250-1257.

[12] Carl T. The What, How, and Why of Wavelet Shrinkage Denoising[J].Computing in Science & Engineering, 2000, 2(3):12-19.

[13] Hilton L, Ogden T. Data Analytic Wavelet Threshold Selection in 2-D Signal Denoising[J].IEEE Trans on Signal Processing,1997,45(2): 496-500.

[14] Van Overschee Peter，De Moor Bart． Subspace Algorithms for the Stochastic Identification Problem[C]∥The IEEE Conference on Decision and Control，Brighton，England: 1991．