格值直覺模糊有限自動機的直積與覆蓋

楊 莉, 莫智文

(四川師范大學 數學與軟件科學學院, 四川 成都 610066)

1965年,L. A. Zadeh[1]提出模糊集理論.隨后,在1967年W. G. Wee[2]引入了模糊自動機理論.J. N. Mordeson[3]等對模糊自動機的代數性質做了詳細的研究.隨著模糊集理論的發展，1983年K. T. Atanassov[4]提出了直覺模糊集，它是一種高層次的模糊集，比一般的模糊集合多了一個非隸屬度，這就使得它在處理不確定信息時比傳統的模糊集有更強的靈活性和準確性,K. T. Atanassov等[5]又在1984年提出了格值直覺模糊集，格值直覺模糊集理論是直覺模糊集理論的推廣.Y. B. Jun[6]于2005年提出了直覺模糊有限自動機的概念,不久Y. B. Jun[7-8]和X. W. Zhang等[9]對直覺模糊有限自動機的代數性質做了詳細研究.在此基礎上，提出了格值直覺模糊有限自動機的定義，當L=[0,1]時，格值直覺模糊有限自動機就為直覺模糊有限自動機，因此格值直覺模糊有限自動機是直覺模糊有限自動機的推廣.自動機的乘積在分解和覆蓋定理中起著很重要的作用，因此對自動機乘積的研究是必要的.文獻[10-15]建立了自動機的乘積理論.基于此，本文建立了格值直覺模糊有限自動機的直積理論，并得到了一些重要性質.

1 預備知識

特別地，完備格L一定有一最小元和最大元，即infL和supL，分別記為0和1.

定理1.1[17]在任意格L中，下述2個分配恒等式等價：

(D1)a∧(b∨c)=(a∧b)∨(a∧c),?a,b,c∈L;

(D2)a∨(b∧c)=(a∨b)∧(a∨c),?a,b,c∈L.

滿足分配恒等式D1(或D2)的格L叫做一個分配格.

定理1.2[17]在任意格(L,≤)中，對?a,b,c∈L有

(L1)a∧a=a,a∨a=a;(冪等律)

(L2)a∧b≤b∧a,a∨b≤b∨a;(交換律)

(L3)a∧(b∧c)≤(a∧b)∧c,a∨(b∨c)≤(a∨b)∨c;(結合律)

(L4)a∧(a∨b)=a=a∨(a∧b).(吸收律)

定理1.3[17]在任意格L中,交、并運算是保序的，即對?a,b,c∈L，若a≤b，則a∧c≤b∧c,a∨c≤b∨c.

定義1.2[18]′:L→L是格L上的逆序對合對應，即對任意的a,b∈L，a≤b時有a′≥b′且a″=a.

若0,1分別是完備格L的最小元與最大元，則0′=1,1′=0.

定理1.4[18]設L是具有逆序對合對應的完備格，則De Morgan對偶律成立,即對{ai|i∈I}?L有

定義1.3[5]設X是一個非空集合，L是具有逆序對合對應的完備格，X上的一個格值直覺模糊集A定義為

A={〈x,μA(x),νA(x)〉|x∈X},

其中μA:X→L,νA:X→L，分別表示X上的元素x屬于A的隸屬度和非隸屬度，′:L→L且對?x∈X，滿足

μA(x)≤(νA(x))′.

格值直覺模糊集A可以簡記為A=(μA,νA).

2 格值直覺模糊有限自動機

定義2.1一個格值直覺模糊有限自動機(簡寫為LIFFSM)是三元組M=(Q,X,A)，其中

1)Q表示非空有限狀態集合;

2)X表示非空有限輸入符號集合;

3)A=(μA,νA)表示一個Q×X×Q上的格值直覺模糊集，即μA:X→L,νA:X→L,′:L→L且對?x∈X，滿足μA(x)≤(νA(x))′,A叫做格值直覺模糊轉移函數.

當L=[0,1]時，格值直覺模糊有限自動機M就為直覺模糊有限自動機，因此格值直覺模糊有限自動機是直覺模糊有限自動機的推廣.

令X*表示X上所有有窮長度的串的集合，令Λ表示X*上的空串，對于任意的x∈X*,|x|表示x的長度.

定義2.2若M=(Q,X,A)是格值直覺模糊有限自動機，定義一個Q×X*×Q上的格值直覺模糊集A*=(μA*,νA*)為：對?q,p∈Q，x∈X*,a∈X,

定理2.1設M=(Q,X,A)為格值直覺模糊有限自動機，則

μA=μA*|Q×X×Q,νA=νA*|Q×X×Q.

定理2.2下列條件相互等價：

1) (L,∨,∧)是分配格，即滿足分配恒等式D1(或D2)；

2) 設M=(Q,X,A)為任意格值直覺模糊有限自動機，?q,p∈Q，x,y∈X*有

3) 設M=(Q,X,A)為任意格值直覺模糊有限自動機，則?q,p∈Q,x=x1x2…xn∈X*,xi∈X,i=1,2,…,n,有

μA(r1,x2,r2)∧…∧μA(rn-1,xn,p)],

νA(r1,x2,r2)∨…∨νA(rn-1,xn,p)].

證明1)?2) 根據y的長度，用數學歸納法證明.

2)?1) 取M=(Q,X,A)如下：Q={q0,q1,q2,q3,q4},X={x1,x2,x3},μA(q0,x1,q1)=a,μA(q1,x2,q2)=μA(q1,x2,q3)=1,μA(q2,x3,q4)=b,μA(q3,x3,q4)=c,其余情況取μA(qi,xj,qk)=0.νA(q0,x1,q1)=d,νA(q1,x2,q2)=νA(q1,x2,q3)=0,νA(q2,x3,q4)=e,νA(q3,x3,q4)=f,其余情況取νA(qi,xj,qk)=1.滿足a≤d′,b≤e′,c≤f′.

令x=x1,y=x2x3,則有

μA*(q0,xy,q4)=μA*(q0,x1x2x3,q4)=

μA(q0,x1,q1)∧μA*(q1,x2x3,q4),

μA*(q1,x2x3,q4)=

(1∧b)∨(1∧c)=b∨c,

又μA(q0,x1,q1)=a，從而有

μA*(q0,xy,q4)=a∧(b∨c).

又因為

μA*(q0,xy,q4)=μA*(q0,x1x2x3,q4)=

[μA*(q0,x1x2,q2)∧μA(q2,x3,q4)]∨

[μA*(q0,x1x2,q3)∧μA(q3,x3,q4)]=

[μA*(q0,x1x2,q2)∧b]∨

[μA*(q0,x1x2,q3)∧c],

μA*(q0,x1x2,q2)=

μA(q0,x1,q1)∧μA*(q0,x1x2,q3)=

μA(q0,x1,q1)∧μA(q1,x2,q3)=a∧1=a,

從而有

μA*(q0,xy,q4)=(a∧b)∨(a∧c),

則

a∧(b∨c)=(a∧b)∨(a∧c).

即滿足分配恒等式D1，則(L,∨,∧)是分配格.

同理可以證明1)?3)和3)?1).

3 格值直覺模糊有限自動機的直積

定義3.1設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2.稱M1×M2=(Q1×Q2,X1×X2,A1×A2)為M1與M2的全直積.其中μA1×A2:(Q1×Q2)×(X1×X2)×(Q1×Q2)→L,νA1×A2:(Q1×Q2)×(X1×X2)×(Q1×Q2)→L,?(q1,q2),(p1,p2)∈Q1×Q2,?(x1,x2)∈X1×X2，有

μA1×A2((q1,q2),(x1,x2),(p1,p2))=

μA1(q1,x1,p1)∧μA2(q2,x2,p2),

νA1×A2((q1,q2),(x1,x2),(p1,p2))=

νA1(q1,x1,p1)∨νA2(q2,x2,p2).

由定義3.1當X1=X2=X時，可以定義格值直覺模糊有限自動機的限制直積，其定義如下：

定義3.2設Mi=(Qi,X,Ai)是格值直覺模糊有限自動機，i=1,2.稱M1∧M2=(Q1×Q2,X,A1∧A2)為M1與M2的限制直積,其中μA1∧A2:(Q1×Q2)×X×(Q1×Q2)→L,νA1∧A2:(Q1×Q2)×X×(Q1×Q2)→L,?(q1,q2),(p1,p2)∈Q1×Q2,a∈X，有

μA1∧A2((q1,q2),a,(p1,p2))=

μA1(q1,a,p1)∧μA2(q2,a,p2),

νA1∧A2((q1,q2),a,(p1,p2))=

νA1(q1,a,p1)∨νA2(q2,a,p2).

定理3.1設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2,則有

1)M1×M2是格值直覺模糊有限自動機;

2)M1∧M2是格值直覺模糊有限自動機,其中X1=X2=X.

證明1) 要證全直積M1×M2為格值直覺模糊有限自動機，只需證A1×A2為格值直覺模糊集.?(q1,q2),(p1,p2)∈Q1×Q2,?(x1,x2)∈X1×X2有

μA1×A2((q1,q2),(x1,x2),(p1,p2))=

μA1(q1,x1,p1)∧μA2(q2,x2,p2),

νA1×A2((q1,q2),(x1,x2),(p1,p2))=

νA1(q1,x1,p1)∨νA2(q2,x2,p2),

則

(νA1×A2((q1,q2),(x1,x2),(p1,p2)))′=

(νA1(q1,x1,p1)∨νA2(q2,x2,p2))′=

(νA1(q1,x1,p1))′∧(νA2(q2,x2,p2))′.

因為A1,A2為格值直覺模糊集，所以

μA1(q1,x1,p1)≤(νA1(q1,x1,p1))′,

μA2(q2,x2,p2)≤(νA2(q2,x2,p2))′.

根據任意格L中,交、并運算是保序的，則

μA1(q1,x1,p1)∧μA2(q2,x2,p2)≤

(νA1(q1,x1,p1))′∧(νA2(q2,x2,p2))′,

即

μA1×A2((q1,q2),(x1,x2),(p1,p2))≤

(νA1×A2((q1,q2),(x1,x2),(p1,p2)))′.

所以A1×A2為格值直覺模糊集，則M1與M2的格值直覺直積M1×M2為格值直覺模糊有限自動機.

類似地可證明2).

性質3.1若L為分配格，Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2.M1×M2為M1與M2的全直積,則對?(q1,q2),(p1,p2)∈Q1×Q2,?(x,y)∈(X1×X2)*有

μ(A1×A2)*((q1,q2),(x,y),(p1,p2))=

ν(A1×A2)*((q1,q2),(x,y),(p1,p2))=

證明1) 當|x|=|y|=0時，即x=y=Λ時，

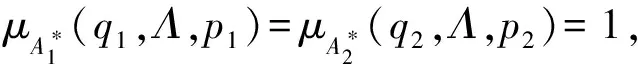
μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

綜上|x|=|y|=0時有

μ(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

同理可證

ν(A1×A2)*((q1,q2),(Λ,Λ),(p1,p2))=

因此，|x|=|y|=0時，結論成立.

2) 若|x|=|y|=n-1(n>0)時，結論成立.

3) ?(a,b)∈X1×X2,則(xa,yb)∈(X1×X2)*，且|xa|=|yb|=n，則

μ(A1×A2)*((q1,q2),(xa,yb),(p1,p2))=

μ(A1×A2)*((q1,q2),(x,y)(a,b),(p1,p2))=

即|x|=|y|=n時，

μ(A1×A2)*((q1,q2),(x,y),(p1,p2))=

同理可證

ν(A1×A2)*((q1,q2),(x,y),(p1,p2))=

綜上所述，結論成立.

性質3.2若L為分配格，Mi=(Qi,X,Ai)是格值直覺模糊有限自動機，i=1,2.M1∧M2為M1與M2的限制直積,則?(q1,q2),(p1,p2)∈Q1×Q2,?x∈X*有

μ(A1∧A2)*((q1,q2),x,(p1,p2))=

ν(A1∧A2)*((q1,q2),x,(p1,p2))=

證明利用|x|的長度用數學歸納法證明,方法類似于性質3.1的證明.

4 格值直覺模糊有限自動機的直積之間的覆蓋關系

定義4.1設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2.如果η:Q2→Q1是一滿的部分函數，ξ:X1→X2是一函數，則稱序對(η,ξ)是M2對M1的覆蓋，記作M1≤M2，如果滿足對?x1∈X1,p,q∈domain(η)有

μA1(η(p),x1,η(q))≤μA2(p,ξ(x1),q),

νA1(η(p),x1,η(q))≥νA2(p,ξ(x1),q).

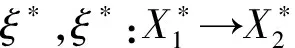
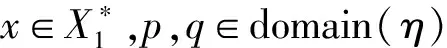
證明根據x的長度，用數學歸納法證明.

1) 當|x|=1時結論顯然成立;

2) 假設|x|=n-1時結論成立;

3) 若|x|=n,x=x1x2…xn-1xn,?xi∈X1則

μA1(r1,xn,η(q))]=

μA1(η(p2),xn,η(q))|η(p2)=r1}≤

μA1(p2,ξ(xn),q)]=

定理4.1設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2,3.若M1≤M2,M2≤M3,則M1≤M3.

證明因為M1≤M2,所以存在滿的部分函數η1:Q2→Q1,函數ξ1:X1→X2,對?x1∈X1,p2,q2∈domain(η1)有

μA1(η1(p2),x1,η1(q2))≤μA2(p2,ξ1(x1),q2),

νA1(η1(p2),x1,η1(q2))≥νA2(p2,ξ1(x1),q2).

又因為M2≤M3,所以存在滿的部分函數η2:Q3→Q2,函數ξ2:X2→X3,對?x2∈X2,p3,q3∈domain(η2)有

μA2(η2(p3),x2,η2(q3))≤μA3(p3,ξ(x2),q3),

νA2(η2(p3),x2,η2(q3))≥νA3(p3,ξ(x2),q3).

令η=η1°η2:Q3→Q1,ξ=ξ2°ξ1:X1→X3.顯然η是一滿的部分函數,ξ是一函數,并且對對?x1∈X1,p,q∈domain(η)?domain(η2)有

μA1(η(p),x1,η(q))=

μA1(η1°η2(p),x1,η1°η2(q))=

μA1(η1(η2(p)),x1,η1(η2(q)))≤

μA2(η2(p),ξ1(x1),η2(q))≤

μA3(p,ξ2°ξ1(x1),q)=μA3(p,ξ(x1),q).

同理可證νA1(η(p),x1,η(q))≥μA3(p,ξ(x1),q).因此(η,ξ)是M3對M1的覆蓋，即M1≤M3.

定理4.2設Mi=(Qi,X,Ai)是格值直覺模糊有限自動機,i=1,2.則M1∧M2≤M1×M2.

證明定義η:Q1×Q2→Q1×Q2是Q1×Q2上的恒等映射,顯然滿足η是滿的部分函數.定義ξ:X→X×X為，對?a∈X,有ξ(a)=(a,a)，ξ為一函數,并有

μA1∧A2(η((p1,p2)),a,η((q1,q2)))=

μA1∧A2((p1,p2),a,(q1,q2))=

μA1(p1,a,q1)∧μA2(p2,a,q2)=

μA1×A2((p1,p2),(a,a),(q1,q2))=

μA1×A2((p1,p2),ξ(a),(q1,q2)).

同理可得

νA1∧A2(η((p1,p2)),a,η((q1,q2)))=

νA1×A2((p1,p2),ξ(a),(q1,q2)).

則(η,ξ)是M2對M1的覆蓋，即M1∧M2≤M1×M2.

定理4.3設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2,3.若M1≤M2，則

1)M1×M3≤M2×M3,M3×M1≤M3×M2;

2)M1∧M3≤M2∧M3,M3∧M1≤M3∧M2,其中X1=X2=X3=X.

證明因為M1≤M2,所以存在滿的部分函數η1:Q2→Q1,函數ξ1:X1→X2,對?x1∈X1,p2,q2∈domain(η1)有

μA1(η1(p2),x1,η1(q2))≤μA2(p2,ξ1(x1),q2),

νA1(η1(p2),x1,η1(q2))≥νA2(p2,ξ1(x1),q2).

定義η2:Q2×Q3→Q1×Q3為對?p2∈Q2,p3∈Q3有η2((p2,p3))=(η2(p2),p3),易知滿足η2是滿的部分函數.定義ξ2:X1×X3→X2×X3為，對?x1∈X1,x3∈X3有ξ2((x1,x3))=(ξ1(x1),x3)，顯然ξ為一函數.由任意格L中交、并運算是保序的,定義3.1和定義4.1,易知(η2,ξ2)是M2×M3對M1×M3的覆蓋,即M1×M3≤M2×M3.同理可證M3×M1≤M3×M2,進而可證M1∧M3≤M2∧M3,M3∧M1≤M3∧M2.

推論4.1設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2,3.若M1≤M2，則

1)M1∧M3≤M2×M3,其中X1=X3=X;

2)M3∧M1≤M3×M2,其中X1=X3=X.

證明利用定理4.1，定理4.2和定理4.3即可得證.

推論4.2設Mi=(Qi,Xi,Ai)是格值直覺模糊有限自動機，i=1,2,3,4.若M1≤M2，M3≤M4,則

1)M1×M3≤M2×M4;

2)M1∧M3≤M2∧M4,其中X1=X2=X3=X4=X;

3)M1∧M3≤M2×M4,其中X1=X3=X.

證明1)和2)的證明利用定理4.1和定理4.3即可得證.3)的證明利用定理4.1和此推論中的1)得證.

5 結語

本文在格值直覺模糊集的框架下,給出了格值直覺模糊有限自動機的定義.格值直覺模糊有限自動機是直覺模糊有限自動機的推廣.因此對格值直覺模糊有限自動機進行研究是有必要的.自動機的乘積是自動機研究的一個重要方面.本文系統的研究了格值直覺模糊有限自動機在全直積和限制直積下的轉移函數性質、覆蓋關系和覆蓋關系的傳遞性質，為進一步研究格值直覺模糊有限自動機奠定了一定的理論基礎.對格值直覺模糊有限自動的乘積研究還有很多工作可以做，比如，格值直覺模糊有限自動機的級聯積、圈積、同態和弱覆蓋等,這些將是今后工作的主要內容.

[1] Zadeh L A. Fuzzy sets[J]. Information and Control,1965,8(3):338-353.

[2] Wee W G. On generalizations of adaptive algorithm and application of the fuzzy sets concept to pattern classification[D]. West Lafayette:Purdue University,1967.

[3] Mordeson J N, Malik D S. Fuzzy Automata and Languages: Theory and Applications[M]. Boca Raton,London:Chapman & Hall/CRC,2002.

[4] Atanassov K T. Intuitionistic Fuzzy Sets[J]. Fuzzy Sets and Systems,1986,20:87-96.

[5] Atanassov K T, Stoeva S. IntuitionisticL-fuzzy sets[C]// Trappl R. Cybernetics and Systems Research. Amsterdam:North-Holland,1984:539-540.

[6] Jun Y B. Intuitionistic fuzzy finite state machines[J]. J Appl Math Comput,2005,17(1/2):109-120.

[7] Jun Y B. Intuitionistic fuzzy finite switchboard state machines[J]. J Appl Math Comput,2006,20(1/2):315-325.

[8] Jun Y B. Intuitionistic fuzzy transformation semigroups[J]. Information Sciences,2007,177:4977-4986.

[9] Zhang X W, Li Y M. Intuitionistic fuzzy recognizers and intuitionistic fuzzy finite automata[J]. Soft Comput,2009,13:611-616.

[10] 馮文俊,易忠,鄧培民. 狀態機和變換半群積的覆蓋關系[J]. 廣西師范大學學報:自然科學版,2007,25(1):26-29.

[11] 劉軍,莫智文. 格值有限自動機的乘積[J]. 高校應用數學學報,2009,24(1):121-126.

[12] 胡忠剛,鄧培民,易忠. 模糊樹自動機的積與覆蓋[J]. 廣西師范大學學報:自然科學版,2009,27(4):31-35.

[13] Liu J, Mo Z W, Qiu D, et al. Products of Mealy-type fuzzy finite state machines[J]. Fuzzy Sets and Systems,2009,160(16):2401-2415.

[14] 翁福利,舒蘭,王澤文. 直覺模糊有限自動機的乘積[J]. 模糊系統與數學,2012,26(4):84-88.

[15] 柏明強. Fuzzy樹自動機的等價性[J]. 四川師范大學學報:自然科學版,2009,32(1):13-16.

[16] Birkhoff G. Lattice Theory[M]. 3rd Ed. Providence RI:AMS Colloquium Publications,1979.

[17] 胡長流,宋振明. 格論基礎[M]. 開封:河南大學出版社,1990.

[18] 王國俊. 映射與逆映射[J]. 商洛師范專科學校學報,1999,10(4):1-7.