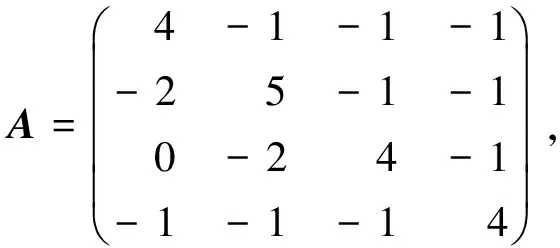M-矩陣與其逆的Hadamard積的最小特征值下界新的估計式
高美平
(文山學院 數學學院, 云南 文山 663000)
許多專家學者對矩陣特征值的估計進行了研究[1-14].因為M-矩陣是一類有重要應用背景的特殊矩陣,所以關于M-矩陣與其逆矩陣的Hadamard積的最小特征值下界的估計式成為被關注的問題之一[1-12].對于M-矩陣A與其逆A-1的Hadamard積最小特征值q(A°A-1)下界問題.M.Fiedler等首先在文獻[1]中得出
(1)
且猜想
(2)
隨后文獻[2-5,9]中證明了M.Fiedler和T.L.Markham的猜想.(2)式形式簡單,計算容易,但矩陣A的階數很大時,該估計式所得的效果不佳.文獻[6]給出了改進的結果,即
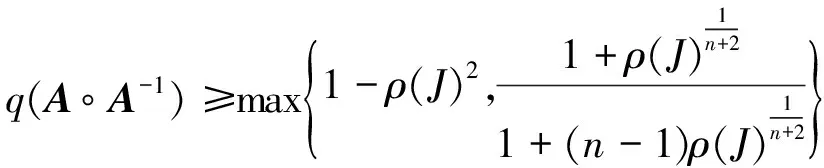
其中ρ(J)是矩陣A的Jacobi迭代矩陣的譜半徑.
當階數n比較大時(3)式改進了(2)式,但由于ρ(J)計算比較復雜,于是文獻[7]從矩陣的元素得出
(4)
其中
H. B. Li等[7]改進了以上結論, Y. Y. Li等在文獻[8]中得出,當A是M-矩陣,A-1是雙隨機矩陣時q(A°A-1)的估計式,即
(5)
文獻[8]還得到M-矩陣A與其逆A-1的Hadamard積的最小特征值下界的估計式
(6)
其中
最近,文獻[12]得到的結果為
(7)
本文繼續對M-矩陣A與其逆A-1的Hadamard積的最小特征值下界問題進行研究,得到了q(A°A-1)新估計式.
1 預備知識
下面先給出一些定義和引理,以便于后面的敘述.
設Cn×n(Rn×n)表示復(實)數域上所有n×n矩陣作成的集合,N表示正整數集.
定義1[15]設
Zn×n=A=(aij)|A∈Rn×n,
aij≤0, ?i,j∈N,i≠j,
則稱An×n的矩陣A為Z矩陣(簡記為A∈Zn×n).
定義2[15]若矩陣A=(aij)∈Rm×n的所有元素aij≥0,則稱矩陣A為非負矩陣,記為A≥0.非負矩陣A=(aij)m×n中的所有元素aij>0,則稱矩陣A為正矩陣,記為A>0.
定義3[15]設A為Z矩陣且A-1≥0,則稱A為(非奇)M-矩陣.
定義4[15]設矩陣A=(aij)m×n,B=(bij)m×n則矩陣A與B的Hadamard積為C=A°B=(cij)m×n,其中cij=aijbij.
定義5[15]矩陣A=(aij)n×n的n個特征值λ1,λ2,…,λn組成的集合稱為A的譜,記為σ(A).
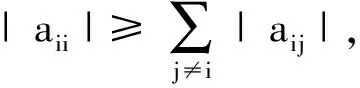
定義7[15]若n階實矩陣A的各行元素之和均為1,則稱A為行隨機矩陣;若n階實矩陣A的各列元素之和均為1,則稱A為列隨機矩陣;若A與AT均為行隨機矩陣,則稱A為雙隨機矩陣.
定義8[16]設矩陣A=(aij)∈Zn×n,記q(A)=min{Re(λ):λ∈σ(A)},稱q(A)為A的最小特征值.
引理1[7](a)若A=(aij)是n階行嚴格對角占優矩陣,則A-1=(bij)滿足
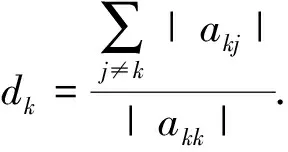
(b) 若A=(aij)是n階列嚴格對角占優矩陣,則A-1=(bij)滿足
j≠i,j∈N,
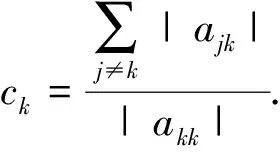
引理2[2]若A是M-矩陣,A-1是雙隨機矩陣,則Ae=e,ATe=e,其中e=(1,…,1)T.
引理3[17]設A=(aij)∈Cn×n,x1,x2,…,xn是任意給定的一組正實數,則A的所有特征值包括在復平面C的如下區域內
引理4[16]設A是非負矩陣,則存在對角元都是正實數的對角矩陣D1和D2使得D1AD2是雙隨機陣.
引理5[1]若P是不可約的M-矩陣且對于非負非零向量z滿足Pz≥kz(其中k∈R),則k≤τ(P).
2 主要結論
2.1逆矩陣元素的估計以下給出嚴格對角占優矩陣A=(aij)的逆矩陣A-1=(bij)的元素bij的估計式.
定理1(a) 若A=(aij)∈Rn×n是行嚴格對角占優矩陣,則A-1=(bij)滿足
(b) 若A=(aij)∈Rn×n是列嚴格對角占優矩陣,則A-1=(bij)滿足
j≠i.
證明(a) 設
因為A是行嚴格對角占優矩陣,所以
因此,存在ε>0使得0 即 j≠i,j∈N. (8) 當j=i時有 (9) 由(8)和(9)式知ARi(ε)是行嚴格對角占優矩陣. 由引理1(a)得 j≠i,j∈N. 也就是 j≠i,j∈N. 上式中令ε→0得 j≠i,j∈N. (b) 設 因為A是列嚴格對角占優矩陣,所以 因此,存在ε>0,使得0 為了敘述方便,記為 注1定理1分別改進了文獻[2,7-8]的引理2.2,定理2.1和引理2.2. 這是因為矩陣A是嚴格對角占優矩陣可得dk<1.文獻[8]指出ri≤dk<1.另易證|mki|≤ri.事實上, 因此,若A是行嚴格對角占優的M-矩陣,則A-1=(bij)滿足 j≠i,j∈N. 定理2若A=(aij)∈Rn×n是行嚴格對角占優的M-矩陣,則A-1=(bij)滿足 證明一方面,由A是M-矩陣知:A-1=(bij)≥0.由AA-1=I得 即 于是 另一方面 由A=(aij)∈Rn×n是行嚴格對角占優的M-矩陣知 于是 因此 定理3若A=(aij)∈Rn×n是M-矩陣,且A-1=(bij)是雙隨機矩陣,則 所以A是嚴格對角占優矩陣.由定理1知 即 2.2M-矩陣與其逆的Hadamard積的最小特征值下界的估計式在文獻[1-2,5-8,12]中分別給出了M-矩陣A與其逆矩陣A-1的Hadamard積的最小特征值下界的估計式為(1)~(7)式.下面給出M-矩陣A與其逆矩陣A的Hadamard積的最小特征值下界新的估計式. 定理4若A=(aij)∈Rn×n是M-矩陣,且A-1=(bij)是雙隨機矩陣,則 (10) 證明1) 若A是不可約的,因為A-1是雙隨機矩陣,所以由引理2知 aii>1,i∈N. 所以 因此,矩陣A是一個嚴格對角占優矩陣.設 則對于?j∈N,j≠i有 因此,存在實數γji(0≤γji≤1)使得 所以 令 由A是不可約矩陣得 設A°A-1的特征值為λ,由引理3知,存在i0∈N得 因此 (ai0i0-vi0Ci0)bi0i0=(ai0i0-vi0Ri0)bi0i0≥ 2) 若A是可約的M-矩陣,則存在置換矩陣P使得 其中Ai1i1,Ai2i2,…,Aisis是不可約方陣.不失一般性,可假設A是塊上三角形式 其中Ai1i1,Ai2i2,…,Aisis是不可約方陣,于是A-1仍為塊上三角矩陣.因為 所以當A可約時,由1)的證明過程知,(10)式仍然成立. 定理5設矩陣A=(aij)∈Rn×n是M-矩陣,且A-1=(bij)是雙隨機矩陣,則 證明因為 且 由mki≤ri,得0≤vji≤mji,0≤vi≤mi,所以 aii-viRi≥aii-miRi≥aii-Ri>0. 因此 注2定理5指出,本文的定理4比文獻[8]的定理3.2更加接近于q(A°A-1). 定理6設矩陣A=(aij)∈Rn×n是M-矩陣,則 因此,為了方便和不失一般性,設A是不可約且A-1是雙隨機矩陣. 由A-1是雙隨機矩陣和引理2得:對于?i∈N有 且q(A°A-1)=q((A°A-1)T)=q(AT°(AT)-1). 令(AT°(AT)-1)e=(q1,q2,…,qn)T,則 于是 由引理5知 因此 2) 當A是可約的M-矩陣時,證明與定理4的2)類似的方法可以證(11)式成立. 推論若矩陣A=(aij)∈Rn×n是M-矩陣,則 推論表明定理6比文獻[8]的定理3.4更加接近于q(A°A-1). 本文得到的M-矩陣A與其逆矩陣A-1的Hadamard積最小特征值的下界,改進了文獻[8],而文獻[8]改進了文獻[7],文獻[7]改進了文獻[2-6].因此所得的結果是現有的結果提高.另外,新估計式的計算僅依賴于矩陣的元素.最后用數值算例表明文中得到的估計式比現有的估計式更為精確. 下面給出數值算例以說明本文定理的正確性和有效性. 對于矩陣 顯然矩陣A是嚴格對角占優的M-矩陣,且A-1是雙隨機矩陣. 1) 對矩陣A的逆矩陣A-1=(bij)的非對角元上界的估計.根據文獻[3]的引理2.2得 (12) 把文獻[7]的定理1(a)和推論2.5相結合得 (13) 根據文獻[8]的引理2.2(a)得 (14) 根據定理1(a)得 (15) 由(12)~(15)式可看出,由定理1所得的結果比文獻[3,7-8]所得的結果能更好地估計A-1的非對角元. 2) 對逆矩陣A-1的對角元的估計.由文獻[7]的定理2.3和引理3.2,可知矩陣A-1的對角元的上界與下界的估計值為 0.341 9≤b11≤0.481 9; 0.340 4≤b22≤0.410 3; 0.341 9≤b33≤0.484 8; 0.340 4≤b44≤0.484 8. 由文獻[8]的引理2.3和定理3.1,可以得到矩陣A-1的對角元的上界與下界的估計值 0.363 6≤b11≤0.444 4; 0.352 9≤b22≤0.3871; 0.400 0≤b33≤0.400 0; 0.400 0≤b44≤0.400 0. 如果根據本文的定理2和定理3得到矩陣A-1的對角元的上界與下界的估計值 0.379 1≤b11≤0.423 3; 0.360 9≤b22≤0.375 0; 0.400 0≤b33≤0.400 0; 0.400 0≤b44≤0.400 0. 對以上結果進行比較,可知定理2和定理3比文獻[7-8]對矩陣A的逆矩陣A-1的對角元素的上界和下界更好地進行了估計. 3) 對A°A-1的最小特征值下界的估計,由Fiedler和Markham的猜想得:q(A°A-1)≥0.5.由文獻[7]中的定理3.1得:q(A°A-1)≥0.662 4;由文獻[8]中的定理3.2得:q(A°A-1)≥0.799 9;由本文定理4得:q(A°A-1)≥0.825 0,而q(A°A-1)的真實值為q(A°A-1)=0.975 5. 對以上結果進行比較,可知定理4的結果有效地改進了M.Fiedler和T.L.Markham猜想以及文獻[7-8]的結果. 致謝文山學院重點學科建設項目(12WSXK01)對本文給予了資助,謹致謝意. [1] Fiedler M, Markham T L. An inequality for the Hadamard product of an M-matrix and inverse M-matrix[J]. Linear Algebra and Its Applications,1988,101:1-8. [2] Yong X R, Wang Z. On a conjecture of Fiedler and Markham[J]. Linear Algebra and Its Applications,1999,288:259-267. [3] Song Y Z. On an inequality for the Hadamard product of an M-matrix and its inverse[J]. Linear Algebra and Its Applications,2000,305:99-105. [4] Yong X R. Proof of a conjecture of Fiedler and Markham[J]. Linear Algebra and Its Applications,2000,320:167-171. [5] Chen S C. A lower bound for minimum eigenvalue of the Hadamard product of matrices[J]. Linear Algebra and Its Applications,2004,378:159-166. [6] Xiang S H. On an inequality for the Hadamard product of an M-matrix or H-matrix and its inverse[J]. Linear Algebra and Its Applications,2003,367:17-27. [7] Li H B, Huang T Z, Shen S Q,et al. Lower bounds for the minimum eigenvalue of Hadamard product of an M-matrix and its inverse[J]. Linear Algebra and Its Applications,2007,420:235-247. [8] Li Y Y, Chen F B, Wang D F. New lower bounds on eigenvalue of the Hadamard product of an M-matrix and its inverse[J]. Linear Algebra and Its Applications,2009,430:1423-1431. [9] 黃榮. M-矩陣及其逆矩陣的Hadamard積最小特征值的下界估計[J]. 華東師范大學學報:自然科學版,2008(3):67-74. [10] 劉新. M-矩陣與其逆矩陣的Hadamard積最小特征值的新下界[J]. 四川理工學院學報:自然科學版,2010,2(25):15-17. [11] 盧飛龍,何希勤 . M-矩陣與其逆的Hadamard積的特征值下界[J]. 遼寧科技大學學報,2010,33(5):555-560. [12] 楊曉英,劉新. M-矩陣及其逆矩陣的Hadamard積最小特征值下界的估計[J]. 山東大學學報:理學版,2012,47(8):64-67. [13] 劉新,楊曉英. M-矩陣Hadamard積最小特征值的新下界[J]. 重慶師范大學學報:自然科學版,2013,30(2):53-55. [14] 馮海亮,伍俊良. 四元素矩陣特征值的一些估計定理[J]. 重慶師范學院學報:自然科學版,1997,14(2):48-50. [15] 黃廷祝,楊傳勝. 特殊矩陣分析及應用[M]. 北京:科學技術出版社,2003. [16] 陳景良,陳向輝. 特殊矩陣[M]. 北京: 清華大學出版社,2000. [17] Varga R S. Minimal Gerschgorin sets[J]. Pacific J Math,1965,15(2):719-729. [18] Sinkhorn R. A relationship between arbitrary positive matrices and doubly stochastic matrix[J]. Annals Math Stat,1964,35:876-879.

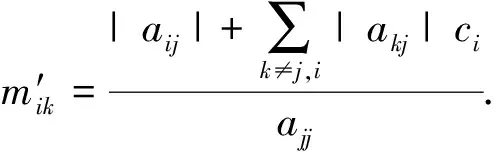
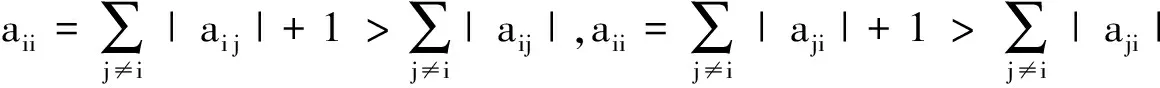

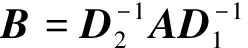

3 數值算例