指數保費原理下的廣義線性模型信度估計

趙 珍, 吳黎軍

(新疆大學 數學與系統科學學院， 新疆 烏魯木齊 830046)

信度保費定價是保險公司對保費的一個合理定價過程，依賴于保單組合的過去索賠經歷.最經典的信度理論是Buhlmann[1]信度理論，他建立了任意分布下的信度理論.同時，在保險精算中，許多信度理論都建立在指數分布族框架上，詳細內容可參考文獻[2-4].但是在這些信度理論中得到的保費沒有正的安全負荷性，是純保費，所以保險公司為了避免破產，必須引入恰當的保費原理來解決這一問題，也就是將經典信度模型中的平方損失函數修改為其他損失函數，文獻[5]給出了分位數損失函數、冪加權損失函數等許多損失函數下的保費原理.文獻[6]指出了指數損失函數下對應的指數保費原理的信度估計.

但是，在廣義線性模型中，對多水平費率的厘定同樣是信度理論定價的一個重要內容,也是非壽險精算中最普遍用的技術,即在給定水平下的保費可以用當前水平下的經驗數據來估計[7].Nelder和Verrall[8]首次把信度理論擴展到廣義線性模型框架下，他們證明了對于多水平因子的費率厘定具有相似的Buhlmann估計.與此同時，Nelder和Verrall還推導出了在具有普通費率因子時，單個多水平費率因子也能得到相似的信度估計.自20世紀90年代后期以來，關于多水平費率因子的信度估計受到了越來越多的精算學者的關注. Kass[9]等推廣了除多水平外還有普通費率因子的情況,得到了加權觀測值下的精確信度模型.Ohlsson 和Johansson[10]討論了基于指數分布族模型與廣義線性混合模型中隨機效應之間的關系；與此同時，Ohlsson 和Johansson[11]還使用另外一種方法，即在信度模型框架下引入固定效應，得到了相同的信度估計.Garrido和Zhou[12]首次把古典信度理論與廣義線性模型相結合，建立了相應的信度模型.但是以上這些廣義線性模型的信度估計都是在平方損失函數下建立的,所以對模型而言得到的保費同樣都是純保費,不具有正的安全負荷性,這樣保險公司注定會破產.為了解決這一問題,本文在考慮指數保費原理的基礎上,進一步利用指數損失函數的方法，把古典信度理論與廣義線性模型相結合來討論相應的信度估計．

1 模型的準備與假設

1.1 廣義線性模型

在古典線性回歸模型中，假設因變量服從正態分布，方差為常數，解釋變量通過線性相加關系直接影響因變量本身.而廣義線性模型假設因變量來自于指數分布族，其方差隨著均值而變化，解釋變量通過線性相加關系對因變量的期望值的某種變換產生影響.若Yi是第i個觀測值且服從指數分布族，則其密度函數可以表示為

式中：b(θi)，c(yi,φ,wi)為已知函數，φ>0對所有的觀察值具有相同的形式，wi為權重，b(θi)的二階導數存在且大于零.c(yi,φ,wi)與參數θi無關.觀察值Yi的均值和方差分別為

E(Yi)=b′(θi)，var(Yi)=φυ(μi)/wi

(1)

其中υ(μi)=b″(b′-1(μi))是方差函數.

1.2 信度模型

多水平因子的費率厘定是應用信度理論定價的一個重要內容. 給定水平下的保費可以用當前水平下的經驗數據來估計，這一過程主要借用廣義線性模型來實現.首先，我們只考慮一個單一的多水平因子的費率厘定.

設Yjt是在多水平j下的第t個觀察值的關鍵費率，j=1,2,…,J.Uj是在多水平j下的隨機效應.則基本模型為

E(eαYjt|Uj)=μαUj

(2)

其中E(Uj)=1，E(eαYjt)=μα，α>0為已知參數.

為了計算方便，令Vj=μαUj，E(Vj)=μα，則

E(eαYjt|Vj)=Vj

(3)

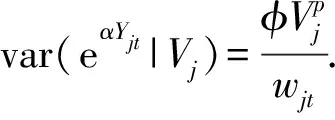
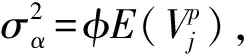
(4)

因此得到下面的假設.

假設1(a)隨機向量(Yjt,Vj)，j=1,…,J是獨立的.

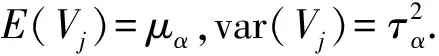
(c)在Vj的條件下，Yjt相互獨立，均值和方差滿足(3)和(4)式.

定義1 指數損失函數為

L(x,p)=(eαY-eαp)

(5)

其中α>0是已知參數.

2 信度理論

2.1 信度估計

類似于經典的信度理論，信度估計可以定義為：將估計限定在某些線性函數類中.在損失函數(5)式下，求解下面的最小化問題

minE(c0+∑tcteαYt-eαp)2

(6)

為求上述最小化問題，我們先給出下面的引理.

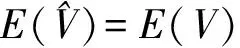
(7)

(8)

證明令Xt=eαYt，求解最小化問題(6)式就是求解minE(c0+∑tctXt-V)2.

令h(X)=c0∑tctXt，則

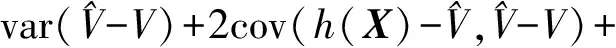
[E(h(X)-V)]2

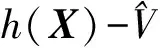
則

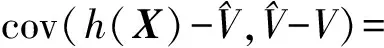
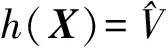
有最小值.

定理1在假設1成立時，求解最優化問題(6)得到的最優估計為

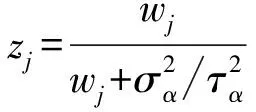
證明根據引理1，只需證明

滿足(7)和(8)式.因

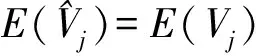
cov(Vj,eαYjt=cov[Vj,E(eαYjt|Vj)]=

當s≠t時，cov(eαYjs,eαYjt)=E[cov(eαYjs,eαYjt|Vj)]+cov[E(eαYjs|Vj),E(eαYjt|Vj)]=0+

當s=t時，cov(eαYjs,eαYjt=var(eαYjt=

因此

2.2 結構參數的估計

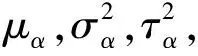
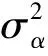
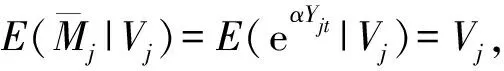
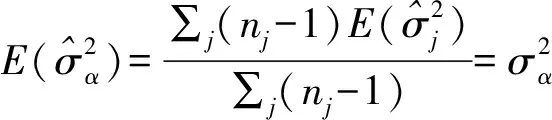
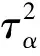
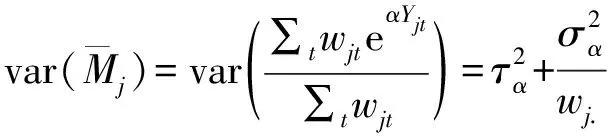
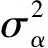
因此

則

3 乘法模型中的信度估計

下面考慮如何把廣義線性模型和信度理論聯合起來同時得到普通費率因子和多水平因子的估計.在這里，我們只考慮一個單一的多水平因子，普通費率因子可以是任意多個.例如房屋保險，考慮房子的類型、建筑面積和地理區域.把房子的類型、建筑面積作為普通費率因子，地理區域作為多水平因子，則(2)式可以推廣為

(9)

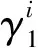
設Yijt是關鍵費率，則(9)式可以被推廣到有R個普通費率因子的情形，即

(10)

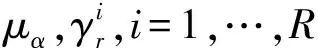
E(eαYijt|Vj)=γiVj

(11)

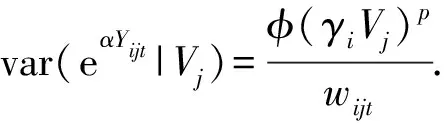
(12)

則得到下面假設.

假設2(a)隨機向量(Yijt,Vj)，j=1,…,J獨立.

(b)Vj，j=1, …,J是同分布.E(Vj)=μα，

(c)對于任何j，在Vj的條件下，Yijt是相互獨立的，且均值和方差滿足(11)和(12)式.

令

(13)

則

(14)

定理4在假設2成立時，保費p的估計為

隨機效應為

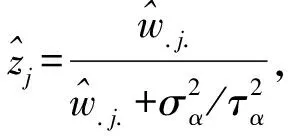
4 結束語

本文利用信度理論的方法，考慮在指數保費原理下信度理論與廣義線性模型中隨機效應之間的關系來討論相應的信度估計，分別得到了在該指數保費原理下多水平因子以及普通費率因子與多水平因子相結合的信度保費估計，并且給出了結構參數的估計. 結果表明，所得的信度公式具有經典的信度形式，這一結果推廣了經典的信度模型．

[1] Bühlmann H． Experience rating and credibility [J]． Astin Bulletin，1967,4(3)：199-207．

[2] Bühlmann H, Gisler A．A course in credibility theory and its applications [M]. Netherlands: Springer,2005.

[3] Sundt B．An introduction to non-life insurance mathematics [M]. 3rd version. Ann Arbor: University of Michigan, 1999.

[4] Virginia A. Effective actuarial methods [C]// Zimmermann. Proceedings of the 6th International Conference on Knowledge Management: Projects, Systems and Technologies. Bucharest: Economic Research Department, Federal Reserve Bank of St. Louis, 2011：39-44.

[5] Heilmann W R. Decision theoretic foundations of credibility theory [J]. Insurance: Mathematics and Economics, 1989,8:77-95.

[6] 溫利民，吳賢毅.指數保費原理下的經驗厘定[J]. 中國科學，2011，41(10)：861-876.

[7] Nelder J A，Wedderbum R W M. Generalized linear models [J]．Journal of the Royal Statistical Society, 1972, 135(3): 370-384．

[8] Nelder J A，Verrall R J．Credibility theory and generalized linear models [J]. Astin Bulletin，1997，27(1)：71-82.

[9] Kass R, Dannenburg D, Goovaerts M J . Exact credibility for weighted observations [J]. Astin Bulletin, 1997, 27(3): 287-295.

[10] Ohlsson E, Johansson B．Combining generalized linear and models and credibility models in practice[J]．Scandinavian Actuarial Journal，2003, 4: 301-314．

[11] Ohlsson E，Johansson B．Credibility rating in a multiplicative tariff [J]．Astin Colloquium International Actuarial Association Brussels, 2004, 34(7)：1-15.

[12] Garrido J, Zhou J. Credibility theory for generalized linear and mixed models [R]. No.5/06, Montreal, Quebec: Concordia University, 2006.