GPmL-stability of the Rosenbrock methods for the systems of differential equations with many delays

LU Zhiwen

(School of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

1 Introduction

We consider the stability behavior of the Rosenbrock method in the solution of the system of differential equations with many delays:

y′(t)=Ly(t)+M1y(t-τ1)+M2y(t-τ2)+…+Mmy(t-τm),t≥0,

(1)

y(t)=φ(t),t≤0.

(2)

wherey(t) denotes thed-dimension unknown vector (y1(t),y2(t),…,yd(t))T.

L,Mi,1≤i≤mare constant complexd×dmatrices,τi>0,1≤i≤mare constant delays,φ(t) is a given vector- value function andy(t)is unknown whent>0.

Many authors have considered the stability behavior of numerical methods for systems of delay differential equations.The Rosenbrock methods can easily be programmaed.Hairer et al.[1]considered the constructions and Piche[2]considered the stability of the Rosenbrock methods.Liu and coworkers[3-4]investigated the stability of the Rosenbrock methods.

The purpose of this paper is to investigate theGPmL-stability of the Rosenbrock methods for systems of differential equations with many delays.We shall prove that the Rosenbrock methods areGPmL-stable if and only if they areL-stable.

2 Basic Preparation and Lemma

Assuming an exponential solution of (1)(2) in the form

y(t)=ξ·eζt(ξ∈cd),

we have the characteristic equation of (1)(2)

det(ζI-L-M1e-ζτ1-M2e-ζτ2-…-Mme-ζτm)=0.

(3)

The following lemma guarantees that the system is asymptotically stable.

Lemma2.1[5]Assume that the coefficients of (1) satisfy

(4)

(5)

Then all roots of the characteristic equation (3) have negative real parts and the system of (1)(2) is asymptotically stable,i.e.

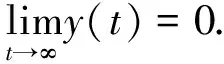
Now we give the stable definitions of numerical methods.

Definition2.2[6]IfL,Mi1≤i≤msatisfy (4)(5) in Lemma 2.1,then a numerical method is said to bePm-stable if the numerical solutionynof (1)(2) satisfies.

(6)

Definition2.3[6]A numerical method is said to beGPm-stable if the condition of the former definition ofPm-stability is satisfied for arbitrary positive stepsizeh.

3 GPm-stability of the Rosenbrock methods for DDEs

For the general Rosenbrock methods for the DDEs (1)(2),by the Lagrange interpolation,we have

(7)

(8)

where

(9)

(10)

Here

(11)

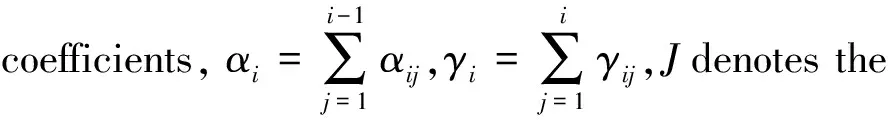
We apply the Rosenbrock methods (7)(8) to (1)(2),and get

So we can get the characteristic equation

(12)

where

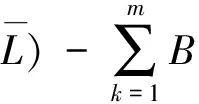
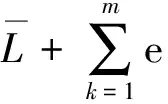
T3(z)=-zn(bT?Id),

T4(z)=Id(zn-zn-1).

Lemma3.1[7]If det[T1(z)]≠0,then (12) is equivalent to

(i) |α(z,δi)|≤1,(|z|=1,0≤δi<1) if and only ifr≤s≤r+2;

(ii) ifr+s>0,r≤s≤r+2,|z|=1,0≤δi<1,then |α(z,δi)|=1if and only ifz=1.

Lemma3.3[3]LetA=B,r≤s≤r+2 and (4)(5) hold.Then the Rosenbrock method (7)(8) for the delay differential equations (1)(2) isGPm-stable if and only if the corresponding Rosenbrock methods for ODEs areA-stable.

4 GPmL-stability of the Rosenbrock methods for DDEs

We consider the test equations (1)(2).

Lemma4.1[7]For the characteristic equation (3),ifLandMk(1≤k≤m) satisfy (4)(5) and the following equatity (P):

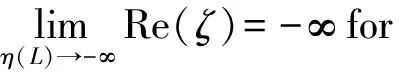
Definition4.2[6]IfLandMi(1≤i≤m) satisfy (4)(5) and the condition (P),then a numerical method is said to bePmL-stable if and only if it isPm-stable and the numerical solutions {yn} of (1)(2) satisfy.

(13)

whereyn～y(tn),tn=nh,mih=τi,1≤i≤m,τi>0 are constant delays,mi≥1,1≤i≤mare natural numbers.

Definition4.3[6]A numerical method is said to beGPmL- stable if and only if it isGPm-stable and (13) holds for anyh>0.

Theorem4.4LetA=B,r≤s≤r+2,andL,Mk(k=1,2,…,m) satisfy (4)(5) and (P).Then the Rosenbrock methods for the DDEs (1)(2) areGPmL-stable if and only if the corresponding Rosenbrock methods for ODEs areL-stable .

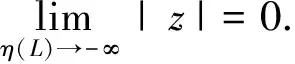
Let

(14)

whereλ(A) denotes the eigenvalue of the matrixA.

Then

(15)

Let

Then (15) implies

(16)

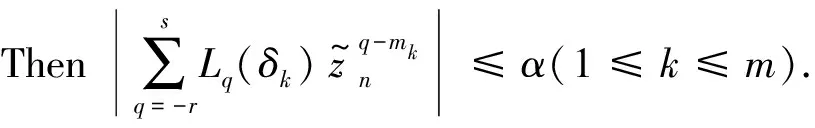
Thus

Since

Then (16) can be written in the form

From the condition(P),we have

Then

forn≥N0.

From Lemma 3.1,

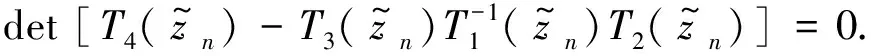
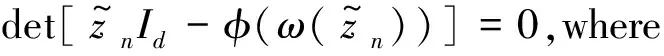
By the Spectral Mapping Theorem,we get

Then from the L-stability of the Rosenbrock methods,we have

and

Thus

:

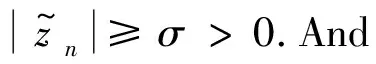
[1] HAIRER E,NΦRSETT S P,WANNER G.Solving ordinary differential equations[M].New York:Spring Press,2000.

[2] ROBERT PICHE.An L-stable Rosenbrock method for step-by-step time integration in structural dynamics[J].Comput Methods Appl Mech Engrg,1995,126:343-354.

[3] CAO X N,LIU D G,LI S F.Asymptotic stability of rosenbrock methods for delay differential equations[J].J of System Simulation,2002,14(3):290-292.

[4] CHEN L R,LIU D G.Combined RK-Rosenbrock methods and their stability[J].Mathematica Numerica Sinica,2000,22(3):319-332.

[5] KUANG J X,TIAN H J.The numerical treatment of linear system with many delays:report of AMS[R].Kent State University:AMS,1995.

[6] KUANG J X.Numerical solution of delay differential equations[M].Beijing:Science Press,1999.

[7] LIN Q.Stability Analysis of Numerical Solution of Delay Differential Equations[D].Nagoya:Nagoya University,2003.

[8] HOUTIN’T K J.A new interpolation procedure for adapting runge-kutta methods to delay differential equations[J].BIT,1992,32:634-649.