基于擔保方信用風險的可轉債定價問題研究

傅 毅,張寄洲,仇亞尊

(1.上海師范大學 商學院, 上海 200234; 2.上海師范大學 數理學院, 上海 200234)

0 引 言

隨著債券市場的發展,債券市場上出現了多種債券衍生產品,如可轉換債券等.可轉換債券是20世紀7,80年代興起的一種混合金融產品,目前,已成為中國證券市場研究的熱點之一.可轉換債券是指持有者可以在一定時期內按一定比例或價格轉換成一定數量的另一種證券的債券,通常轉換為發行公司的普通股票,一般具有較低的票面利率.從本質上講是在發行公司債券的基礎上,附加了一份期權,并允許購買人在規定的時間范圍內將其購買的債券轉換成指定公司的股票.可轉債具有債權和期權的雙重特征,并具有如下性質: (1) 債權性: 與其他債券一樣,可轉債也有利率和期限,投資者持有到期可以收取本息.(2) 股權性: 可轉債轉換成股票后,原債券持有人變為公司的股東,可參與公司的經營與紅利分配.(3) 可轉換性: 債券持有人可以按約定的條件將債券轉換成公司股票,如果債券持有人不想轉換,則可以繼續持有直到期滿收取本息,或者在流通市場出售變現.如果持有人看好發債公司股票的增值潛力,則可按約定的條件轉換成股票,發債公司不得拒絕.

近年來,許多學者主要從以下幾個方面研究了可轉債的定價等相關問題.

隨著Black-Scholes-Merton期權定價的模型的建立,一些學者在期權定價模型的基礎上對可轉債進行定價.Ingersoll(1977)[1]、Brennan和Schwartz(1977)[2]最早對可轉債的定價問題進行了理論研究,他們通過對公司的市值所滿足的隨機過程來研究可轉債的定價.不同于前面兩篇文章,Brennan和Schwartz(1980)[3]將利率的波動性考慮進了可轉債的定價中,并利用數值計算得出了可轉債的定價.Barone(2003)[4]等人又在以上模型的基礎上建立了關于標的資產和利率的雙因素模型.Toshikazu(2006)[5]等從另一個角度對可轉債進行了定價,將可轉債分解成兩部分,一部分是純債券價值,另一部分是轉換的期權價值,把未來的債券利息和本金的現值以及認股權證的現值相加得到可轉債的理論價值,并用Monte Carlo方法給出了帶有重置條款的可轉債的定價.

由于發行公司存在信用風險,所以把信用風險考慮進債券的定價中更貼近于現實.目前,研究信用風險主要有兩種方法：結構化方法和約化方法.結構化方法是把債券看成關于公司資產的看跌期權,但通常公司的資產情況并不能準確得到.而約化方法則是把公司的破產事件看成是一個外在的泊松過程,用第一次發生跳的時間作為公司的破產時間,其中泊松過程的強度可以從市場相關的數據推得.Kostas(1998)[6]等對帶有信用風險的可轉債進行了定價.Ayache(2003)[7]等利用對沖的思想通過構造投資組合對帶有信用風險的可轉債進行了定價.Wang(2010)[8]等人對帶有信用風險的永久可轉債進行了定價.

為了吸引投資者,發行公司在發行可轉債時往往設計一些附加條款.Kyoko(2010)[9]等分析了帶有可贖回和可回售條款的可轉債的定價,探索了贖回和回售的實施邊界,并研究了可贖回和回售條款對可轉債的價值和最優策略的影響,Fahuai(2011)[10]等對可轉債定價的自由邊界問題進行了研究,證明了變分不等式的解的存在性和唯一性,并且得到了自由邊界的單調性、有界性和光滑性等性質.Toshikazu(2006)[5]等研究了帶有重置條款的可轉債定價.熊思燦(2010)[11]等給出了附有巴黎期權特性的重置條款的可轉債定價模型,并采用有限差分方法求解模型.

另外,由于發行債券的公司都存在潛在的違約風險,而公司的信用等級對可轉債的價格有著重要的影響,所以發行公司往往通過信用增級的方式來提高可轉債的價格,其中信用增級方式中第三方擔保得到了廣泛的應用.任學敏(2009)[12]等用約化方法對有第三方擔保的企業債券進行了定價,得到了在擔保的情形下企業債券滿足的微分方程.劉易(2013)[13]等人在結構化模型的框架下,考慮了擔保公司和被擔保公司之間的相關性,得到了具有相關性的第三方擔保的公司債券所滿足的偏微分方程.

如上所述,考慮帶有擔保的可轉債的定價問題具有重要的現實意義.本文作者在約化模型的框架下對可轉債進行了定價,并考慮了可轉債的擔保方可能違約的情況,運用偏微分方程的方法得到了有擔保的可轉債的定價公式.文章的第一部分對模型做了一些假設，第二部分利用對沖技巧分別就擔保公司是否違約兩種情況建立了可轉債的數學定價模型，并在文章的第三部分對模型求解,最終得到可轉債的顯式解，第四部分對模型的參數進行了分析.

1 基本假設

假設1A公司發行了零息票可轉換債券,到期日為T,公司B為其作擔保.

假設2若發行公司A破產,其可轉債投資人的損失將由擔保公司B承擔.但如果擔保公司先于發行公司破產,則擔保失效.

假設3發行公司和擔保公司的破產是由不可預料事件引發的,違約強度分別為λ1,λ2,違約時間分別記為τ1,τ2.

假設4用Poisson過程的第一次跳來刻畫違約,Poisson過程在時間段[s,t]發生k次跳的概率為:

設τ為第一次跳的時刻,則公司在[0,T]時間段內的違約概率為:

P(τ≤T)=1-P(τ>T)=1-e-λT.

假設5發行公司與擔保公司違約發生是相互獨立的.

假設6發行公司的股票價格S(t)服從幾何布朗運動:

dS(t)=μS(t)dt+σS(t)dW(t) .

其中μ為期望回報率;σ為波動率,且都為常數;W(t)為標準的布朗運動.

假設7發行公司違約后,其股價變化滿足:

S+=S-(1-η) .

其中η為常數,表示發行公司違約后,其股價下降的幅度,這里的違約表示廣義的違約,即發行可轉債的公司可能由于流動性等原因造成不能按時支付息票所導致的違約.

假設8不考慮可轉債的可贖回和可回售條款.

假設9假設持有人的轉換權只發生在到期日或違約日,轉換權行使時一份可轉債可轉換為k份股票.可轉債的連續票息率為q.

2 模型建立

利用Δ-對沖技巧,建立可轉債定價的數學模型.首先,構造投資組合：

Πt=Vt-ΔSt,

其中V是發行公司的可轉債的價值;S是發行公司的股票價格.

在沒有違約的情況下,在[t,t+dt]時間段內,投資組合的變化為：

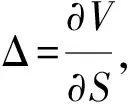
為了對[t,t+dt]時間段內的可轉債有無擔保進行刻畫,將可能發生的情況分為以下兩類:

情況一:有擔保時可轉債的定價模型

考慮違約的情況下,在[t,t+dt]時間段內,發行公司發生違約的概率為λ1dt.假設違約后,發行公司的股價滿足假設7.若發行公司先于擔保公司違約,則可轉債持有人有兩種選擇:

(1) 按可轉債面值F回收,回收率為R(0≤R≤1),其余部分由擔保公司承擔,債券持有人共獲得RF+(1-R)F即F.

(2) 執行轉換權,轉股得到的股票價值為kS(1-η1).

其中,η1為發行公司違約后,其股價下降的幅度.

這時投資組合Π的價值變化為:

(1)

由無套利原理得:

dΠ=rΠdt.

(2)

整理得:

這樣得到了有擔保情況下可轉債滿足的偏微分方程:

(3)

情況二:擔保失效時可轉債的定價模型

在[t,t+dt]時間段內,發行公司發生違約的概率為λ1dt.擔保公司發生違約的概率為λ2dt.若擔保公司先于發行公司違約,則發行公司違約后,可轉債持有人有兩種選擇權:

(1) 可轉債按面值回收,面值為F,回收率為R,持有人此時得到RF.

(2) 執行轉換權,轉股后得到的股票價值為kS(1-η2)(η2>η1).

其中,η2為發行公司違約后,其股價下降的幅度.

這時投資組合Π的價值變化為:

由無套利原理得:

這樣得到了擔保失效情況下可轉債滿足的偏微分方程:

(4)

以上兩種情況分析并得出了可轉債分別在有無擔保時滿足的定價方程,本研究中的定價思路是對每個可能的擔保公司的違約時刻τ2,確定相應的發行公司的可轉債的價格.

(1) 若0<τ2≤T,顯然當τ1∈[τ2,T]時,發行公司失去了擔保,其可轉債的定價方程為(4).當τ1∈[0,τ2]時,由于擔保公司未破產,則發行公司的可轉債扔有擔保,此時其定價方程為(3).

(2) 若τ2>T時,則在時間段[0,T]內擔保公司不破產,發行公司的可轉債有擔保,此時的定價方程為式(3).

下面計算各種情況的概率:

① 若0<τ2≤T且τ1∈[0,τ2],此時可轉債有擔保,則其發生的概率為:

(5)

② 若0<τ2≤T且τ1∈[τ2,T],此時可轉債無擔保,則其發生的概率為:

(6)

③ 若τ2>T,此時可轉債有擔保,其發生的概率為:

P3=P(τ2>T)=e-λ2T.

(7)

3 模型的求解

在這一節中,將分別求解出偏微分方程(3)和(4).首先,解方程(3).

作變換x=lnS,τ=T-t,定解問題(3)轉化為常系數拋物型的Cauchy問題:

作函數變換:V=Ueατ+βx,通過選取適當的α,β,使上式轉化為非齊次熱傳導方程:

(8)

其中

為求解式(8)首先求解以下齊次熱傳導方程的柯西問題:

(9)

柯西問題(9)的解為:

(10)

然后,再求非齊次熱傳導方程具有齊次初始條件的柯西問題:

(11)

得到柯西問題(11)的解為:

(12)

最后由疊加原理,由(10)及(12)就得到柯西問題(8)的解為:

整理得:

其中,

(13)

變換回到原變量V(S,t),得到有擔保的情形下可轉債的價值V1(S,t)為:

其中,

(14)

同理可解方程(4):

其中,d1,d2同上式(13)

變換回到原變量V(S,t),得到無擔保的情形下可轉債的價值V2(S,t):

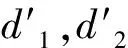
最后得到了可轉債的價值V(S,t)為:

V(S,t)=(P1+P3)V1(S,t)+P2V2(S,t).

4 數值分析

本文的前一部分中,作者運用偏微分方程的方法得到了考慮擔保方信用風險的可轉債的顯式解,接下來分析模型中一些參數對可轉債價值的影響.

圖1為不同時刻與股價所對應的可轉債的價值。

圖1 可轉債的價值V與時間t股票價格S的關系圖

圖2為發行公司的違約強度λ1對可轉債價值的影響.由圖2可看出,隨著發行公司的違約強度λ1的增大可轉債的價值變小.這是因為當發行公司的違約強度變大時,公司的破產概率變大,從而增加了可轉債持有者的可能損失,所以隨著發行公司的違約強度λ1的增大可轉債的價值變小.

圖3和圖4為擔保公司的違約強度λ2對可轉債價值的影響.由圖3可以看出當發行公司的違約強度λ1=0.05時,擔保公司的違約強度λ2越大可轉債的價值越小,成反向關系.同時也可以看出擔保公司的違約強度λ2的變化對可轉債的價值影響較小.這是因為在發行公司違約概率較小的情況下,擔保公司的違約強度的變化對可轉債的影響較小.而由圖4可以看出當發行公司的違約強度λ1=0.3時,擔保公司的違約強度λ2越大可轉債的價值越小,成反向關系,且擔保公司的違約強度λ2的變化對可轉債的價值影響較大,即當發行公司的違約強度較大時擔保公司對可轉債的價值起的作用會變大.

圖5為無風險利率r對可轉債價值的影響.由圖5可以看出,隨著無風險利率r的增大可轉債的價值變小.當股票價格遠高于轉股價格時,可轉換公司債券受市場利率影響較小,若價格較低時,可轉換公司債券對市場利率變動非常敏感,且成反向關系.

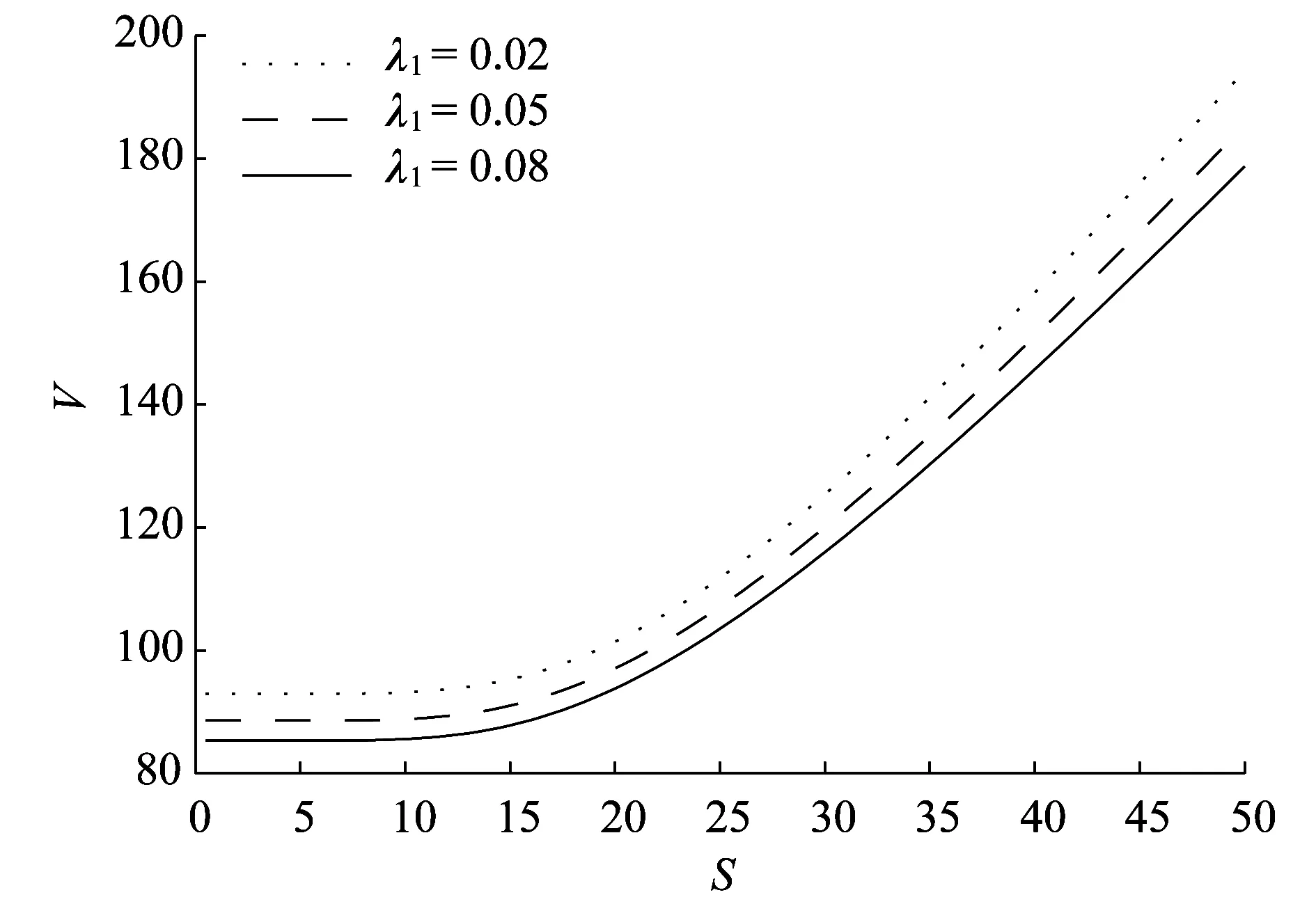
圖2 發行公司的違約強度λ1對可轉債價值的影響

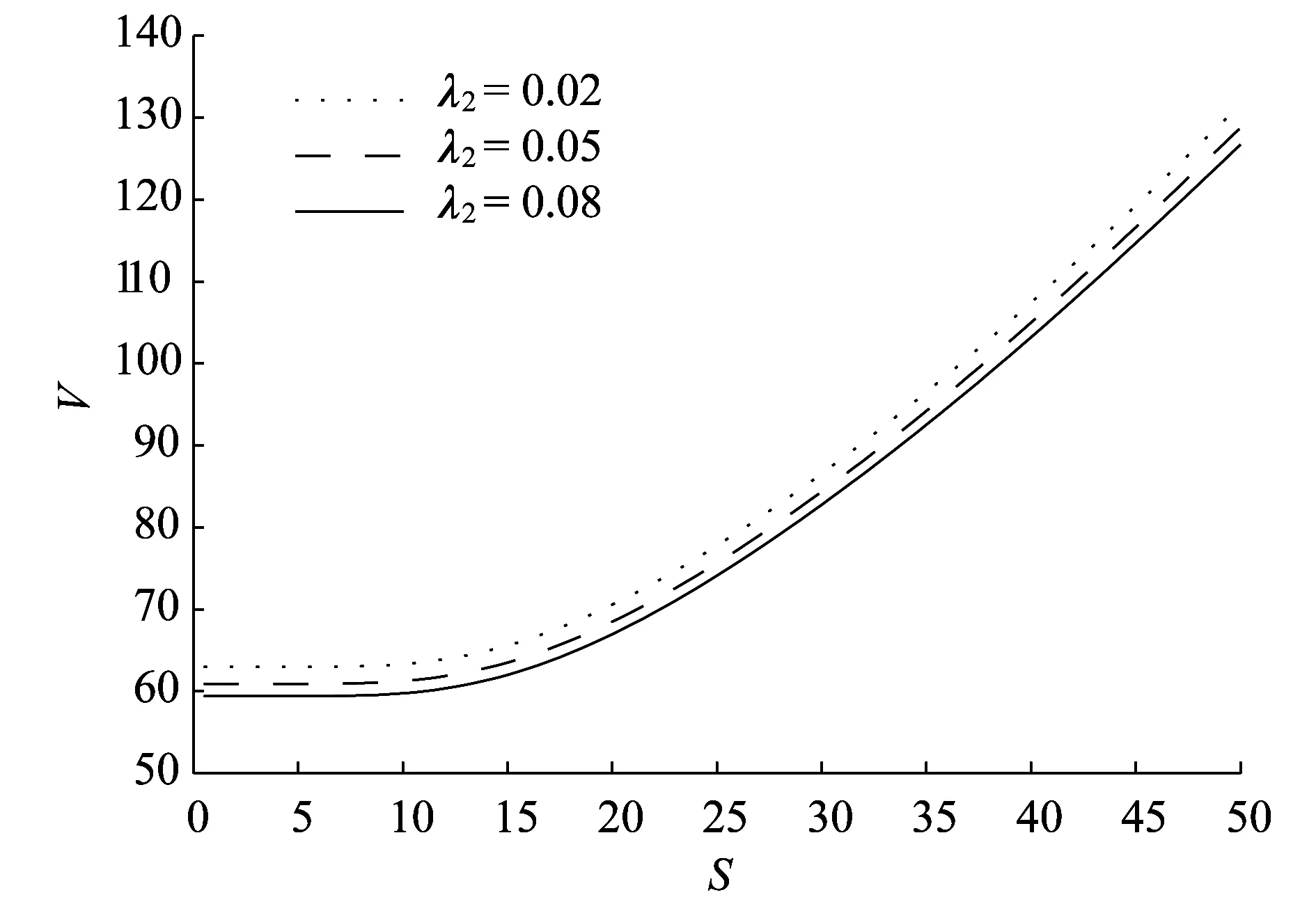
圖4 λ1=0.3時擔保公司的違約強度λ2對可轉債價值的影響

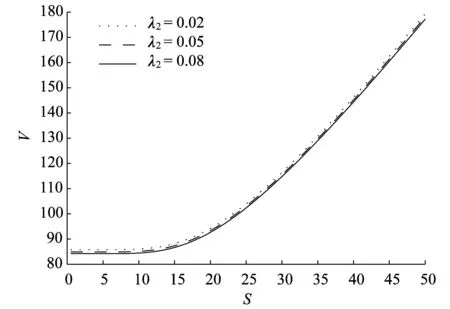
圖3 λ1=0.05時擔保公司的違約強度λ2對可轉債價值的影響

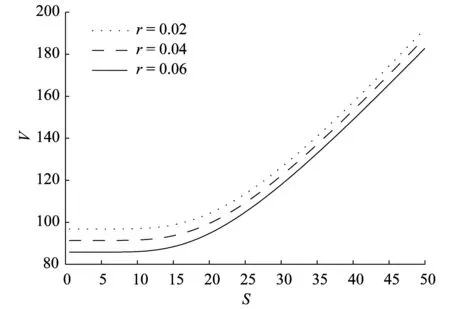
圖5 無風險利率r對可轉債價值的影響

圖6為股票的波動率σ對可轉債價值的影響.由圖6可以看出,隨著波動率σ的增大可轉債的價值變大.這是因為股票的波動率越大,可轉債的投資者獲得收益的可能性就越大,所以可轉債的價值就越大.

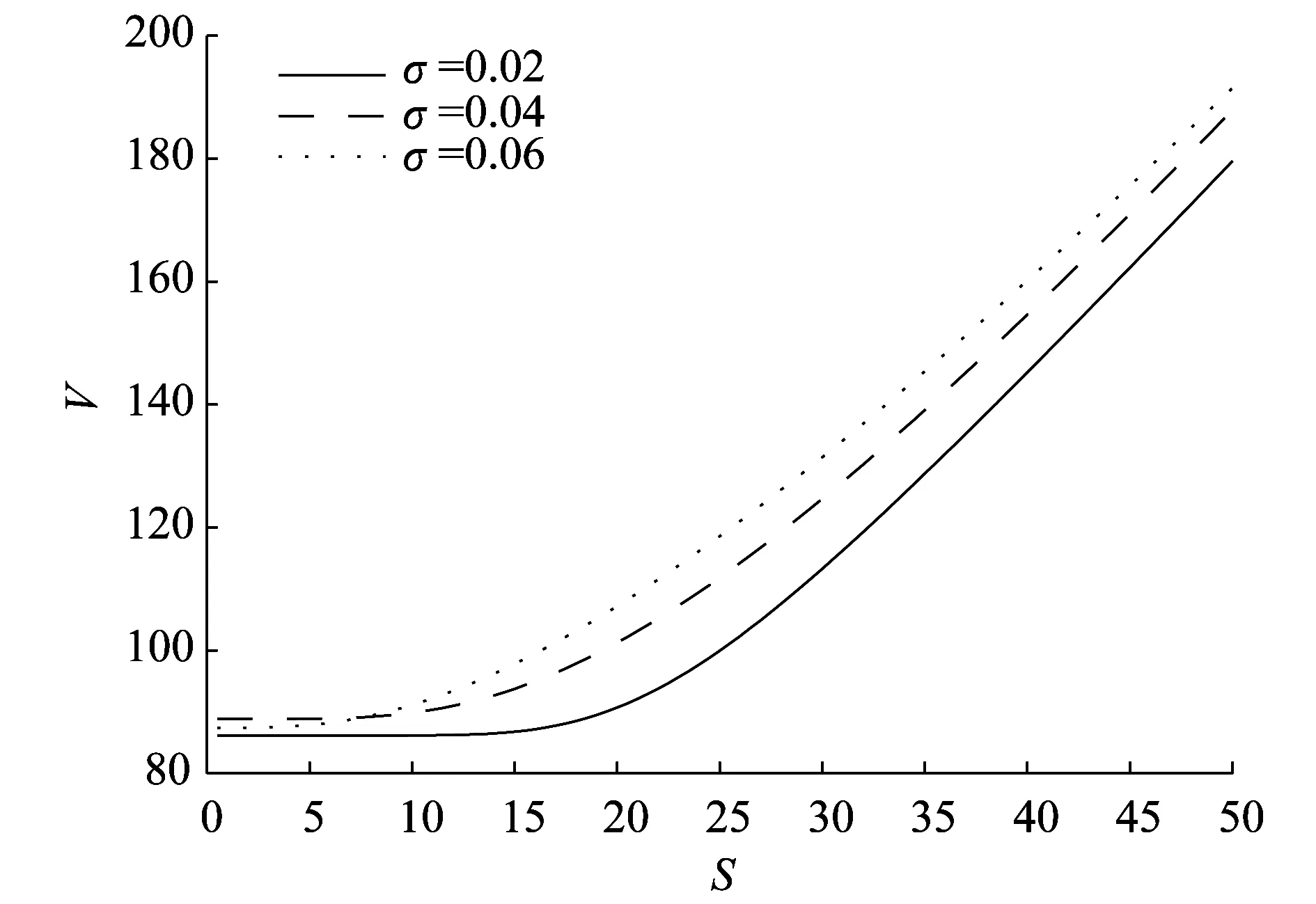
圖6 波動率σ對可轉債價值的影響

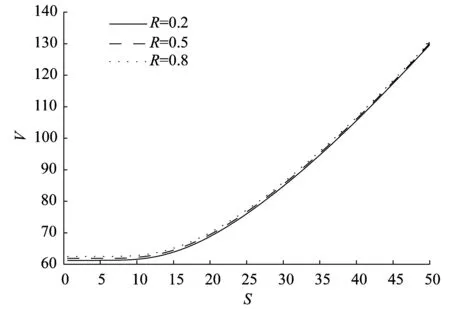
圖7 發行公司破產后不同的回收率R對可轉債價值的影響

圖7為發行公司破產后不同的回收率R對可轉債價值的影響.由圖7可以看出發行公司破產后的回收率越高可轉債的價值越大.同時也可以看出發行公司破產后的回收率對可轉債的價值影響是比較小的.這是因為在發行公司違約概率較小的情況下,回收率的變化對可轉債的影響較小.

圖8為可轉債不同的票面利率q對可轉債價值的影響.由圖8可以看出在其他條件相同的條件下,票面利率與可轉債價值成正向關系,可轉債的票面利率越高可轉債的價值越大,反之亦然.

圖9為可轉債不同的轉股率k對可轉債價值的影響.由圖9可以看出在其他條件相同的條件下,轉股率越高,轉股價越低,股票買權執行價格就越低股票買權的價值就越高,可轉債的價值就越高.

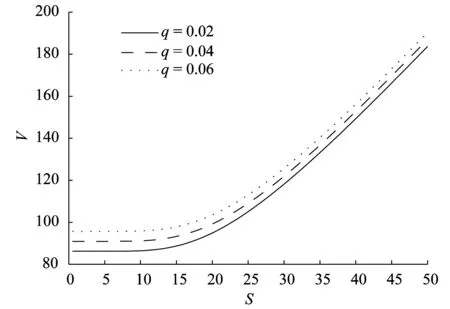
圖8 票面利率q對可轉債價值的影響

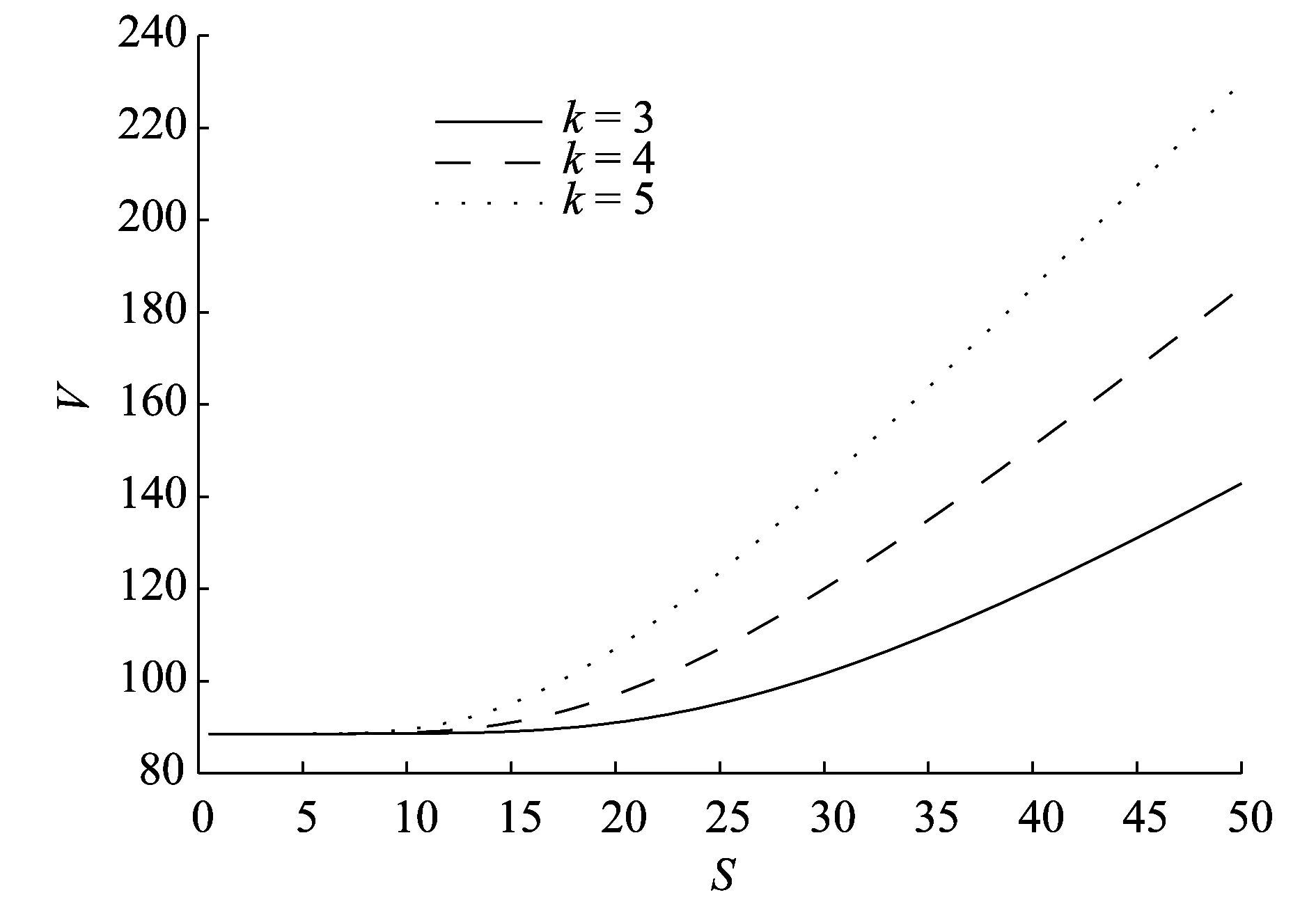
圖9 轉股率k對可轉債價值的影響

5 結 論

本研究是在AFV模型的基礎上進行了改進,研究分析了有擔保的可轉債的定價,并考慮了擔保公司是否違約,針對不同情形建立了相應的數學模型,最終得到了擔保公司可能違約的情況下可轉債的定價公式的顯式解,并分析了擔保公司在破產和不破產兩種不同情形下對發行公司的可轉債價格的影響.

參考文獻:

[1] INGERSOLL JR J.A contingent-claims valuation of convertible securities[J].Journal of Financal Economics,1977，4:289-322.

[2] BRENNAN M J,SCHWARTZ E S.Convertible bonds:Valuation and optimal strategies for call and conversion[J].Journal of Finance,1977，32：1699-1715.

[3] BRENNAN M J,SCHWART E S.Analyzing convertible bonds[J].Journal of Finance and Quantitative Analysis,1980，15:907-929.

[4] BARONE ADESI G,BERMUDEZ A,HATGIOANNIDES J.Two factor convertible bonds valuation using the method of characteristics finite elements[J].Journal of Economic Dynamics and Control,2003，27:1801-1831.

[5] KIMURA T,SHINOHARA T.Monte carlo analysis of convertible bonds with reset clauses[J].European Journal of Operational Research,2006，168:301-310.

[6] TSIVERIOTIS K,FERNANDES C.Valuing convertible bonds with credit risk[J].Journal of Fixed Income,1998，8:95-102.

[7] AYACHE E,FORSYTH P A,VETZAL K R.The valuation of convertible bonds with credit risk[J].The Journal of Derivatives,2003，11:9-30.

[8] WANG L L,BIAN B J.Pricing of perpetual convertible bonds with credit risk under framework of reduce form[J].Journal of Tongji University,2010，6:935-940.

[9] KYOKO Y,KATSUSHIGE S.The valuation of callable-puttable reverse convertible bonds[J].Asia-Pacific Journal of Operational Research,2010，27:189-209.

[10] ZHOU Y,YI F H.A free boundary problem arising from pricing convertible bond[J].Applicable Analysis,2010，3:307-323.

[11] 熊思燦,錢永江,楊善朝.帶重置條款的可轉債定價模型及其實證研究[J].數學的實踐與認識,2010，2:33-39.

[12] 任學敏,萬凝.用約化方法對有第三方擔保的企業債券定價[J].同濟大學學報,2009，7:989-992.

[13] 劉易,任學敏,花虹.考慮相關性的第三方擔保價值的評估[J].同濟大學學報,2013，3:465-469.