大氣湍流下激光斜程通信誤碼率分析
吳 郁,周亞民,王忠思,劉 兵
(海軍士官學校三系,安徽蚌埠233012)
顯然,將式(2)、(3)代入式(4),就可以得到湍流條件下系統誤碼率的數學計算模型。
1 引言
在自由空間無線激光通信中,由于大氣湍流效應的影響,激光會產生光強閃爍、光束擴展等,這都使得接收光強產生隨機變化,進而引起接收信噪比降低,傳輸誤碼率增大,甚至會造成通信中斷,導致通信系統性能下降,影響通信系統的穩定性和可靠性[1,2]。
針對大氣湍流條件下的光波傳輸問題,國內外許多學者做了大量的研究。20世紀60年代開始,Tatarskii和 Chernov[3-4]基于 Rytov 近似,得出了研究水平空間傳播的Rytov方法。然而大量的實驗數據表明,Rytov方法僅適用于弱起伏區,對于中等強度以上的大氣湍流,Rytov方法不再適用。修正Rytov方法[5-6]將經典 Rytov方法擴展到中等湍流和強湍流區的閃爍研究,但依然只能解決大氣結構常數不變的水平空間傳輸問題。而對于光波斜程傳輸,Andrews[7]等研究了零內尺度條件下的弱起伏區中的高斯波束傳播問題。在此基礎上,國內一些學者[8-9]根據 ITU -R 大氣結構常數模型,將水平傳輸下的適用從弱起伏區到強起伏區的修正Rytov方法擴展到斜程傳輸,得到大氣湍流下,激光波束斜程傳輸的閃爍指數變化規律。
因此,在設計激光斜程通信系統鏈路時,必須充分考慮大氣湍流,特別是中等強度以上大氣湍流對通信系統傳輸誤碼率的影響。本文在以往的研究基礎上,研究大氣湍流下激光斜程通信誤碼率的計算方法,討論通信誤碼率隨不同系統參數的變化規律。
2 斜程信道的光強閃爍效應
在實際激光通信系統中,從發送端出來的激光經準直后,可以作為平面波來處理。而對于平面波的斜程傳播問題,一般認為在考慮了大氣結構常數隨高度的變化和斜程大氣結構常數對相關長度的影響后,可以將水平傳輸的Rytov方法應用于斜程傳輸[10]。在弱起伏情況下,Rytov方法的閃爍指數可以表示為[8,9]:
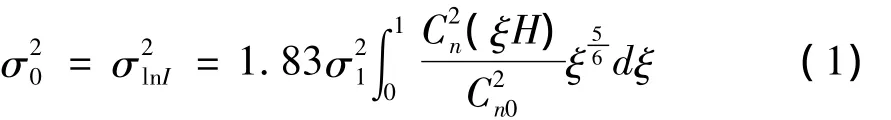

其中,σ2lnx,σ2lny分別為修正Rytov理論中大、小尺度湍流的對數振幅起伏方差。若不考慮內尺度,則平面波斜程傳輸的大、小尺度對數振幅方差可以分別表示為:
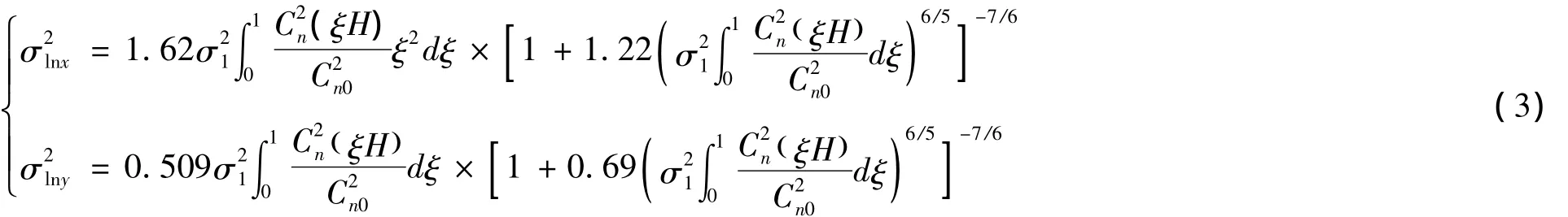
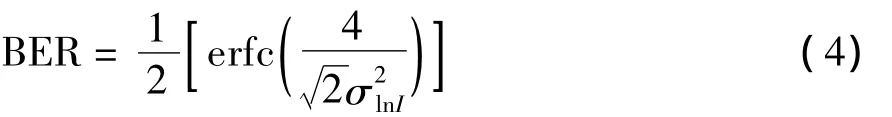
顯然,將式(2)、(3)代入式(4),就可以得到湍流條件下系統誤碼率的數學計算模型。
3 數值計算與分析
由式(3)可知,C2n廓線在很大程度上決定了對數振幅起伏方差σ2lnI的大小。由于C2n廓線在自適應光學、光干涉測量、光通信、激光傳輸等領域都有重要的應用,20世紀70 年代起,Wyngaar、Hufnagel、Abahamid等學者[11]先后總結了不同地區不同高度的C2n廓線,考慮到模擬計算的一般性,這里采用國際電信聯盟提出的ITU-R湍流大氣結構模型[12],它可以表示為:
大氣湍流引起的光強起伏,使得接收到的光強產生隨機變化,忽大忽小,這將導致通信誤碼率增大,嚴重影響自由空間無線激光通信系統的性能。而通信系統誤碼率與對數振幅起伏方差的關系可以表示為[2]:
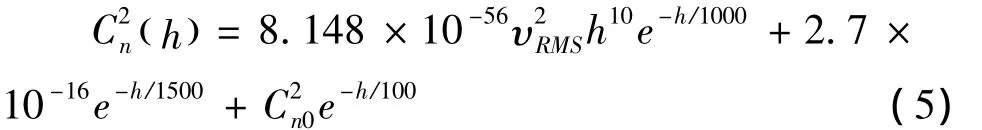
其中,υRMS表示垂直路徑風速,其與近地面風速υg的
不同近地面大氣結構常數、不同風速條件下,利用式(6)計算出的C2n隨高度h變化的關系曲線如圖1所示。從圖中可以看出,在ITU-R湍流大氣結構模型中,1 km高度以下,C2n的大小主要依賴于C2n0,基本不受風速υRMS的影響,隨著高度的增加,C2n逐漸減小,同時受C2n0影響也逐漸減弱;當高度達到1 km以上,C2n0對C2n的大小基本沒有影響;當高度達到約4 km以上,風速υRMS對C2n的影響很明顯。關系可以表示為
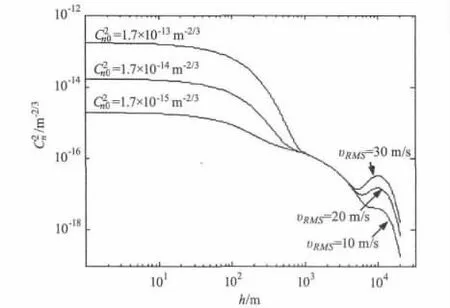
圖1 不同風速和近地面大氣結構常數下大氣結構常數隨高度的分布
結合式(3)、式(4)和式(5),可以計算出不同的近地面大氣結構常數條件下,激光斜程通信系統誤碼率隨通信高度的變化規律,計算中近地面大氣結構常數C2n0分別取三個典型值1.7 ×10-15m-2/3(弱湍流)、1.7 × 10-14m-2/3(中等湍流)、1.7 × 10-13m-2/3(強湍流),計算結果如圖2所示。可以看出,在系統其他參數不變的情況下,隨著通信高度的不斷增加,誤碼率總體上先是急劇增大,然后趨于平穩。對于C2n0=1.7 × 10-13m-2/3,在工作波長 λ =0.488μm 、天頂角θ=π/4、風速υRMS=30m/s條件下,通信高度達到1 km時,大氣湍流引起的通信誤碼率即上升到10-8,而通常要求激光通信系統誤碼率在10-9以下[9],可見,強湍流條件下,激光通信系統的有效通信高度受到嚴重制約,且隨著湍流強度的增大,通信的有效高度將逐漸減小。此外,近地面大氣結構常數對誤碼率具有明顯的影響,當地面大氣結構常數不同時,誤碼率進入平穩變化的高度也不同。
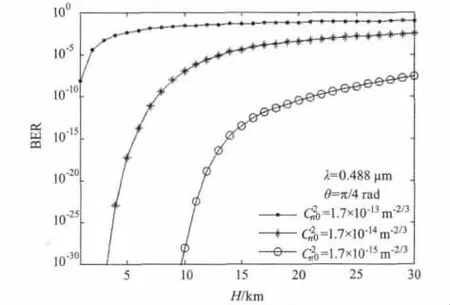
圖2 系統誤碼率隨通信高度的變化規律
圖3 給出了不同的近地面大氣結構常數條件下,系統誤碼率隨天頂角的變化規律。可以看出,在同一通信高度條件下,由于激光實際傳輸距離隨著天頂角的增加而增大,通信誤碼率也隨之提高。而在一定的通信誤碼率條件下,隨著湍流強度的增大,同一高度的空中平臺的激光通信系統在地面上的通信覆蓋范圍將越來越小,即地面有效通信覆蓋范圍將受到湍流強度的制約。并且,近面大氣結構常數越小,天頂角對通信誤碼率的影響也就越大。
工作波長也對通信誤碼率有很大影響,圖4給出了不同的近地面大氣結構常數條件下,系統誤碼率隨工作波長的變化規律。可以看出,隨著工作波長增長,通信誤碼率降低,即在一定的通信誤碼率條件下,通信系統的工作頻率范圍將受到湍流強度的制約。并且,波長越長,誤碼率隨波長變化越明顯。近面大氣結構常數越小,工作波長對通信誤碼率的影響也就越大。
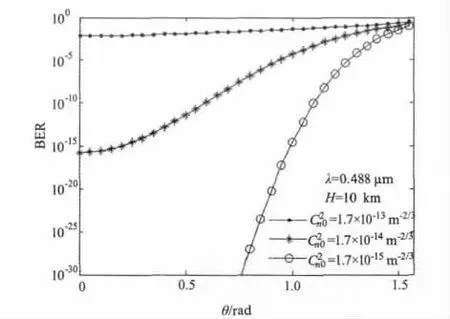
圖3 系統誤碼率隨天頂角的變化規律
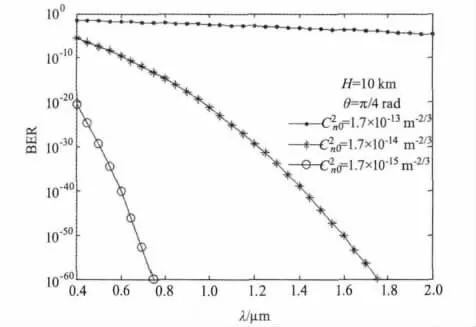
圖4 系統誤碼率隨工作波長的變化規律
此外,如前文所述,在ITU-R湍流大氣結構模型中,當高度達到4 km以上,風速υRMS對大氣結構常數有明顯影響,因此,當通信高度在4 km以上,風速也是通信誤碼率的一個影響因素。圖5給出了不同的近地面大氣結構常數條件下,系統誤碼率隨風速的變化規律。可以看出,相比于前面幾種參數,風速對通信誤碼的影響較小。對于強湍流,風速大小對誤碼率幾乎沒有影響,中等湍流時,誤碼率隨風速的增大而增大,但變化比較緩慢,而弱湍流時,隨著風速的增大,誤碼率變化較為明顯。
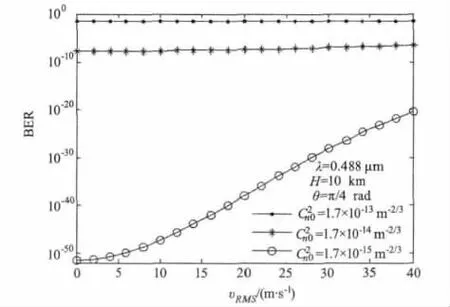
圖5 系統誤碼率隨風速的變化規律
4 結論
本文針對地空激光通信的實際情況,將修正Rytov方法應用于大氣湍流條件下的光波斜程傳輸研究。基于ITU-R大氣結構常數模型,建立了湍流條件下系統誤碼率的數學計算模型,對不同強度湍流信道的系統誤碼率進行了數值計算。數值計算結果表明:(1)大氣湍流強度是影響系統性能的決定性因素;(2)在相同強度湍流條件下,系統的誤碼率隨通信高度增加而增大,隨天頂角提高而增大,隨工作波長的增長而減小,隨風速的增大而增大。這些,可為自由空間激光通信的工程應用提供一定的理論分析和性能預測依據。
[1] HAO Botao,TONG Shoufeng. Receiving combination technology with detector array for spatial optical communication[J].Laser& Infrared,2013,43(5):487 -490.(in Chinese)郝博濤,佟首峰.空間激光通信探測陣列接收合并技術[J].激光與紅外,2013,43(5):486 -490.
[2] WANG Defei,CHU Zhenfeng,REN Zhenglei,et al.Influece of atmospheric turbulence on BER of laser communication system[J].Laser & Infrared,2011,41(4):390 -393.(in Chinese)王德飛,楚振峰,任正雷,等.大氣湍流對激光通信系統誤碼率影響的研究[J].激光與紅外,2011,41(4):390-393.
[3] Tatarskii V I.Wave propagation in a turbulent medium[M].New York:McGraw - Hill Book Company,Inc,1961.
[4] Chernov L A.Wave propagation in a random medium[M].New York:McGraw - Hill Book Company,Inc,1960.
[5] Andrews L C,Phillips R L,Hopen C Y,et al.Theory of optical scintillation[J].J.Opt.Soc.Am.,1999,16(6):1417-1429.
[6] Guo Lixin,Luo Zhimin,Wu Zhensen.A study of optical scintillation in the atmospheric turbulence by usingmodificationmodification of the Rytov method[J].Chin.J of Electronic,2001,10(3):300 -304.
[7] Andrews L C,Phillips R L,Yu P T.Optical scintillations and fade statistics for a satellite communication system[J].Appl.Opt.,1995,34(33):7742 -7751.
[8] WU Zhensen,LUO Zhimin,GUO Lixin,et al.Study on the scintillation of optical wave propagation in the slant path through the atmospheric turbulence[J].Chinese Journal of Radio Science,2002,17(3):254 -257.(in Chinese)吳振森,駱志敏,郭立新,等.湍流大氣中光波閃爍的斜程問題研究[J].電波科學學報,2002,17(3):254-257.
[9] YIXiuxiong,GUO Lixin,WU Zhensen.Study on the optical scintillation for Gaussion beam propagation in the slant path through the atmospheric turbulence[J].Acta Optica Sinica,2005,25(4):433 -438.(in Chinese)易修雄,郭立新,吳振森.高斯波束在湍流大氣斜程傳輸中的閃爍問題研究[J].光學學報,2005,25(4):433-438.
[10] Beran M J,Whitman A M.Scintillation index calculation using an altitude - dependent structure constant[J].Appl.Opt.,1988,27(11):2178 -2182.
[11] WANG Hongshuai,YAO Yongqiang,LIU Liyong.A review of atmospheric optical turbulence modeling research[J].Progress of Astronomy,2012,30(3):362 - 377.(in Chinese)王紅帥,姚永強,劉立勇.大氣光學湍流模型研究進展[J].天文學進展,2012,30(3):362 -377.
[12]ITU-R Document3J/31 - E.On Propagation data and prediction methods required for the design of space-toearth and earth-to-space optical communication systems[R].Budapest:Radio Communication Study Group Meeting,2001.

