時間-距離像消隱情況下彈道目標平動補償?

李星星,姚漢英,孫文峰,林澄清

(1.空軍預警學院，湖北武漢430019;2.94816部隊，福建福州350000)

0 引言

彈道目標微動特征的分析與提取是彈道導彈防御系統中真假彈頭識別的主要發展方向之一。近年來，基于微動效應的彈道目標特征提取與識別得到了深入的研究[1-3]。從公開文獻[4-8]看，現有的彈道目標微動特征提取方法大多假設目標平動已被精確補償，從而將特征曲線等效為正弦曲線或多個正弦分量的合成，進而應用時頻分析，擴展Hough變換[9]等方法實現微動參數估計與特征提取。但實際情況下，目標平動難以完全補償，這導致時間-距離像中提取的曲線附加了平動引起的調制項，這給后續的彈道目標特征提取與成像帶來了困難。文獻[10]基于彈道目標的微多普勒曲線極值點信息，利用最小二乘辨識方法實現了平動補償，文獻[11]基于彈道目標的微距離變化曲線，利用經驗模式分解方法實現了趨勢項的估計，進而完成了彈道目標平動補償，文獻[12]基于距離和差值序列信息完成了復雜運動目標擺動周期及平動參數估計;但上述方法要求微多普勒曲線和微距離曲線是連續的，在實際應用中，由于彈道目標的散射強度受視線角的變化而改變，其時間 距離像會出現消隱現象[13]，此時，該條件無法滿足。針對這一問題，本文提出了一種在時間-距離像消隱情況下實現彈道目標平動參數和進動頻率聯合估計的方法，實驗結果表明，此方法參數估計精度高且魯棒性較強。

1 導彈中段目標回波模型

設雷達發射的線性調頻信號為

式中，τi(t m)為t m時刻此散射點到雷達的距離時延。

設參考距離為Rref，將回波進行解線頻調處理后，在快時間域進行傅里葉變換并去除剩余視頻相位項和包絡斜置項后得到距離-時間域表達式為

式中，R為距離像中散射點位置;ΔR i(t m)為t m時刻此散射點到雷達視線投影距離與參考點到雷達距離之差，且有

式中，Rr(t m)為參考距離與彈道目標質心到雷達實際距離之差;r i(t m)為彈道目標第i個散射點在雷達視線上投影距離變化項，由散射點位置和微動引起。由式(3)知，完成距離壓縮后回波信號在距離像上聚焦為sinc函數，其峰值位置R=-ΔR i(t m)反映了該散射點與參考點之間的距離差。

中段彈道目標一般在大氣層外近地空間飛行，假設不考慮目標飛行過程中空氣動力作用以及其他天體對目標運動的影響，即只考慮地球引力作用，此時目標可視為二體運動，在短時間內，其軌道運動(即平動)可以采用勻加速模型來描述。理想條件下，為了實現高速運動補償，取彈道目標質心回波信號作為參考信號，則Rr(t m)=0，但實際應用中，彈道目標質心的回波信號是無法完全準確獲得的，通常只能通過測距得到R0的估計值，以及通過測速得到的v的估計值，因此實際構造的參考信號為從而有

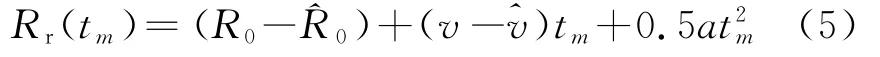
式中，a為彈道目標加速度。

彈道目標在中段慣性飛行時進動模型如圖1所示。圖中，彈頭為旋轉對稱錐體，其進動軸為Oz軸，進動軸與雷達視線確定的平面為Oyz平面，再根據右手定則建立Ox yz參考坐標系。設Ox′y′z′為彈體坐標系，彈頭繞其對稱軸Oz′以角速度ωs作自旋運動，同時Oz′軸繞Oz軸以角速度ω錐旋，進動角為θ。

圖1 錐體目標進動模型

設目標進動軸相對于雷達視線的姿態角為γ，目標相對于雷達視線的姿態角為β，則有[14]

式中，φ為零時刻彈頭頂部軌跡的圓心到彈頭頂部連線與x軸的夾角。

由圖2中的幾何關系可知，錐頂等效散射點A在雷達視線上的投影長度為

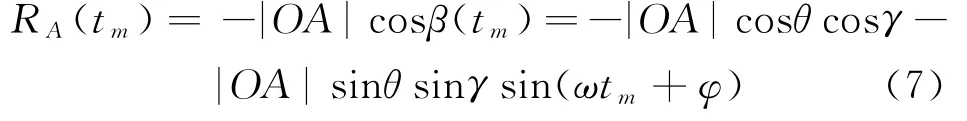
錐底邊緣散射點B在雷達視線方向上的投影長度為

在常見彈道目標的探測視角范圍(45°～135°)內，對上式近似可得

圖2 散射中心在雷達視線上投影模型

上式中最后一項通常比其他兩項小兩個數量級，為一極小量，可以忽略，因此散射點B徑向投影長度變化規律近似正弦變化[16]。綜合式(7)和式(9)可知，目標第i個散射點在雷達視線上投影長度隨時間變化關系可寫成

式中，φi為初始相位;A i，B i分別為微距離曲線振幅和基線。因此式(4)可以寫成

2 進動與平動參數聯合估計

2.1 微距離變化曲線提取與分離

微距離變化曲線的提取與分離主要包括以下三個步驟:

(2)運用目標檢測思想，對時間切片序列進行滑窗檢測，若窗口中心處的值為窗口中最大值，則認為檢測到散射點，進行幅度增強，其他值進行加權抑制，考慮到運算效率，窗長不宜過大，一般取窗長l=3，權值w=0[15]。利用矩陣C N×H記錄散射點在時間-距離像中的位置，其中N為距離像數量，H為一維距離像序列距離單元數。

(3)顯然由式(11)確定的曲線方程關于慢時間t m是可導的，但由于存在斷續現象，曲線只是局部連續的，本文運用航跡起始和航跡跟蹤的思想分離出斷續曲線[16]，將散射點位置的變化曲線等效為目標航跡。從C N×H中分離各散射點曲線的具體步驟為:

a)令i=1，得到C N×H中第i列大于閾值ε的局部極大值，記為P j(j=1，2，…，p)，p為量測點數，為每一個量測建立初始航跡起點，以P j為中心分別建立半徑為P r個距離單元的圓跟蹤門M j形成確認區域，從而建立P個候選目標航跡。

b)i=i+1，得到C N×H中第i列大于閾值ε的局部極大值，對任何落入確認區域的量測(利用多項式擬合局部連續的微距離曲線)外推得到下一個點P′j，并建立新的圓跟蹤門M′j形成新的確認區域。若沒有量測位于確認區域，則此候選目標航跡提前終止。若某量測沒有落入任何確認區域，則形成新的初始航跡起點，建立新的圓跟蹤門并形成確認區域，在下一幀距離像搜索新的可能航跡。

c)重復步驟b)，若暫時航跡中量測數達到3個，則認為航跡起始成功，然后進行航跡跟蹤。若航跡丟點則由前面的m1點的外推值代替，若航跡連續丟點數超過q1，則計算航跡包含的量測數，若量測數小于q2，則去除這一航跡，反之則終止并保留這條航跡，當i＞N時停止搜索。

d)設最后得到M m條航跡進行關聯處理得到各個散射點的微距離曲線方程ΔR i(t m)。

2.2 進動與平動參數聯合估計方法

式(11)中信號ΔR i(t m)可離散化為

式(13)中有四個未知參數，至少需要四個方程(四點坐標信息)才能求解，然而此類方程為超越方程直接求解難度很大。如果能利用式(13)的特點消去未知參數(B ij，σij，φij)，則能直接獲得角速度估計值[17]。下面對該估計方法進行詳細推導，其原理如圖3所示。

圖3 進動角速度估計示意圖

式中，n為離散時間值;k為距離n的步長。可得進動角速度ω的估計值為

式中 ，0＜k≤π/(σTs)。選取在一定范圍內不同的k值估計ω并求均值可以提高估計精度和穩定性。

將式(12)代入式(16)得

整理可得

式中，v=cos(ωk Ts)。可知在獲得進動角速度估計值的基礎上，上式中只有三個未知參數(a0+B i，a1，a2)。求解此方程只需要三個線性方程，即只需要在微動曲線上任意取定n1，n2，n3和k值。為了避免方程奇異，選取較長時間間隔的數據，這樣得到的結果更準確。選取一定范圍內不同的k值估計平動參數求均值可以提高估計精度和穩定性。綜上可知聯立方程(15)和方程(18)可實現進動及平動參數聯合估計。

2.3 參數估計性能分析

下面對進動頻率，平動參數估計性能進行討論。設觀測噪聲為零均值，方差為σ2ε的高斯白噪聲，則ω估計觀測方程為

則有

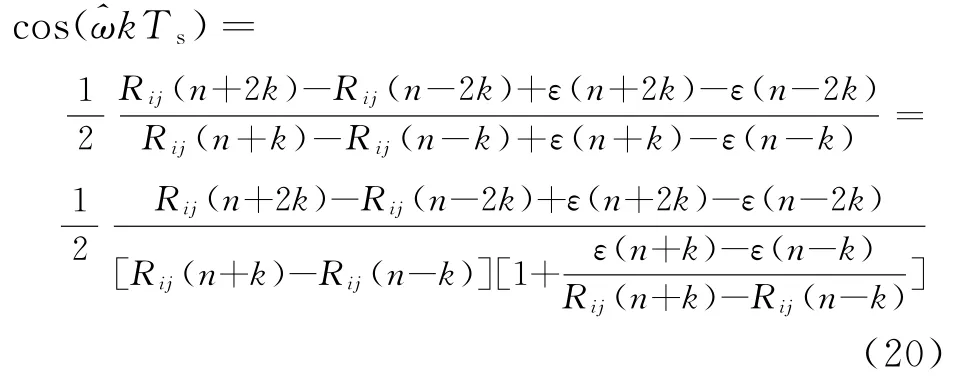
利用當x≤1時，1/(1+x)≈1-x，則上式可化簡為

E(ζ)=0，所以，由于0＜k≤π/(ωTs)，從而有，因此估計量是無偏估計量。

a1，a2參數估計觀測方程為

由式(18)可得

式中，M(n，k)=y(n+k)+ε(n+k)+y(n-k)+ε(n-k)-2(y(n)+ε(n))v，由于是無偏估計量，則估計量也是無偏估計量。

進一步還可以證明利用式(19)估計進動頻率和式(23)實現參數a1，a2聯合估計的Cramer-Rao界(CRB)分別為

在獲取平動參數的基礎上，借助傅里葉變換的移位特性完成距離包絡補償再通過相位校正[11]，進而可以得到彈道目標散射點進動引起的微距離變化曲線，具體的參數估計與平動補償的流程如圖4所示。

圖4 參數估計與平動補償流程圖

3 仿真分析

設錐體彈頭半徑為0.5 m，質心到錐頂的距離為2.2 m，到錐底的距離為0.8 m，錐旋角速度ω=8πrad/s，進動角θ=10°，雷達視線角γ=60°。初始時刻目標徑向平動速度v=6 010 m/s，徑向加速度a=6 m/s2，雷達到彈頭質心的距離R=600 100 m，相位φ=0.1 rad。初始時刻估計的平動速度^v=6 009 m/s，雷達到彈頭質心的距離^R=600 099 m。雷達發射信號時寬為128μs，載頻fc=10 GHz，帶寬B=2GHz，脈沖重復周期Ts=0.002s，回波脈沖數N=1 000，Pr=10，m1=3，q1=5，q2=60。

參數估計與平動補償結果如圖5所示，其中圖5(a)給出了回波信噪比為-6 d B時，采用距離估計值和速度估計值構造參考信號，經過解線頻調處理后得到的時間-距離像，可以觀察到其出現了周期性的消隱現象。提取其微距離變化曲線如圖5(b)所示，可以明顯看到曲線是斷續的。圖5(c)給出了回波信噪比3 d B條件下，微距離曲線經過預處理后，進動頻率f、平動參數a1和a2單次估計值隨步長k變化曲線，可知k取[10，55]時，各參數估計值精度較高且穩定，進動頻率單次估計相對誤差在5%以內，估計均值相對誤差低于0.8%，平動參數a1，a2均值估計相對誤差分別為2.63%和1.08%。這說明此方法只需1/3以上進動周期數據就能準確地估計進動頻率和平動參數，適合于利用局部微距離曲線信息完成平動補償。圖5(d)給出了k取[10，25]時，利用散射點A微距離曲線進行500蒙特卡羅仿真得到的各參數估計性能曲線。可知在3 dB以上，三個參數的估計值基本達到真實值。圖5(e)為三個參數估計值均方根誤差與CRB的最小均方根誤差隨信噪比變化曲線，可以看出較高信噪比下三個參數估計值均方根誤差均能接近CRB界，成為漸進無偏估計量。平動補償后的時間-距離像如圖5(f)所示，可見取得了較好的補償效果。綜上可知，本文所提方法適合于斷續微距離曲線參數估計，且估計精度較高、魯棒性較強。

圖5 參數估計與平動補償結果

4 結束語

彈道目標的進動導致不同時刻彈道目標相對雷達的視線角變化，使得回波幅度受調制而起伏，加上噪聲的影響，其時間-距離像會出現消隱現象。傳統滿足微距離曲線連續條件下的平動補償方法無法適用于這類情況。本文在分析彈道目標一維距離像特征的基礎上，提出一種基于斷續微距離變化曲線的彈道目標平動補償方法，在信噪比3 d B以上，進動頻率估計值相對誤差低于0.8%，平動一次與二次系數估計值相對誤差分別低于2.63%和1.08%，各參數估計值均方根誤差基本達到CRB限。盡管本文以錐體彈頭為例進行闡述，但由于其他旋轉對稱彈頭的散射點模型是一致的，因此所提方法同樣適用于其他旋轉對稱彈頭在曲線斷續條件下的平動補償。

[1]姜衛東.彈道目標電磁特征提取技術的研究進展[J].系統工程與電子技術，2010，32(10):2091-2097.

[2]莊釗文，劉永祥，黎湘.目標微動特性研究進展[J].電子學報，2007，35(3):520-525.

[3]朱玉鵬，王宏強，黎湘，等.基于一維距離像序列的空間彈道目標微動特征提取[J].宇航學報，2009，30(3):1133-1140.

[4]張海成，楊江平，王晗中.反導預警雷達目標特征識別方法[J].雷達科學與技術，2012，10(2):156-160.

[5]姚漢英，孫文峰，馬曉巖.基于高分辨距離像序列的錐柱體目標進動和結構參數估計[J].電子與信息學報，2013，35(3):537-544.

[6]艾小鋒，鄒小海，李永禎，等.基于時間 距離像分布的錐體目標進動與結構特征提取[J].電子與信息學報，2011，33(9):2083-2088.

[7]HE Si-san，ZHOU Jian-xiong，ZHAO Hong-zhong，et al.Estimating the Precession Angle of Ballistic Targets in Midcourse Based on HRRP Sequence[C]∥The 2008 IEEE Radar Conference，Rome:[s.n.]，2008:1-4.

[8]LIU Y X，LI X，ZHUANG Z W.Estimation of Micro-Motion Parameters Based on Micro-Doppler[J].IET Signal Processing，2010，4(3):213-217.

[9]ZHANG Q，YEO T S，TAN H S，et al.Imaging of a Moving Target with Rotating Parts Based on the Hough Transform[J].IEEE Trans on Geoscience and Remote Sensing，2008，46(1):291-299.

[10]楊有春，童寧寧，馮存前，等.彈道目標中段平動補償與微多普勒提取[J].宇航學報，2011，32(10):2235-2241.

[11]羅迎，柏又青，張群，等.彈道目標平動補償與微多普勒特征提取方法[J].電子與信息學報，2012，34(3):602-608.

[12]賀峰，劉承蘭，朱國富，等.基于距離和差值序列的復雜運動目標微動特征提取[J].電子學報，2012，40(3):422-428.

[13]馬梁，劉進，王濤，等.旋轉對稱目標滑動型散射中心的微Doppler特性[J].中國科學(信息科學)，2011，41(5):605-616.

[14]姚漢英，李星星，孫文峰，等.基于電磁散射數據的彈道目標寬帶回波仿真[J].系統仿真學報，2013，25(4):599-604.

[15]丁小峰，魏璽章，胡杰民，等.彈道中段目標多普勒成像算法研究[J].電子與信息學報，2009，31(12):2864-2868.

[16]陳瓊，邱峰，王俊.一種實用的多目標航跡跟蹤算法[J].火控雷達技術，2008，37(1):43-46.

[17]THAYAPARAN T，STANKOVIC L J，DAKOVIC M，et al.Micro-Doppler Parameter Estimation from a Fraction of the Period[J].IET Signal Processing，2010，4(3):201-212.