基于微分進化算法的非對稱弧齒錐齒輪約束多目標優化

錢學毅，遲建華，吳 雙

（1.武夷學院電子工程系，福建 武夷山 354300；2.大連開發區大開產業發展研究中心，遼寧 大連 116600；3.浙江經貿職業技術學院應用工程系，浙江 杭州 310018）

對弧齒錐齒輪傳動進行約束多目標優化設計是提高產品設計質量、縮短產品設計周期、提升產品市場競爭力的有效手段。傳統的格利森制弧齒錐齒輪是按照齒面兩側具有相同嚙合性能的原則進行對稱設計。但在工程實踐中，大部分傳動裝置如汽車等正轉一側齒面的使用率大大高于另一側。因此，為充分利用材料，研究弧齒錐齒輪強度的非對稱設計（在反轉齒面用一個小的壓力角、在正轉齒面使用一個較大的壓力角）即可以提高齒輪的齒根彎曲強度、齒面接觸強度和膠合強度又可以有效地避免齒頂過分變尖的現象，具有工程實用意義。文獻[1-2]提出了設計雙壓力角非對稱齒廓齒輪的思想，用以在發揮大壓力角優點的同時又可避開輪齒兩側壓力角同時增大會導致齒頂強度和柔度下降，抗沖擊能力降低，加載時容易崩齒等缺點。文獻[3]提出了在準雙曲面齒輪輪坯設計中，摒棄強度的對稱設計，修正正轉用齒面的壓力角，以增加正轉用齒面的強度，減少齒根拉應力。

本文在上述設計思想的基礎上，根據齒輪嚙合原理和現代摩擦學理論，建立了以弧齒錐齒輪傳動齒面上瞬時接觸線方向與相對滑動速度之間夾角的余切值最小、傳動總體積最小和齒面誘導法曲率主值最小為目標函數的約束多目標優化設計數學模型。借助于改進的微分進化多目標優化算法，利用MATLAB編制優化程序，通過范例對非對稱弧齒錐齒輪傳動進行兩目標和三目標優化設計。并分析了齒面上瞬時接觸線方向與相對滑動速度之間夾角及齒面誘導法曲率主值對齒面接觸強度和膠合強度的影響，為其綜合性能的進一步優化提供基礎。

1 齒面上瞬時接觸線方向與相對滑動速度之間的夾角

接觸線方向與相對運動速度之間的夾角θ在齒輪嚙合中是一個很重要的角度。它對于兩齒面在相對運動時形成潤滑油膜的條件有很大的影響。根據彈性流體動力潤滑理論中的Dowson-Higginson線接觸最小油膜厚度公式[4]

式中：hmin—最小油膜厚度(mm)

a—潤滑油的黏壓系數(MPa-1)

η0—潤滑油的動力黏度(MPa·s)

U—卷吸速度(mm/s)

R—當量曲率半徑(mm)

L—兩齒面接觸線的長度(mm)

—齒輪材料綜合彈性模量(MPa)

W—齒面間的法向載荷(N)

從上式中可見，最小彈流油膜厚度與卷吸速度（即形成油膜的有效速度）有關，卷吸速度越大，最小膜厚越大，潤滑條件越好，抗膠合能力和抗磨損能力越強。卷吸速度等于相對滑動速度在與接觸線垂直方向上的分量。因此，為了有利于形成油膜，改善潤滑條件，接觸線方向與相對運動速度之間的夾角θ應盡可能的大。依據齒輪嚙合原理

式中：α—法向壓力角(o)

β—螺旋角(o)

顯然，由式(2)計算的值cotθ越小越好。

2 弧齒錐齒輪齒面誘導法曲率主值

根據微分幾何理論和齒輪嚙合原理，兩相嚙合齒面在切點沿同一個方向的法曲率之差稱為該方向的誘導法曲率，是相對曲率，它刻劃了兩嚙合齒面在該方向上相對彎曲的程度，也就是切點沿同一方向的鄰近點相對離開的快慢程度。共軛齒面的誘導法曲率是衡量齒輪傳動質量的一個重要指標，該值越小，說明兩接觸齒面在這個方向上相對彎曲的程度越弱，當量曲率半徑越大，Hertz彈性接觸應力越小，接觸強度越高，同時Hertz應力的減小還使齒間最小油膜厚度增加，抗膠合承載能力得以提高。

過嚙合齒面上的某一切點，沿不同的方向，具有不同的誘導法曲率，必有一個最大值和一個最小值，其最大值和最小值稱為誘導法曲率主值。取得主值的方向稱為主方向，兩個主方向具有正交性。

弧齒錐齒輪在傳動時是線接觸，兩齒面在接觸線方向τ的誘導法曲率等于零，這是它的一個主方向。誘導法曲率的另一主方向與接觸線方向τ垂直，設這個方向的誘導法曲率主值為kσ，則kσ是最大值，用式(3)計算[5]：式中：σk—誘導法曲率主值(mm-1)

δ1,δ2—小輪、大輪的分度錐角(o)L1—小輪分度圓錐的錐距(mm)其他符號意義同前。

3 微分進化約束多目標優化算法

微分進化算法(Differential Dvolution, DE)是近來提出的簡單而高效的多目標進化算法，是一種采用浮點矢量編碼的全局空間中進行隨機搜索的優化算法。目前國內外對于多目標微分進化算法的研究尚處于起步階段，相關研究主要集中在算法性能的改進與完善上。國外具有代表性的有Abbass[6]的自適應Pareto微分進化算法，Madavan[7]及Xue等[8]學者的基于Pareto最優概念的多目標微分進化算法。國內的研究主要有張利彪等[9-11]學者提出的基于極大極小距離密度的多目標微分進化算法。國內外學者的研究在一定程度上提高了多目標微分進化算法的性能，但這些研究還僅限于對數學測試函數的研究，還不能直接用來進行實際工程的優化設計，尚需要進行改進。

本文在對現有的微分進化多目標優化技術進一步研究的基礎上，針對其在機械工程設計中存在的問題，提出了相應的策略，改進了現有的微分進化多目標優化技術，給出了基于微分進化技術、適用于機械工程領域的約束多目標優化算法。

3.1 現有微分進化算法在機械設計中存在的問題

機械設計中的多目標優化設計往往是在復雜而苛刻的約束條件下進行。當利用現存的算法進行迭代時，會發生下面的問題：

（1）在進行變異和交叉操作產生的新個體有可能在可行域內，也有可能在不可行域內，而支配關系的比較和極大極小距離密度的計算都是在目標函數空間中進行的，不可行域內的個體產生的目標函數完全有可能支配可行域內的個體產生的目標函數，其密度值的計算也同樣具有不確定性，這樣刪除的很可能將是有用的個體，保留的將是無用的個體。最后迭代出的結果很可能毫無意義。

（2）若變異和交叉操作只在可行域內進行，則每產生一個新個體都要進行可行性檢驗，滿足約束條件則保留，不滿足約束條件則罰掉，再重新搜索，直到滿足約束條件為止。設計實踐表明，復雜而苛刻的約束條件不但會使收斂速度慢得讓人難以接受，而且約束邊界上的目標個體還很容易使程序陷入死循環。例如，當進行齒輪設計時，若將齒數限定在20～50，當某一目標個體的齒數恰好是20或50時，用DE的變異和交叉產生新個體的操作就會使程序陷入死循環，導致優化設計無法進行。

3.2 基于極大極小距離密度實用多目標微分進化算法

為解決前述多目標微分進化算法所產生的問題，使迭代高速有效，避免程序進入死循環，提出基于極大極小距離密度實用多目標微分進化算法如下：

（1）設置初始參數：向量維度D、初始群體規模NP、縮放因子F、交叉常量CR、最終可行解規模N；

（2）在可行域內隨機生成初始群體P，規模為NP；

（3）將群體P中的非劣解加入Pareto候選解集中；

（4）在無約束條件下，用DE的變異和交叉操作，對群體P和Pareto候選解集中的每一目標個體x都生成一個新個體x′；

（5）對每一個新個體x′都進行可行性檢驗，滿足約束條件的保留，否則直接罰掉；

（6）將所有目標個體和滿足約束條件的新個體一起構成群體T；

（7）如果Pareto候選解集的規模沒有達到規定的大小，將所獲得的非劣解直接加入到Pareto候選解集中，直到達到候選解集的設定規模；否則，比較個體間的支配關系，保留支配個體，丟棄被支配個體，直到達到候選解集的規模；如果所有被支配個體都丟棄以后，候選解集的規模仍超過設定值N，則計算Pareto候選解集中每一個體的極大極小距離密度，并刪除密度值最大的個體，直到達到候選解集的設定規模；

（8）如果滿足中止條件，停止迭代，否則返回（4）。

4 范 例

非對稱弧齒錐齒輪傳動的承載能力和傳動性能與下面的兩個因素密切相關：

（1）接觸線方向與相對運動速度之間的夾角θ；

（2）齒面誘導法曲率主值。接觸線方向與相對運動速度之間的夾角θ越接近于90o，齒面誘導法曲率主值越小，承載能力越高，傳動性能越好。因此非對稱弧齒錐齒輪傳動優化設計是在滿足約束條件下尋求cotθ最小及齒面誘導法曲率主值最小，同時還要尋求齒輪傳動總體積最小（最經濟），是一個約束多目標優化問題，多目標沒有公度性，不宜用傳統的多目標優化方法來處理。這是因為傳統的多目標優化方法是將多個目標通過加權求和轉化為單目標問題進而進行優化。這樣做有以下缺點：

① cotθ無量綱，齒面誘導法曲率主值(mm-1)，總體積(mm3)，各目標單位不一致，無可比性；

② 多個目標加權值的分配帶有較大的主觀色彩，難以反映客觀真貌；

③ 優化目標僅為多個目標的加權和，優化過程中各目標的優度進展不可操作；

④ 多個目標之間通過決策變量相互制約，存在相互矛盾，致使加權目標函數的拓樸結構十分復雜。改進的微分進化技術在解決此類問題中得到成功應用。

4.1 已知數據

主動齒輪的轉速n1=960r/min，被動齒輪的轉速n2=320r/min，傳遞的功率P=100kW；選用齒輪油HL-30潤滑，其運動黏度ν100=30mm2/s；油池溫度θoil=50℃；兩輪齒面粗糙度分別為Ra1=Ra2=0.8μm。

4.2 選取向量維度D

選取7個設計變量（D=7）

式中，z1為主動輪齒數；mt為端面模數；α、β意義同前；xt為主動輪切向變位系數；x為主動輪高變位系數；b為齒輪寬度(mm)。

4.3 建立目標函數

（1）將齒輪傳動總體積最小作為一個追求的目標，即

式中，dm1、dm2分別為兩齒輪中點的分度圓直徑(mm)。

（2）將齒面上瞬時接觸線方向與相對滑動速度之間夾角的余切值最小作為第二個追求的目標，即

（3）將齒面誘導法曲率主值最小作為同時追求的第3個目標，即

4.4 確立約束條件

參照文獻[12-13]及工程實際經驗確立膠合強度約束、接觸強度和彎曲強度可靠性約束、齒頂厚約束、齒數約束、模數約束、壓力角約束、螺旋角約束、變位系數約束、齒寬約束等。

4.5 優化計算及結果遴選

用MATLAB進行程序設計計算，設置初始參數：D=7、NP=50、F=0.3、CR=0.5、N=100，循環200次，結果得到100組可行解及相應的目標函數值。以f1(X)和f2(X)為目標函數的兩目標優化非劣最優目標域如圖1所示。根據程序運行結果，從中選取2個目標函數都接近最小值，綜合性能最佳的一組結果，本例中選取圖1中左下邊界點（決策者也可根據自己的偏好選擇其他的結果）作為最終方案：X*=[z1,mt,α,β,xt,x,b]T=[12,4, 24.6202, 39.4660, 0.7541, 0.2268, 50]T，總體積V=1.5237×105mm3，齒面上瞬時接觸線方向與相對滑動速度之間夾角θ的余切值f2(X)=cotθ=2.9154，θ=18.93°。以f1(X)、f2(X)和f3(X)為目標函數的3目標優化非劣最優目標域如圖2所示。最終方案為：X*=[z1,mt,α,β,xt,x,b]T=[12, 6, 25.8226, 39.8978, 0.8567, 0.5570,17]T，總體積V=2.0980×105mm3，齒面上瞬時接觸線方向與相對滑動速度之間夾角θ的余切值f2(X)=cotθ=2.7459，θ=20.01°，齒面誘導法曲率主值f3(X)=kσ=0.0409mm-1。

圖1 兩目標優化非劣最優目標域

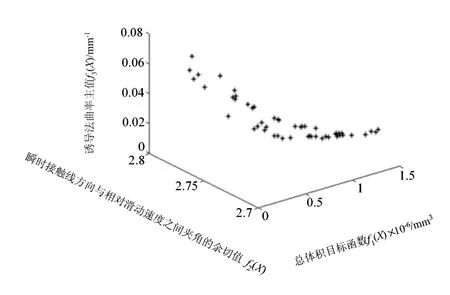
圖2 三目標優化非劣最優目標域

4.6 用粒子群算法進行優化并與微分進化算法做比較

用粒子群優化算法(particle swarm optimization, PSO)[14-15]，參照文獻[16-18]中提出的尋優原則和搜索方法對本算例進行優化。粒子群規模為100，進行200次迭代，所得非劣最優目標域如圖3所示。比較圖1和圖3可以看出，微分進化算法個體的多樣性和收斂性都好于粒子群算法。優化實踐表明，微分進化的收斂速度更是遠遠大于粒子群算法，群體規模都是100，同樣都是MATLAB編程，同一臺計算機上都是運行200次循環，微分進化僅用了35分鐘，而粒子群算法則用了20.8個小時，這是由于：

（1）粒子群算法受約束條件的限制，隨著循環次數的增加，在可行域內搜索新粒子的速度會越來越慢，而DE算法在尋求新個體的過程中不考慮約束條件，不必反復迭代；

（2）PSO算法在尋求新粒子時需要考慮粒子的歷史痕跡，而DE算法不必顧及個體進化的歷史痕跡，只需考慮當前狀態即可，相對來講，DE優化程序簡單，計算量小，PSO程序復雜，計算量大。

圖3 PSO非劣最優目標域

5 結 論

（1）本文給出了基于極大極小距離密度多目標微分進化算法的改進策略，并將改進的微分進化算法用于弧齒錐齒輪的多目標優化設計，成功地驗證了改進算法的有效性，該方法比傳統的多目標優化方法及目前常用的其他現代優化方法都具有明顯的科學合理性和實用性。

（2）本文給出的弧齒錐齒輪傳動系統多目標優化設計方法和得到的設計參數，能有效地提高產品的設計質量，提升產品的綜合經濟技術指標。該方法進一步拓展了微分進化算法的工程應用領域，對于其他復雜機械傳動系統的約束多目標優化設計也具有一定的參考價值。

[1]Litvin F L, Fuentes A, Howkins M.Designing,generation and TCA of new type of asymmetric face-gear drive with modified geometry [J].Computer Methods in Applied Mechanics and Engineering,2001, 190(43-44): 5837-5865.

[2]Difrancesco G, Marini S.Structural analysis of asymmetrical teeth: reduction of size and weight [J].Gear Technology, 1997, 14(5): 121-125.

[3]張金良, 方宗德, 鄧效忠, 吳 斌.準雙曲面齒輪強度的非對稱設計[J].機械科學與技術, 2005, 24(5):568-602.

[4]溫詩鑄, 黃 平.摩擦學原理[M].北京: 清華大學出版社, 2002: 73-75.

[5]吳序堂.齒輪嚙合原理[M].西安: 西安交通大學出版社, 2009: 293-296.

[6]Abbass H A.The self-adaptive pareto differential evolution algorithm [C]//Proc of the Congress on Evolutionary Compution (CEC’2002).Piscataway:IEEE Service Center, 2002: 831-836.

[7]Madavan N K.Multiobjective optimization using a pareto differential evolution approach [C]//Proc of the Congress on Evolution Computation (CEC’2002).Piscataway: IEEE Service Center, 2002: 1145-1150.

[8]Xue F, Sanderson A C, Graves R J.Pareto-based multi-objective differentil evolution [C]//Proc of the 2003 Congress on Evolutionary Computation(CEC’2003).Piscataway, NJ: IEEE press, 2003:862-869.

[9]張利彪, 許相莉, 馬 銘, 孫彩堂, 周春光.基于微分進化求解多目標優化問題中的退化現象[J].吉林大學學報(工學版), 2009, 39(4): 1041-1046.

[10]張利彪.基于粒子群和微分進化的優化算法研究[D].長春: 吉林大學計算機科學與技術學院, 2007:92-110.

[11]張利彪, 周春光, 馬 銘, 孫彩堂.基于極大極小距離密度的多目標微分進化算法[J].計算機研究與發展, 2007, 44(1): 177-184.

[12]秦大同, 邢子坤, 王建宏.基于動力學和可靠性的風力發電齒輪傳動系統參數優化設計[J].機械工程學報, 2008, 44(7): 24-31.

[13]齒輪手冊編委會.齒輪手冊[M].北京: 機械工業出版社, 2005: 5-9-5-134.

[14]Kennedy J, Eberhart R.Particle swarm optimization [C]//IEEE International Conference on Neural Networks:Perth, Australia.Piscataway.NJ: IEEE Service Center,1995: 1942-1948.

[15]Eberhart R, Kennedy J.A new optimizer using particle swarm theory [C]//Roc.Sixth International Symposium on Micro Machine and Human Science:Nagoya, Japan.Piscataway, NJ: IEEE Service Center,1995: 39-43.

[16]魏靜萱.解決單目標和多目標優化問題的進化算法[D].西安: 西安電子科技大學, 2009: 73-77.

[17]張 敏.約束優化和多目標優化的進化算法研究[D].合肥: 中國科學技術大學, 2008: 9-15.

[18]張利彪, 周春光, 馬 銘, 劉小華.基于粒子群算法求解多目標優化問題[J].計算機研究與發展,2004, 41(7): 1287-1290.