應用灰色模型對我國結核病死亡率進行趨勢分析及預測

李濤 成詩明 陳偉 夏愔愔 陳秋蘭 杜昕

據WHO估計，全球每年新發結核病患者880萬例，其中傳染性結核病患者390萬例，每年因結核病死亡的患者約200萬例。我國是世界上22個結核病高負擔國家之一，患者例數僅次于印度居全球第二位，結核病造成的死亡給國家和人民帶來了嚴重的危害。全國疾病監測系統死因監測(disease surveillance points, DSP)顯示，估計在我國每年有7.6 萬人死于結核病，7.2 萬人因肺結核死亡，近年來肺結核死亡在死因順位中排在第15位左右[1]，而在傳染病和寄生蟲病中死因順位排在第1位[2]。WHO發布的《控制結核病策略》中專門確立了與聯合國千年發展目標相關并由控制結核病伙伴關系通過的具體目標：到2015年，與1990年的基線相比降低50%的結核病死亡率[3]。

對于結核病的死亡影響是多因素的，建立結核病死亡率預測的多因素模型相對較為復雜；同時由于我國目前尚未建立起完善的生命登記系統，對于結核病死亡率的測算通常來源于兩種方法：一種是通過死因監測系統數據利用人口抽樣監測來估算；另一種則是通過結核病發病率和病死率來進行估算，在這種情況下獲得的死亡率數據具有模糊和不確定的特點。

灰色系統理論是一門新興橫斷學科，它以“小樣本”、“貧信息”不確定性系統為研究對象，主要通過對部分已知信息的生成、開發，提取有價值的信息，實現對系統運行規律的正確認識和確切描述，并據以進行科學預測[4]。它樣本量需求較少，在不用過多考慮相關影響因素變化的情況下，不失為一種相對簡便的趨勢研究方法，近年來在疾病監測領域有較多的應用。本研究擬通過分析近年來我國結核病歷史死亡數據，以灰色系統GM(1,1)為模型，試對我國結核病死亡率的變化趨勢進行推測，為進一步開展科學研究提供參考。

資料和方法

一、資料來源

1.全國疾病監測系統死因監測數據：2005年調整后的DSP系統，包括全國31個省(自治區、直轄市)(不含港澳臺地區)的161個監測點。其中城市監測點64個，農村監測點97個。DSP系統總監測人口8153萬，約占全國人口的6%，死因分類參照國際疾病分類標準第10版(ICD-10)[5]。本研究利用DSP系統全國2005—2012年結核病死亡率進行分析：具體見表1。

2. 《WHO全球結核病報告(2012版)》[6]估算數據：通過結核病發病率和病死率對結核病死亡率進行估算，數據結果以5年為間隔表示，因此在本研究中將5年作為時間標尺的最小單位近似擬合。本研究利用WHO報告的我國1990—2010年結核病死亡率進行分析：具體見表2。

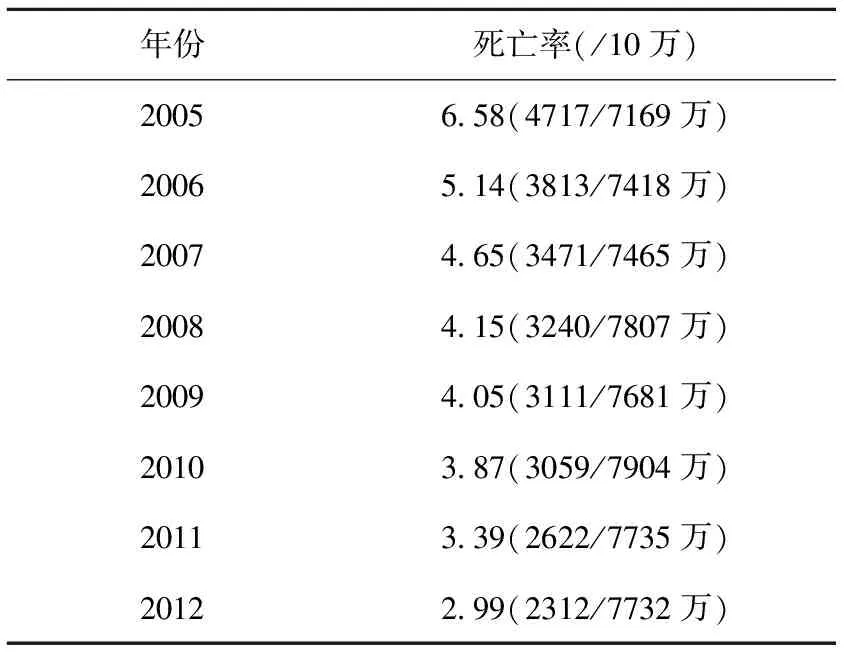
表1 全國2005—2012年結核病死亡率[2]

表2 WHO報告的我國1990—2010年結核病死亡率

二、分析方法

(一)分析原理及步驟

1.分析原理：采用GM(1，1)灰色模型處理數據。灰色模型的本質是一種指數預測模型，它通過對現有離散數據進行擬合，推出近似的差分方程，經擬合檢驗確認效果后，進行外推預測。

MATLAB 7.0是美國MathWorks公司出品的商業數學軟件，常用于算法開發，目前針對GM(1，1)灰色模型在MATLAB 7.0已經有完善的代碼模塊，直接將原始數據錄入后，計算過程在軟件中實現，輸出的數據包括差分方程(ans)、預測值(XY)、誤差值(Theta)、相對誤差值(XD_Theta)、后驗差值(C)以及小誤差概率值(P)等。

2.擬合檢驗：將預測方程的后驗差值C和小誤差概率值P與表1相比較進行檢驗，同時計算平均相對誤差值。

表3 后驗差比值和小誤差概率檢驗表

3.外推預測：如果擬合檢驗結果滿意，即模型效果滿意，則根據預測公式推算歷年全國結核病死亡率，并預測2015—2025年死亡率變化趨勢。

4.對比驗證：在SPSS 21.0中采用時間序列模型(指數平滑法)對同時期數據進行擬合預測，與灰色模型結果進行對比，檢驗預測效果。

(二)建立分析方程并擬合檢驗

1.將表1數據輸入MATLAB 7.0后獲得全國結核病死亡率趨勢模型一：

X(t+1)=-64.7458e-0.08182t+71.3258(t+1代表時間序列變量，分別對應觀測值原點開始的第1,2,3,……個年份和第1,6,11……個年份；X代表根據擬合方程以t值計算出的相應t+1年份的擬合值和預測值)。經擬合優度檢驗，后驗差C值為0.0662，小誤差概率P值為1.000，查表3得知，本模型為一級模型，模型預測精度滿足要求，可以用于外推預測。平均相對誤差為2.27%，整體擬合度好。

2.將表2數據輸入MATLAB 7.0后獲得全國結核病死亡率趨勢模型二：

X(t+1)=-38.7154e-0.40435t+57.7154

經擬合優度檢驗，后驗差C值為0．0088，小誤差概率P值為1．000，查表3得知，本模型為一級模型，模型預測精度滿足要求，可以用于外推預測。平均相對誤差為0.97%，整體擬合度好。

三、相關概念

1.差分方程(ans)：即GM(1，1)灰色模型的預測方程，通過該方程可以對原始數列進行驗算，并對新數據進行外推預測。

2.預測值(XY)：通過差分方程計算出的預測數列。

3.誤差值(Theta)：預測數列與原始數列之差(殘差)的絕對值。

4.相對誤差值(XD_Theta)：誤差值占原始值的百分比。

5.后驗差值(C)：又叫均方差比值，即殘差的方差比原始數列的方差。

6.小誤差概率值(P)：殘差與殘差平均值之差小于給定值的概率，對于給定的P0值，當P>P0時，模型為小誤差概率合格模型。

結 果

一、 利用DSP死亡率數據進行分析預測

根據模型一擬合的方程對2005—2012 年全國結核病死亡率進行預測，并做2013—2025 年結核病死亡率的外推預測，結果見表4。外推預測顯示：我國2013—2025年結核病死亡率繼續呈下降趨勢，2015年、2020年、2025年結核病死亡率分別為2.44/10萬、1.62/10萬、1.07/10萬。

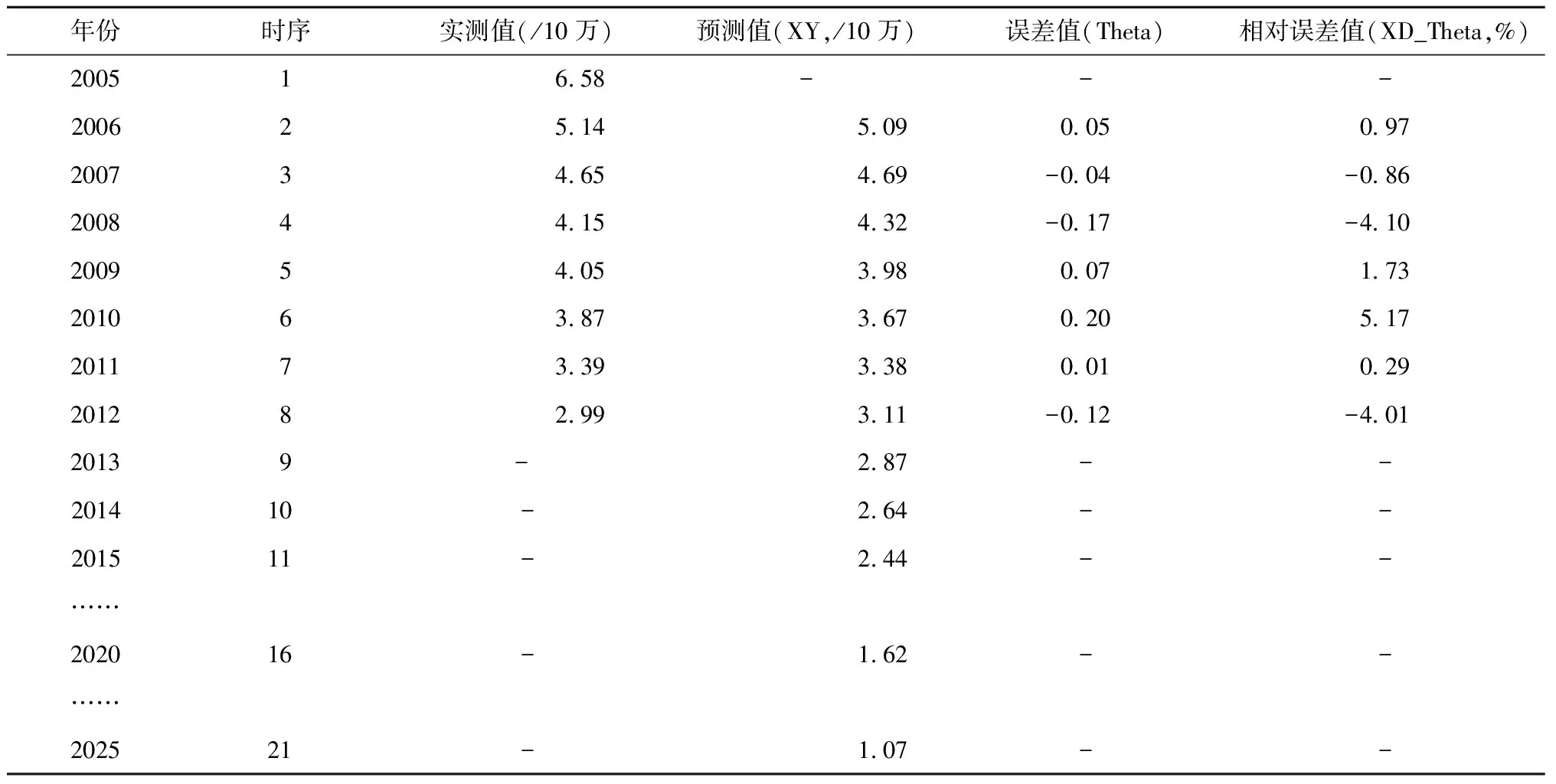
表4 2005—2025年全國結核病死亡率實測值、預測值及誤差

二、利用WHO全球結核病報告(2012版)[6]死亡率數據的分析預測

根據模型二擬合的方程對1995—2010 年全國結核病死亡率進行預測，并做2015—2025 年結核病死亡率的外推預測，結果見表5。

外推預測顯示：我國2010—2025年結核病死亡率繼續呈下降趨勢，2015年、2020年、2025年結核病死亡率分別為2.55/10萬、1.71/10萬、1.14/10萬。

三、使用時間序列模型(指數平滑法)對死亡率的擬合預測

分別將表1和表2的死亡率數據代入SPSS 21.0的時間序列模型，經多次對比擬合結果后選取指數平滑法進行擬合預測，結果見表6。

討 論

一、灰色模型用于結核病死亡率預測的可行性

對疾病死亡率的預測是一種前瞻性研究，各種方法對疾病死亡率的預測只是科學的估計，目前常用的一些預測方法(回歸分析等)，需要較大的樣本，若樣本較小，常造成較大誤差。而灰色預測模型作為一種新的數理流行病學方法，具有建模簡單、適應面廣、預測精度高、運算簡便等優點，通過少量的信息，建立數學模型，對數據進行各種處理，減少其隨機性并做出預測，對于時間序列短，統計數據少、信息不完全系統的分析與建模，具有獨特的效果。GM (1, 1)是目前使用最為廣泛的灰色預測模型，近年來在疾病預測方面得到較多運用，常用于預測疾病的發病率和死亡率等[7]。曹偉燕等[8]根據國家衛生部《2007年統計年鑒》中1998—2006年肺結核的發病率資料，建立GM (1, 1) 預測模型，顯示擬合效果較理想，并預測2007 年、2008 年、2009年全國的發病率較高，提示衛生管理部門應加強肺結核的防治工作。羅俊等[9]對武漢市1975—2006年糖尿病死亡資料進行流行病學分析，并利用灰色模型GM(1,1)預測武漢市居民糖尿病死亡率上升趨勢明顯。

二、灰色模型GM (1, 1)對現有結核病死亡數據外推預測的結果

本研究通過MATLAB 7.0軟件處理相關數據[10]，利用灰色模型GM(1, 1)分別對2005—2012年間DSP系統和1990—2010年間WHO全球結核病報告結核病死亡率數據進行擬合，經擬合優度檢驗，后驗差C值分別為0.0662和0．0088，小誤差概率P值均為1．000，模型預測精度滿足要求，平均相對誤差分別為2.27%和0.97%，整體擬合度好。在模型較為精確的條件下進行外推預測，若當前我國結核病防治工作相關環境及流行因素變化不大的情況下，我國結核病死亡率呈逐年下降的趨勢，使用兩種不同來源預測的結果基本相同，也與國內其他研究的結論相一致[11]。

三、與其他預測模型的對比

在使用WHO全球結核病報告結核病死亡率數據進行預測時，灰色模型GM(1,1)與時間序列模型(指數平滑法)兩種模型擬合度相似，平均相對誤差分別為0.97%和-0.86%，預測值也高度吻合；而在使用DSP系統數據進行預測時，灰色模型的平均相對誤差(2.27%)明顯好于時間序列模型(5.75%)，可以認為此條件下灰色模型的擬合度較時間序列模型更好。同時，由于時間序列模型在進行預測時，往往需要進行多次擬合、比對以獲得最優擬合模型，相對于灰色模型更為復雜，總體來說，灰色模型在小樣本數據的擬合預測方面，可能較時間序列模型有更為廣泛的應用。余陳斌等[12]對于鐵路施工企業矽肺的發展趨勢研究也顯示，灰色模型預測法比動態數列外推法預測精確。

表5 1990—2025年全國結核病死亡率實測值、預測值及誤差

表6 時間序列模型(指數平滑法)對1990—2025年全國結核病死亡率的擬合預測結果

四、灰色模型預測存在的問題

在使用灰色模型進行分析時，當原始數據為光滑離散數列時，利用灰色模型能得到較好的擬合和預測精度，用GM(1,1) 模型進行預測，精度較高的可能只是原始數據以后的1到2個數據，即預測時刻越遠預測的意義越弱。同時，灰色系統在發展過程中，隨著時間的推移，將會不斷地有一些隨機擾動和驅動因素進入系統，使系統的發展相繼地受其影響。因此，本研究的模型僅適用于單純考慮死亡情況，并未結合我國結核病的流行狀況和趨勢、耐藥情況，以及我國結核病防控措施的有序開展及防控效果，是在孤立、理想的狀態下進行的分析，預測結果僅適用于作為進一步深入分析研究的基本參考，實際意義可能有待進一步觀察。

五、預測結核病死亡率變化趨勢與聯合國千年發展目標

聯合國千年發展目標中要求各遏制結核病伙伴2015年要實現將結核病死亡率減少50%的目標(與1990年基線相比較)，1990年我國結核病死亡率為19/10萬，本研究中兩種數據來源的外推預測分別表明，2015年我國結核病死亡率可能會達到2.44/10萬或2.55/10萬，預計將順利完成該目標。同時，WHO在最新的結核病戰略(2016—2025)中也明確提出在2015年死亡率的基礎上到2025年，結核病死亡率再下降50%的目標[13]，外推數據顯示，我國2025年結核病死亡率可能會達到為1.07/10萬或1.15/10萬，預計也將圓滿完成該目標。但也要看到，相關資料顯示[11]，老年人口、西部地區和農村地區結核病死亡率仍然較高,需要在保證現有工作穩步推進的同時，加強結核病防治支持環境建設, 建立有效機制和衛生服務網絡促進結核病患者發現和治療管理工作，進一步降低結核病患者死亡的風險，爭取早日實現消除結核病的最終目標。

[1] 中華人民共和國衛生部. 2008 中國衛生統計年鑒. 北京: 中國協和醫科大學出版社, 2008: 268.

[2] 中國疾病預防控制中心慢性非傳染性疾病預防控制中心. 全國疾病監測系統: 死因監測數據集2012. 北京: 人民衛生出版社, 2013.

[3] World Health Orgnization. The stop TB strategy[EB/OL]. Geneva: World Health Organization, 2010 (2010-12-07) [2014-05-08]. http://www.who.int/tb/strategy/stop_tb_strategy/zh/print.html.

[4] 劉思峰,謝乃明. 灰色系統理論及其應用. 北京：科學出版社, 2008.

[5] World Health Organization. ICD-10 version: 2010[DB/OL].Geneva: World Health Organization, 2010[2014-05-08]. http://apps.who.int/classifications/icd10/browse/2010/en.

[6] World Health Organization. Global tuberculosis report 2012[M/OL]. Geneva: World Health Organization, 2012[2014-01-01]. http://www.who.int/tb/publications/global_report/archive/en/.

[7] 周霞,邱宏,王鵬，等. 灰色預測建模方法及在醫學中的應用. 數理醫藥學雜志,2007,20(1):73-75.

[8] 曹偉燕,王培承,蔡偉芹，等. GM (1, 1) 模型在我國肺結核發病率預測中的應用. 中國醫院統計,2008,15(3):211-213.

[9] 羅俊, 孫惠玲, 段紀俊，等. 1975—2006年武漢市居民糖尿病死亡率分析及預測. 中國慢性病預防與控制,2008,16(4): 343-346.

[10] 周亞非. GM(1，1)的MATLAB實現與應用. 長春師范學院學報，2012,29(1)：32-35.

[11] 胡嘉,王黎霞,陳偉，等. 中國2004—2008年結核病死亡率特征分析及趨勢. 中國防癆雜志,2011,33(4):232-237.

[12] 余陳斌, 陳子良. 鐵路施工企業矽肺發病與發展趨勢分析. 九江醫學, 2003, 18(1): 43-441.

[13] World Health Orgnization. The stop TB strategy [EB/OL]. Geneva: World Health Organization, 2006 (2007-08-16) [2014-05-08]. http://www.who.int/tb/strategy/en/.