一種新的基于Graph cuts方法的SAR圖像分割模型

劉光明，孟祥偉，楊祥紅，程 煥

（1.海軍航空工程學院a.青島校區，山東青島266041；b.電子信息工程系；c.軍事教育訓練系，山東煙臺264001；2.91967部隊，河北沙河054102）

Graph cuts方法[1]是一種快速優化技術，有效解決計算機視覺的低層次問題，如表面重構、分割、去噪等問題。其優點是迭代計算的高效性和能得到全局最優解。其缺點在于精度限于像素精度和只能用各項異性算子AO（Anisotropic Operators），不能用各項同性算子IO（Isotropic Operators）。Graph cuts方法是計算1個圖（Graph）中的最大流的方法，等價于最小割。在圖像處理問題中，圖是指像素網絡，而割（Cut）表示輪廓。圖像去噪、圖像分割等問題的能量全局最優解都可以通過求解圖的最大流或最小割問題來準確地實現。Graph cuts方法定義在最大后驗-馬爾科夫隨機場框架，是一種比模擬退火快的離散優化技術。近年來，國際上用Graph cuts方法進行圖像分割處理的研究也很深入，發表了大量的研究成果。本文對Ayed等人[2]提出的SAR圖像水平集分割模型采用Graph cuts方法優化處理，充分利用Graph cuts方法的優點，只須幾次迭代算法就可收斂，表明了算法的有效性。

1 最大流/最小割模型

在1個有向圖中，只有出去的邊沒有進來邊的節點叫做源節點s（source），只有進來的邊沒有出去的邊的節點叫做匯節點t（sink），其他的節點進來的邊和出去的邊應該是平衡的，見圖1所示。邊上有加權值，假設對于一個交通圖來說，可以認為邊上的權重為一條道路上的最大流量。對于圖中任意2個節點來說，它們之間可以存在很多路徑，每條路徑上可以承載的最大流量取決于這條路徑上權重最小的那條邊所能承載的流量，而所有路徑上所能承載流量之和就是這2個節點之間能通過的最大流。任一網絡圖（Graph）中，最大流的流量=最小割集的割量。

圖1 有向圖網絡Fig.1 Directed graph

假設G=(V,E)是1個包含1個頂點集v ∈V 和1個邊緣集e ∈E ?V×V的圖。V 包括離散圖像的所有節點和2個終端，即1個源節點s 和1個匯節點t，其余均為中間節點。E 包括圖像節點鄰域系統的所有連接（如4-連接或8-連接，見圖2所示），類似源節點s 或者匯節點t 與每個圖像節點u ∈V/{s,t}的連接。對E 中的每條邊均有權w(eij)＞0（簡記為wij，稱為邊容量），則稱這樣的賦權有向圖G為容量網絡，記為G=(V,E,w)，通過G 中邊eij的流量pij，可稱為邊eij的流量。所有邊上流量的集合p={pij}可稱為該網絡G的1個流。

圖2 圖像鄰域Fig.2 Image neighborhood

對于1個圖中的2個節點來說，如果把圖中的一些邊去掉，剛好讓它們之間無法連通，這些被去掉的邊組成的集合就叫做割，最小割就是指所有割中權重之和最小的1個割。

最大流/最小割定理（max flow/min cut theory）：對于任意1個只有1個源點和1個匯點的網絡圖來說，從源點到匯點的最大流等于最小割，見圖3所示。

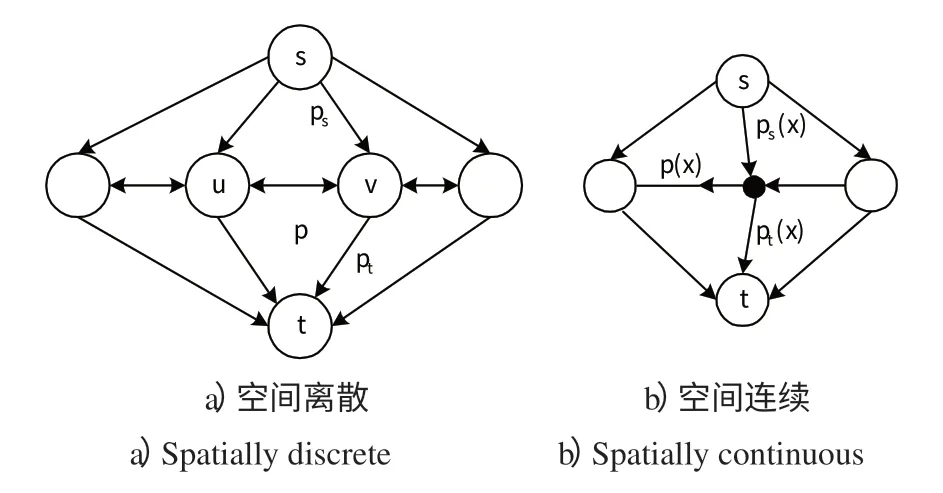
圖3 流圖Fig.3 Flow configurations

1）連續最大流模型[3]。

式（1）中：Ω為圖像域；div(?)是散度符號；ps(x)是從源點s 到點x的源流量；pt(x)是從匯點t 到點x的匯流量；p(x)是空間流量；Cs(x)、Ct(x) 和C(x)分別是與ps(x)、pt(x)和p(x)對應的約束能量。

引入函數r（對偶變量），式（1）可以轉化為與其等價的Prime-dual模型[4-5]：

2）連續最小割模型[4-5]。

對于1個圖，1個“s-t”割分割V為2個子集，即：

式（3）中：Vs包含源點s；Vt包含匯點t。

令C(e)≥0為與每個邊緣e ∈E 有關的值。每個s-t 割的能量是所有邊緣值C(e)之和，其中e ∈Est?E連接2個節點，1個在Vs中，1個在Vt中。最小割在于找到最小能量“s-t”割，即：

2 基于Graph cuts的活動輪廓模型

Graph cuts方法可以計算如下形式離散能量的精確解：

式（5）是一類一階各向異性離散二進制能量，其中，θ ＞0 和μ ＞0是系數；表示長度，表示面積。對任意(s,t)，一個次模（submodular，即最優化條件）能量滿足下式：

式（6）表明正則化項R是兩兩相互作用（3個節點間不允許有相互作用）的。

Graph cuts方法可近似求得式（7）表示的連續幾何問題的全局解為

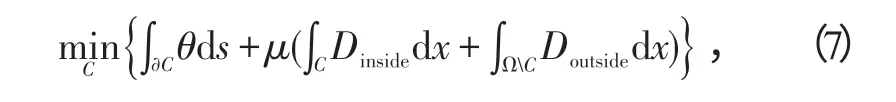
式中：C為邊緣曲線；∫?Cθds表示周長；∫CDinsidedx 和∫ΩCDoutsidedx分別表示內部、外部面積。

式（7）的近似式為

可以看出式（8）滿足次模條件。因此，Graph cuts方法可以確保取得全局最優解。

3 提出的新模型

Ayed等人提出模型[2]的能量泛函可以用變分水平集[6-10]表示為

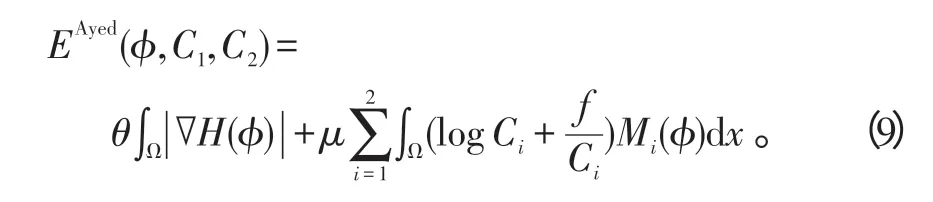
式（9）中：?是水平集函數[6]；M1=H(?)；M2=1-H(?)；ε是較小的整數；μ ＞0。

由于水平集演化方程的復雜性，還會造成計算效率較低，很難滿足實時性要求。Graph cuts方法是一種快速優化技術，其優點是迭代計算的高效性和能得到全局最優解。下面基于Graph cuts方法對方程（9）進行變換，提出圖像分割新的模型。

將圖中的節點與圖像像素相聯系，像素集的積分可以被表示為一個N×1的鏈向量，其定義為：

定義：

對于每個頂點vk和邊緣eij，其中eij可以任意分配方向。式（9）在圖（Graph）上的對應項可以簡單表示為：

對式（12）中含C1和C2的部分分別寫為：

對式（13）關于C1和C2分別求偏導數，可得到：

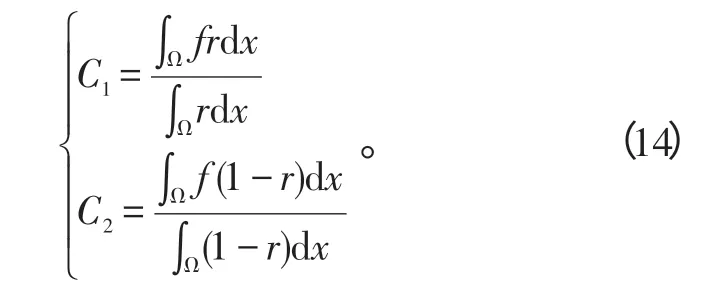
用求和形式，式（12）可寫成一個簡化的最大流/最小割計算問題：

將本文提出的新模型簡記作GC_Ayed。

算法步驟總結如下：

1）初始化C1，C2和r；

2）求式（14）得到C1，C2；

3）求式（15）中的最大流/最小割得到最有輪廓r；

4）重復步驟2）～3）直到輪廓位置保持不變為止。

4 數值實驗與分析

采用2幅實測Envisat SAR圖像來驗證和分析提出模型的分割性能，見圖4。2幅實測SAR圖像的尺寸分別為179×205 和250×250，灰度范圍為0～255。本文實驗是在CPU為AMD 1.8 GHz、內存為1 GB的硬件環境以及windows XP SP2的軟件環境下，采用Matlab 編程實現。將本文提出的GC_Ayed模型、與Ayed模型進行比較，驗證本文提出模型的有效性。

圖4 實測SAR圖像Fig.4 Real SAR images

對于SAR圖像，本文采用一種區域內部均勻性度量的方法來評估。根據圖像分割的定義，分割后圖像每個區域內部應該是均勻的，不同區域之間存在較大的差異，所以區域內部的均勻程度表征了圖像分割的質量。定義分割精度度量[11]如下：

式（16）中：Ai為圖像中的不同分割區域；C為歸一化系數；f(x)為圖像中點x 處的灰度值；ni為區域Ai中的像素個數；pp值越接近于1，表明分割圖像內部各區域越均勻，圖像的分割質量越好。

從圖5可看出，本文提出的GC_Ayed模型能準確地分割SAR圖像1中的水域，而Ayed模型不能完整地分割出水域邊緣輪廓。從圖6可以看出，GC_Ayed模型也能準確地提取SAR圖像2中的機場道路邊緣，而Ayed模型分割效果較差。從表1、2可看出，GC_Ayed模型所需運行時間大約是基于水平集的活動輪廓模型所需時間的一半，分割精度也得到了較大的提高。

圖5 SAR圖像1的分割結果Fig.5 Segmentation results of SAR image 1

圖6 SAR圖像2的分割結果Fig.6 Segmentation results of SAR image 2

表1 運行時間和分割精度的比較（SAR圖像1）Tab.1 Comparsion of running time and segmentation accuracy for SAR image 1

表2 運行時間和分割精度的比較（SAR圖像2）Tab.2 Comparsion of running time and segmentation accuracy for SAR image 2

5 結論

本文利用Graph cuts方法，將基于活動輪廓模型和水平集方法的SAR圖像分割模型轉化成最大流/最小割問題。通過實測SAR圖像的分割實驗，提出的新模型所需運行時間大約是基于水平集的活動輪廓模型所需時間的一半，分割精度也得到了較大的提高。

[1]BOYKOV Y，FUNKA-LEA G.Graph cuts and efcient nd image segmentation[J].International Journal of Computer Vision，2006，70（2）：109-131.

[2]BEN AYED I，MITICHE A，BELHADJ Z.Multiregion level set partitioning of synthetic aperture radar Images[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2005，27（5）：793-800.

[3]ZHU MINGQIANG，CHAN T F.An efficient prime dual hybrid gradient algorithm for total variation image[R].Los Angeles：University of California at Los Angeles，2008：1-29.

[4]YUAN JING，BAE EGIL，TAI XUECHENG，et al.A study on continuous max-flow and min-cut approache[C]//Computer Vision and Pattern Recognition.San Francisco，2010：1-22.

[5]PUNITHAKUMAR K，YUAN JING，BEN AYED I，et al.A convex max-flow approach to distribution based figure-ground separation[J].Journal on Imaging Sciences，2012，5（4）：1333-1354.

[6]STANLEY OSHER，JAMES A SETHIAN.Fronts propagating with curvature-dependent speed algorithms based on hamilton-Jacobi formulations[J].Journal of Computational Physics，1988，79（1）：12-49.

[7]MUMFORD D，SHAH J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics，1989，42（5）：577-685.

[8]TONY F CHAN，LUMINITA A VESE.Active contours without edges[J].IEEE Transactions on Image Processing，2001，10（2）：266-277.

[9]LUMINITA A VESE，TONY F CHAN.A multiphase level set framework for image segmentation[J].International Journal of Computer Vision，2002，50（3）：271-293.

[10]CHUNMING LI，CHIU-YEN KAO，JOHN C GORE，et al.Minimization of region-scalable fitting energy for image segmentation[J].IEEE Transactions on Image Processing，2008，17（10）：1940-1949.

[11]ROSS T D，MOSSING J C.The MSTAR evalution methodology[C]//Proceeding of SPIE.1999：705-713.